The Nature of Time: Geometry, Physics and Perception. Edited by Rosolino Buccheri, Metod Saniga, and William Mark Stuckey. Kluwer Academic Publishers: Dordrecht / Boston / London (published in cooperation with NATO Scientific Affairs Division), pp. 221-230.
© V.V.Aristov

V. V. ARISTOV

The present paper is intended to discuss how to develop the statistical approach proposed in [1, 2]. According to the relational (or relative) principle, the properties of a model clock represent the properties of physical time. (This relational view goes back to physicists and philosophers such as Leibniz, Mach, Einstein, Poincare, et al.) To construct a model of physical time implies constructing a model instrument for its measurement, namely, a clock. In the postulated basic equation, the increment of time is expressed through the average value of increments of spatial coordinates of particles of the system under consideration, and time and space are closely connected. The relationships correspond to conservation laws, and the standard motion equations are derived from this basic correspondence.

Thus the nature of physical time is treated in a constructive manner: one should consider time as a dependent variable. In the model, the passage of time is reduced to a concept at a deeper but less distinct level, namely motion. A simple perception (more precisely, simple observations of the motion inherent to every clock) leads to the first elementary conclusion about the relative character of physical time. Motion which is intrinsic to a physical clock can be described by spatial displacements. The displacement is determined by a pair of “close pictures” (moments of time). Each moment of time is a pure spatial picture. (In so doing, one may introduce the notion of a “now”, so this model is more general than the traditional theory). In fact, “elimination of time” is achieved, because time is reduced to spatial description.

By constructing a mathematical model of a clock, we also attempt to understand the origin of the mathematical form of physical laws. This form depends on the mathematical equations inherent to the fundamental instruments with the given structure. The ordinary physical equations are the consequences of the mathematical axioms, which are “projected” onto physical reality by means of the fundamental instruments. One may assume that it is possible to construct different clocks with different structure, and in this case we would have different equations for the description of motion.

In the present paper the relational approach is developed by constructing a model of rods (rigid rulers). A model geometry of physical space is produced. Being combined with the model of time, it forms a model of space-time in dimensionless variables. Attention is also paid to quantum effects appearing in the statistical discrete relational method, where the geometrical construction is based on a graph formalism reflecting the discrete atomic structure of a rigid rod.

We construct a model clock. (One might introduce a new term “temporometer”, because properties of this theoretical instrument are broader than those of a traditional clock). A moment of time (the instant, the “present”, the “now”) is defined in the following way. We consider a system which consists of particles. (The world with its atoms is an example of such a system). We assume that there is an “ideal camera” which can obtain “pictures” (snapshots) of all the particles of the system under consideration. A frame of reference is constructed. A Cartesian coordinate system is defined for this frame. Radius vectors of particles are determined by the “picture”, where particles are seen near the appropriate coordinate positions of the coordinate system. Let a point in the configuration space be , where is a radius vector, and is the number of particles of the system). The geometry of relational time is complicated: the moment of time is now characterized not by a single point on the time axis, but by a point in 3N-dimensional configuration space, i.e. by the radius vector in this space. A passage of time may be introduced if we consider a series of “pictures”. An increment of time is obtained by infinitesimal increments of the coordinates of particles: , being an increment of the radius vector, for , where the superscripts (1) and (2) index the “pictures”. The basic equation of the model time is written in the following way. The motion of “the hand of a clock” represents the uniform, uninterrupted and one-directional character of the flow of time. We introduce the equation for a time increment in which the set of all particles of the system simulates these properties:

. (1)
A motion in the system under consideration is characterized by a point in 6N-dimensional phase space. After definition of velocities of particles , we may consider 6N-dimensional phase space with points , where .

We describe schematically how (according to the correspondence principle) we derive the ordinary kinematic and dynamic relationships starting from Eq. (1). First, we have invariance of under the translation transformation, i.e.

with ,

where is related to a particle under consideration For the nonrelativistic case all points may be connected by a common light signal (without retardation). This leads to the Galilean transformation with as the absolute time:

and , where .

In the relativistic case we model the proper time, all coordinate increments obtained by the camera in the proper system being related to by a formula similar to (1). All coordinate increments in “the laboratory system” are computed by the formulae , and the model time in “the laboratory system” is found by Eq. (1), (). Time is no longer absolute. The relativistic time in the laboratory system, taking into account the retardation of a light signal, has the following form:

,

We obtain the relations

Thus the laboratory system velocity is bounded, and a constant can be associated with the speed of light in a vacuum The Lorentz transformations can be deduced easily from the above formulae. Note from (1) that the average velocity is equal to . Of course, this does not contradict relativity theory. Indeed, time in Eq. (1) and in the proper system is determined by moments at the same space point. The relativistic time in the laboratory system is determined by measurements at two different points (Einstein’s synchronization).

The basic equation (1) provides analogues of the motion equations of mechanics for the classical and relativistic cases (see [1,2]). From (1), for a system consisting of particles, we obtain after obvious transformations

(2)

where is an arbitrary factor with the dimension of mass, e.g. of a nucleon. According to Mach’s principle the right-hand side of (2) without a factor can be treated as “a force potential”. (For the inertial mass of the system of particles of equal velocities we have , i.e. a mass expressed through integers is obtained in “kinematic fashion”). For a closed system of particles (with defined inertial frame) we have a conservation of kinetic energy. In accordance with the translation invariance of (1), the appropriate infinitesimal operators of the given group provide the equation of momentum conservation. Equations similar to the dynamics equations of special relativity can be derived.

3. Relational Statistical Model of Space

In order to generalize the space-time concept, we intend to construct a relative scheme of space as a configuration of particles (“space-matter”, “space-mass”). The discrete structure of the physical space is directly related (at atomic scales) to the discrete structure of the matter. Comparing units of space and mass, we attempt to construct a model for a dimensionless description of “mass-space-time”.

The recent interest in complex geometric models at the Planck scales is well-known. One might mention the concept christened “foam” by Wheeler (see, e.g. [3]) in which space-time is highly curved with all possible topologies on the scales of the Planck length. This space-time appears smooth and nearly flat on large length scales. Therefore it cannot be directly used on atomic scales (although it provides an interesting geometric model). In our opinion, we should first consider atomic-order scales at which quantum phenomena appear. We try to describe non-determinism as a manifestation of space-time itself. The physical geometry could be treated as a geometry which differs from ordinary Euclidean geometry. Usually geometric notions arise from continuous figures. In contrast, the statistical approach implies that continuous Euclidean geometry is a limit of a more general geometry originating from simple physical figures. (The idea of the method is outlined in [4]). In this statistical geometry, the macroscopic physical distance indirectly involves a summation with the use of macroscopic instruments for spatial measurements. A rod is considered as a piece of uniform matter consisting of atoms. The rod is placed alongside the object under measurement, so the particles of the rod are related to particles of the object. At small distances the number of particles is small and there are statistical fluctuations. In geometric terms this means that we “observe” a discrete structure. The length is determined by the operation of correlation with the particles on the straight line of a rod (defined as a shortest path on a graph). A straight line may be non-unique, and we are lead to a version of non-Euclidean geometry.

The formalism of graphs is applied. Particles are naturally related to vertices of graphs. To introduce edges of the graphs, one should make a principal physical statement. The sequence of particles of the uniform medium is used in the above-mentioned operation where particles of the rod are related to particles of the object. To construct the sequence of particles, a chain of vertices is used. We can introduce a notion of adjacency (neighbourhood) of particles and a notion of adjacency of vertices is defined. A pair of neighbouring vertices provides an edge of the graph. Due to symmetry we consider a simple, non-orientable, connected, denumerable, regular graph. We study all paths between vertices A and B and count the number of vertices on all possible paths and find the minimum. By definition any path minimizing this number represents a segment AB of a straight line. А distance is expressed through this number and we denote it as . We cannot measure a distance less than “one particle”. Hence there is a minimum length

(3)

of the order of an elementary particle, being the mass of the particle and a factor expressed using fundamental constants. One can express a distance by integer multiples of the unit of mass.

Construction of a geometry is developed according to the axiomatic formalism similar to the well-known Hilbert axioms. In such an approach, axiomatic concepts of points, straight lines and planes are introduced first. In our geometric scheme, we respectively consider points (vertices), straight lines constructed on the graph, and planes constructed on the basis of vertices and straight lines. (An extension of a segment AB of a straight line outside the boundary points A and B is defined but for the sake of brevity we do not describe this procedure). A plane is determined through three points which do not lie on the same straight line. Let us take such points A, B and C. We take an arbitrary point D. If D lies on AB or BC or AC, then D lies on the plane ABC by definition. If not, we draw the straight line DF, where F is a point lying on one of the three basic straight lines, e.g., on AC. If DF intersects one of other straight lines (AB or BC), then we say that D lies on the plane ABC, and otherwise not. The set of points D with such properties forms the plane ABC.

We briefly consider the axiomatic system (some of these statements may be deduced in the framework of our model). There are five groups of axioms. I. Incidence axioms (8 axioms): all axioms are valid excluding : “There exists exactly one straight line intersecting two points”. II. Order axioms (5 axioms): all axioms are valid. III. Congruence axioms (8 axioms): all axioms are valid. IV. Continuity axioms (2 axioms): all axioms are valid. V. Axiom of parallel lines: the statement may be invalid because of the non-uniqueness of straight lines, and also because of possible general relativity effects (note that in the present paper these effects are not studied).

Let us consider a graph structure of straight lines and a possible transition to macroscopic (Euclidean) geometry. We suppose that there is a set of segments AB of appropriate straight lines AB. All these segments have length . The total number of these segments is equal to . Let a “cross-section” of these segments AB at a distance be a set of vertices situated at the same distance from A. The number of segments intersecting each cross section is constant, and is equal to .

Now we consider vertices for a fixed cross-section situated at a distance from A. Let be the number of segments intersecting a vertex C. We may treat a value as a probability that a segment AB intersects the given cross-section in a point C. Let us consider a vertex E for which the probability is maximal. Consider a straight line (in the given cross-section) which intersects the point E. Let the distance in this cross-section between a point E and an arbitrary point C be . We may attribute a probability to this coordinate . One obtains a mean value and variance. The variance of this random distribution (if it exists) could characterize the thickness of the tube formed by the segments AB. Let be the maximum of the variances of the distributions for all straight lines intersecting the point E.

The unique segment of Euclidean geometry may be obtained if the ratio of the thickness to the distance between A and B tends to zero for macroscopic lengths. More precisely, the main definition is as follows: passage to the limit of Euclidean geometry is valid if , where is the maximum of the variances over cross-sections for all .

To illustrate this passage we cite an example of the statistical calculus of a graph with simple incidence properties. For a regular graph, the degree (the number of edges with which a vertex is incident) is a constant. Let us consider a graph with even degree, i.e., . The number of segments AB is equal to the multinomial number . A similar combinatorial task is considered, e.g., in [5], where the number of paths following the direction of the arrows going from A to B is found (a lattice of q-tuples is introduced for description of the graph). For this regular graph it is possible to introduce a coordinate system.

Let us consider this calculus for the simplest case . If the two-dimensional coordinates of a point A are , and of a point B are , then the distance between the points A and B is . And is the number of segments AB. Here are binomial coefficients. The aforementioned probability for a point C with coordinates , where , is given as follows: . For a simple illustration we consider the case (a “rhombus”). The probability in this case takes the form Let us consider vertices with coordinates for the fixed cross-section situated at the distance from a point A (). The flux of segments AB intersecting any cross-section is a constant, and is equal to . For the probability distribution in this cross-section we have (applying the well-known combinatorial relationships)

We expect to obtain a maximum of variance over cross-sections if we consider the case . In this case . After introducing a centered variable (similar to the above coordinate ) and using the known approximation for (see, e.g. [6]) we obtain . The Stirling formula gives . Hence ). Thus the condition for the transition to Euclidean geometry is valid because .

4. The Uncertainty Relation in the Relational Model of Space-Time

Quantum effects may be connected with the fact that the relative concept imposes limits on the precision of measurements of space and time. Taking into account (3) we find for the position increment of any physical coordinate : . As time is a dependent variable, there is a restriction on the time increment. We consider the basic equation (1) written for finite but small values . Using the restrictions we get 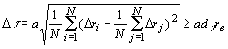, where the factor (we use a natural assumption concerning random distributions of vectors which are not equal to an average value ).

An analogue of the uncertainty relation can be deduced if we evaluate the minimum of a product of increments of coordinate and velocity. The velocity of a particle cannot be computed as a usual limit when increments of coordinate and time tend to zero, namely . This limit condition implies that the moduli of increments of all particles tend to the same value . So is of the order of , because for an estimation of the relative error of the velocity we have . Thus (recall that is the mean square velocity that is a consequence of Eq. (1)). As a result we have for a free particle

If we assume equality of this value and the Planck constant, we find or The last formula corresponds to the Compton length and if, for example, we assume that is the mass of a nucleon, then (to an accuracy of a few orders ) equals the diameter of a nucleon, a constant At microscopic scales the notion of the trajectory of a particle loses its meaning because of the non-uniqueness of straight lines, and because differentiable curves are eliminated. To illustrate non-determinism we consider the free motion of a particle. Besides the standard equation we have a second equation because we deal with finite-differences:

.

Here we formally suggest that there exist appropriate derivatives (for non-differentiable values such derivatives should be treated as some average quantities).

We see that there are additional terms in the motion equations. In particular, the Hamilton-Jacobi equation can be deduced with an additional term of the order of the Planck constant . One may attempt to derive the Schrödinger equation using recent models where the equations of quantum mechanics are derived from diffusion equations with additional terms [7] or from a fractal space-time model [8]. In the framework of the relational concept these additional terms appear as a consequence of the basic equation.

We outline some ways of developing the relational statistical approach. The notion of irreversible time could be introduced on the basis of the complex character of the geometry of relational time. One of the reasons for introducing the above model of space, where distance is measured in units of mass, is that one may deduce the universal distance force potential equation. We can compare two dimensionless sums: the first from the right-hand side of Eq. (2), and the second being If there are two random distributions of velocities and masses in the world, we can compare these two sums by means of the theorems of probability theory. One might also expect to explain the so-called cosmological coincidences in which the microcosm is linked to the macrocosm in terms of mathematical relations. (This important issue was discussed in [9]. See also the recent work [10]). The statistical theory of space-time, in our opinion, is capable of dealing with such large numbers as the Eddington number , i.e. the number of nucleons in the metagalaxy. In [1,2] it was supposed that there are very small differences in the masses of the particles of one class (the relative accuracy is ~ ), and we expect that there are other effects of order .

I am extremely grateful to Prof. Jonathan Smith for a careful proofreading of the manuscript.

1. Aristov, V.V. (1994) Statistical model of clocks in a physical theory, Physics-Doklady (Doklady of the Russian Academy of Sciences) 39, 45–48.

2. Aristov, V.V. (1995) Relative statistical model of clocks and physical properties of time, in A.P. Levich (ed.), On the Way to Understanding the Time Phenomenon: the Constructions of Time in Natural Science, World Scientific, Singapore, pp. 26–45.

3. Hawking, S.W. (1978) Spacetime foam, Nuclear Physics B144, 349–362.

4. Aristov, V.V. (1999) Statistical mechanics and a model for description of space-time, Communications in Applied Mathematics, Computing Center of the Russian Academy of Sciences, Moscow (in Russian).

5. Berge, C. (1971) Principles of Combinatorics, Academic Press, New York and London.

6. Kittel, C. (1973) Thermal Physics, Wiley, New York.

7. Nelson, E. (1995) Quantum Fluctuations, Princeton University Press, Princeton.

8. Ord, G.N. (1996) Fractal spacetime and the statistical mechanics of random walks, Chaos, Solitons and Fractals 7, 821–843.

9. Eddington, A. (1949) Fundamental theory. Cambridge University Press. Cambridge.

10. Kafatos, M., Roy, S., and Amoroso, R. L. (2000) Scaling in cosmology and the arrow of time, in R. Buccheri, V. Di Gesù and M. Saniga (eds.), Studies on the Structure of Time: From Physics to Psycho(patho)logy, Kluwer Academic / Plenum Publishers, New York, pp. 191–200.