 . (1)
. (1)RELATIVE STATISTICAL MODEL OF CLOCKS AND PHYSICAL PROPERTIES OF TIME
V. V. Aristov
1. About relative concept of time
The theoretical model of clocks and the appropriate model of time associated with it is described. The average motion of all particles of the system is taken into account. The treatment of time as a measure of motion is one of the traditional approaches to understand the nature of time. We will not observe the historical aspects of this problem (the literature is very wide). One can note only that this concept has been confirmed by the new physical theories and above all relativity theory.
Space-time in relativity theory has the four-dimensional status due to the fundamental character of the speed of light. However the analysis of measuring space and time allows to set the problem: could these two different procedures be connected in one manner (of course in different functions)? Namely "time" in this approach could be the function of values measured by rods. This equation will be the basis of the theory in which the analogs of known kinematic and dynamic relationships will be constructed.
This approach, it seems, is similar to the Mach principle treated here as the philosophical statement about the connection between space-time and motion of physical bodies (formulation of inertial properties in the Mach principle is given in 3). In any case in our constructions the view that time passes because there are moving bodies is realized.
Some physicists and philosophers noted the importance of modelling of clocks and rods, let us consider only several remarks of known authors.
A.Einstein (1949): "...strictly speaking measuring rods and clocks would have to be represented as solutions of the basic equations (objects consisting of moving atomic configurations), not, as it were, as theoretically self-sufficient entities. However, the procedure justifies itself because it was clear from the very beginning that the postulates of the theory are not strong enough to deduce from them sufficiently complete equations for physical events sufficiently free from arbitrariness, in order to base upon such a foundation a theory of measuring rods and clocks. If one did not wish to forego a physical interpretation of the coordinates in general (something which, in itself, would be possible), it was better to permit such inconsistency with the obligation, however, of eliminating it at a later stage of the theory".
A.Poincaré (1913) proposed that space is amorphous, loose solidness form, which could be applied to all indiscriminately; it does not have any properties of its own. To engage on geometry it means to study properties of our instruments, i.e. properties of a solid body. These notions concerning space are applied to time too.
W.Pauli (1956): "I think it could not be very difficult to construct a model of clocks if the existance of matter would be put in mathematical terms of the theory. It seems that it would not be an arbitrary system because the clock model have to measure the proper time ds2."
Last time some possible theoretical concepts of space-time have been discussed. For example E.Zimmerman assumed that space-time arises due to particle counteractions. It is applicable only to macroscopic objects likewise thermodynamics quantities. However no mathematical model has been proposed.
In our constructions a clock pace shall be modelled as a function depending on motion of a very large number of particles (the limiting number could be chosen equal to the Eddington number of nucleons in the metagalaxy, that is approximately 1080 ).
Such notions on clock properties (hence, and the physical time) are associated with real motion of a certain physical objects in every ordinary clock. It may be the sun, a hand of a clock and so on. However, a clock pace must not be connected with a motion of an arbitrary choosing body, because it, for instance, could be stopped relative to the fixed frame of reference. The usual point of view treats a clock pace as the uninterrupted and the equable one. The equability is the property of uniformity of a time course realized by a clock. It is supposed that the ideal clock have to work uninterruptedly. Of course a certain clock can be stopped but "a sum" of all clocks (and of all moving objects) have to model a time course. The equability is the property understood intuitively (this problem will be discussed in details in 6.). Both mentioned properties could be satisfied if we consider an averaged motion of N particles belonging to the given system, which would model "the sum" of the particle motion in the world. Every particle movement will be defined as space displacement between two "experiments" without regard to time itself.
The present model deals with random particle motions in contrast to the traditional physical clock's model constructed by using periodical processes. A large number particle averaging results in small differences between the model theory and the traditional one. A statistical error depends on the particle number, therefore the model corresponds to the traditional theory when the particle number tends to infinity. From our point of view the usually emphasized periodical property of clocks is a secondary one permitted to define conveniently a time unity. The property of equability of clock's pace (temporal equability) is more important. And a clock pace has a "historical" character, because a pace of clock's standards was corrected permanently by arranging the motion of astronomical and another objects.
A time interval between two "experiments" in which space positions are fixed, is defined as a mean square of differentials of all particle radius vectors. The distinguishing feature of the model is the use of some integral characteristic covering all particles in the system. On the other hand it is important that a time interval is defined for infinitesimal displacements of all particles. It means that the integral and the differential characteristics appear in the unified equation.
On the basis of this equation the Galilean transformations and analogs of the dynamics equations are derived. The relativistic generalization is found. The possible distinctions from the traditional theory due to statisticity of the model are investigated.
For the present model the quantitative expression of the statement that time is a measure of changes of system states is given. The state is treated as a set of all particle coordinates. And the instant of the model time is now not the point on the time axis but the point in the 3N-dimensional configuration space. Conclusions about the properties of physical time can be deduced, in particular to consider a problem on irreversibility of time.
In the last paragraph prospects of this concept are discussed. Apart from "the world time" a construction "the internal time" for a subsystem with the number of particles less than that in the whole system. Such conversion of times constitutes a sort of hierarchy. The possible generalizations connected with the creation of other types of clocks are also discussed.
2. The basic definitions of the model and obtaining the classical kinematic relationships
For construction of a classical clock the system of N identical particles (atoms) is considered. Time will be determined by motion of all particles under consideration. The motion is specified by changes of spatial positions of particles in a given reference frame.
It is well known that as a rule a geometrical frame of reference supplemented by a clock is denoted as a frame of reference. (A continuum of geometrical points with fixed distances between them is denoted as a geometrical solid media which is taken as a geometrical frame of reference.) Let us consider the system of particles at rest (the term "at rest" will be defined later). They have numbers from 1 to L (it is supposed that all particles may be labeled). Such discrete system will be an approximation for abstract continual solid media. In proposal model time is not an original quantity therefore a clock is not an original element of reference frame.
Let us define spatial displacement (motion) of particles. It is supposed that there is a physical signal (light) whereby all spatial points can be connected. In every point of space (for a given references frame the coordinate system is introduced) the ideal device ("a camera") is placed. One can obtain "pictures", e.g. note positions of all particles of the world. If mutual position of several particles (for instance with numbers 1, ..., L) on different "pictures" does not vary, then such group of particles is said to be "motionless". By using this "unmoved body" the reference frame is, in fact, introduced.
Assume that Cartesian coordinates in a given reference frame are introduced. Then in "pictures" one can fix positions of all world particles near coordinate markers. Therefore there is the correspondence between the particles and coordinate markers at a given "picture". A set of radius vectors of all particles obtained by "the camera" will be named "experiment". If "the camera" is situated at the point A, the "experiment" is
R
(A)At first the classical nonrelativistic situation will be considered. It is supposed that there is the universal light signal, i.e. all points of reference frame could be connected by this signal and all "pictures" will be identical (from the viewpoint of the relative positions of the particles).
It is natural to refer all these "pictures" to the same moment of the model time. Therefore one can use in a given reference frame only the single "camera" situated, e.g., at the origin of the coordinates. (This situation is analogous to the classical one where the reference frame can be supplemented by the single clock spaced at the origin.)
Let us introduce the model time t (a correspondence of this theoretical time to time measured by an ordinary physical clock will be discussed in 6.). Let us suppose that the value of the time interval dt is the function of differences of spatial positions (for all particles). The desired properties for this function could be formulated in advance:
1) it is required of dt that it equals to zero if all arguments are equal to zero;
2) it is non-negative at every argument value that is consistent with the preposition about time flow which has one direction (the problem of irreversible time will be discussed in 6.);
3) it is symmetrical for all arguments;
Consider two "experiments":
R
(1)(A)={Let us suppose that particles have been displaced on infinitesimal distances between two "experiments", i. e.
d
The time interval dt which has passed between these two "experiments" is defined in such manner:
 . (1)
. (1)
The possibility of motion of every particle "there and back" is excluded due to the fact that all movements are infinitesimal (for this purpose one have to push the button of "the camera" sufficiently rapidly). Otherwise dt2(A) could be zero if all particles reverted to the initial positions up to the second "experiment".
Note that the quantity dt2(A) is equal to zero when all values d![]() i(A) are equal to the mean value
i(A) are equal to the mean value ![]() , i.e. in the case when all movements are identical. In principle one could consider this fact as natural restrictions of the model: time doesn't pass if the world moves as undivided object. However this case is not realized under our assumption because there are L unmoved particles with respect to another ("unmoved body"); then one can see that dt is not equal to zero (if only all other particles are not at rest with respect to a given L particles).
, i.e. in the case when all movements are identical. In principle one could consider this fact as natural restrictions of the model: time doesn't pass if the world moves as undivided object. However this case is not realized under our assumption because there are L unmoved particles with respect to another ("unmoved body"); then one can see that dt is not equal to zero (if only all other particles are not at rest with respect to a given L particles).
The sign (A) marked the point where "the camera" is placed, could be reduced accordingly to previous argumentation. Let us assume that a multiplier a is a constant. For nonrelativistic approximation this quantity is only the coefficient (with the dimension of ratio of time on distance). In the relativistic case a is connected with the velocity of light (see 5.).
The velocity of every particle is determined naturally
![]() . (2)
. (2)
It follows immediately from (1) and (2) that
 . (3)
. (3)
Thus the quantity 1/a is equal to the mean square velocity of all particles.
The form of the model time interval according to Eq. 1 is justified by subtracting the value 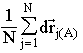 characterising a motion of the center of mass leading to the time interval dt2 which describes the sum of "chaotic part" of N moving particles. This statistical sum is analogous to the expression for a temperature in the kinetic theory of gases. But an essential difference is obvious, because there are infinitesimal quantities in Eq. 1. And there is an integral value (the sum) on the right-hand side of Eq. 1, of course one can try to transform this sum into appropriate integral.
characterising a motion of the center of mass leading to the time interval dt2 which describes the sum of "chaotic part" of N moving particles. This statistical sum is analogous to the expression for a temperature in the kinetic theory of gases. But an essential difference is obvious, because there are infinitesimal quantities in Eq. 1. And there is an integral value (the sum) on the right-hand side of Eq. 1, of course one can try to transform this sum into appropriate integral.
Now the kinematic relationships will be obtained. Let us consider the translational motion of one reference frame relative to the other. Let us suppose that images of particles on "pictures" will coincide at two close points A and A' in two different reference frames. This natural assumption is in agreement with the classical view about the existence of the universal light signal. But the coordinate markers for these images in different frames will be different (because coordinates of A and A' in their reference frames are different in general ). And this difference for all coordinate markers is equal to the difference between A and A' coordinates.
Let us consider two reference frames moving translationally one related to another. The first "experiments" are made when origins are in line. Then
R
(1)(O)={where O and O' are origins of "laboratory" and "primed" reference frames respectively. The second "experiments" are obtained when the point O' is displaced relatively to the point O and is located near the point A of the "laboratory" reference frame. We have
R
(2)(O)={According to the existence of the universal light signal "experiments" the times at the points A and O obtained at this moment are identical, i.e.
![]() (2)i(O) =
(2)i(O) = ![]() (2)i(A) , i =1, ..., N.
(2)i(A) , i =1, ..., N.
The difference between the coordinate markers obtained in the second "experiment" for the "primed" reference frame and coordinate markers of the "laboratory" frame is equal to the displacement of the point A from the point O. This displacement is equal to
d
Here ![]() (1)O(O) is the radius vector of the point O, determined in the first "experiment" (
(1)O(O) is the radius vector of the point O, determined in the first "experiment" (![]() (1)O(O) = 0 because the point O is the origin of the coordinates),
(1)O(O) = 0 because the point O is the origin of the coordinates), ![]() (2)A(O) is the radius vector of the point A, which is determined in the second "experiment". Then
(2)A(O) is the radius vector of the point A, which is determined in the second "experiment". Then
![]() '(2)i(O')=
'(2)i(O')= ![]() (2)i(O) - d
(2)i(O) - d![]() (AO) , i=1, ..., N.
(AO) , i=1, ..., N.
After subtracting the value ![]() '(1)i(O') from the left-hand side of this equality and
'(1)i(O') from the left-hand side of this equality and ![]() (1)i(O) analogously from the right-hand side, one has relationships between displacements of radius vectors
(1)i(O) analogously from the right-hand side, one has relationships between displacements of radius vectors
d
where d![]() 'i(O') =
'i(O') = ![]() '(2)i(O') -
'(2)i(O') - ![]() '(1)i(O') , d
'(1)i(O') , d![]() i(O) =
i(O) = ![]() (2)i(O) -
(2)i(O) - ![]() (1)i(O) .
(1)i(O) .
The expression for dt'(O') is analogous to Eq. 1:
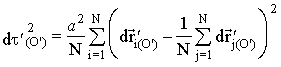 . (4)
. (4)
Substituting Eq. 4 into the right-hand side of this equality we have

It denotes that
d
t'(O')=dt(O) . (5) The quantity 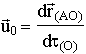 is the velocity of the origin of "primed" reference frame (or the velocity of a particle connected with it). Therefore, Eq. 4 is the Galilean transformation, which can be written in the usual form:
is the velocity of the origin of "primed" reference frame (or the velocity of a particle connected with it). Therefore, Eq. 4 is the Galilean transformation, which can be written in the usual form:
d
It is of importance that the Galilean group is not postulated now, but is contained in Eq. 1. The transformations for velocities are (as consequences of Eq. 5 and Eq. 6):
![]() '
'
These transformations are valid for all reference frames moving at least translationally relative to each other (it is not necessary with constant velocity). Concept of the inertial system is not defined yet. Let us formulate the criterion defined the inertial reference frame. Find the connection between the proposed mathematical relationships and equations of dynamics of Newton's mechanics.
3. Obtaining the relationships of dynamics in the model
Eq. 1 is the basis for deriving analogs of the conservation laws and equations of motion (it would be more correctly to denote these consequences not as "conservation laws" because they are theorems now). Let us introduce the conditions which define the inertial reference frame.
The global characteristic of all particles appears in Eq. 1 for the model time interval. Therefore, it is natural to expect that the definition of the inertial system is concerned with the Mach principle.
After simple transformations on the right-hand side of Eq. 3 we obtain
 .
.
Let us study now the dynamic properties of a system of M particles. Rewrite the last equality as follows:
 . (8)
. (8)
The inertial properties of the given frame of reference will be determined through the dynamic characteristics of N-M particles (or through the dynamic characteristics of M particles that is the traditional approach to determine the inertial properties). And the criterion of inertiality of the reference frame will be formulated.
Recall that the reference frame of the given model consists of "unmoved body" of some L particles and "moving body" (i.e. all particles moved relative to "unmoved body"). Whether the reference frame can be named inertial or not depends on the character of the particles motion relative to the "unmoved body". If the other set of particles is chosen as "unmoved body" (e.g. with numbers L+1, ..., L1) the motion of N-M particles relative to the novel "unmoved body" can have other properties. As a consequence the novel reference frame can alter the inertial properties itself.
The group properties of relationship under consideration can be used to derive the equation for the vector measure (momentum) from the equation for the scalar measure of motion (kinetic energy). It is known that if a function is invariant under some continuous transformation then it is governed by the equations prescribed in terms of the infinitesimal operators. In our case such group is the three-parametric Galilean group, hence there are three equations. If the kinetic energy is conserved and this property is invariant then the momentum is also conserved. (Note that the methodological considerations on this topics have been developed by Sorokin (1956) and reproduced by Iserman (1974).) The distinguishing feature of our model is that the Galilean transformations are not postulated but derived.
At first let us consider a simple example of an inertial frame of reference. Assume that the velocity of the center of mass of all particles is constant, i.e. ![]() where
where  . It is of interest that Mach (1904) has defined the mentioned reference frame as inertial. It can be seen from Eq. 6 that every reference frame which moves with constant velocity relative to that mentioned is also inertial. One can conclude from Eq. 8 that the total kinetic energy of all particles is constant for this class of reference frames. On the basis of the group properties one can deduce from this fact the conservation of the total momentum (however this conclusion is followed by that the velocity of the center of mass is constant). Let us propose that our system of M particles is closed (isolated), i.e. interactions of this particle system with the other particles are negligible. If we have two separated parts of the world then one can suppose that
. It is of interest that Mach (1904) has defined the mentioned reference frame as inertial. It can be seen from Eq. 6 that every reference frame which moves with constant velocity relative to that mentioned is also inertial. One can conclude from Eq. 8 that the total kinetic energy of all particles is constant for this class of reference frames. On the basis of the group properties one can deduce from this fact the conservation of the total momentum (however this conclusion is followed by that the velocity of the center of mass is constant). Let us propose that our system of M particles is closed (isolated), i.e. interactions of this particle system with the other particles are negligible. If we have two separated parts of the world then one can suppose that ![]() , where
, where 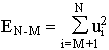 , and from Eq. 8 we deduce that
, and from Eq. 8 we deduce that  too. Because the last equality is invariant under Galilean transformations (it is valid for the mentioned class of reference frames) one can write
too. Because the last equality is invariant under Galilean transformations (it is valid for the mentioned class of reference frames) one can write
 (9)
(9)
where the infinitesimal transformations of the given group have the form (e.g. for the velocity component u0x):
 .
.
After substituting these operators into Eq .9 we obtain
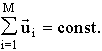 (10)
(10)
Let us multiply both parts of Eq.10 by me (we emphasize that for the simplest model of identical particles (atoms) the magnitude of the mass does not play the role, e.g. one can assume that it is equal to the mass of a nucleon). We have
![]()
 . (11)
. (11)
That is the total momentum of the system of M particles is conserved. In general let us formulate the following condition (criterion) of inertiality of the reference frame under consideration:
a) ![]() .
.
As is easy to see from the condition a) that Eq. 10 and Eq. 11 are deduced.
Note that in this general case the first sum in Eq. 8 (the kinetic energy of the system) need not always be conserved. And the following relation is not always valid

because the equality
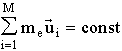
is not always valid.
Indeed, from Eq. 8 one can see that the subtraction of the kinetic energy of the world and that of the center of mass is constant. So if the total kinetic energy
![]()
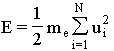
is varied then the total momentum of N particles is also varied. Assume that the infinitesimal operator Xa at M=N acted on the appropriate value in Eq. 8, then we deduce
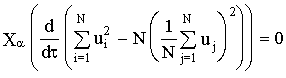 .
.
That is we have the identity

or in the vector form
![]() -
-
![]() = 0.
= 0.
One cannot conclude the identity about the conservation of the value![]() . Hence, the total kinetic energy may be constant or not. If M=1 then we have the analog of the first Newton's law. Assuming that M=2, we obtain from Eq. 11
. Hence, the total kinetic energy may be constant or not. If M=1 then we have the analog of the first Newton's law. Assuming that M=2, we obtain from Eq. 11
![]() . (12)
. (12)
Let us denote the expression on the right-hand side of Eq. 12 as the force ![]() 1,2 acted on the first particle from the second one (in such a way a concept of force is defined). Then we obtain the analog of the second Newton's law. Accordingly the force
1,2 acted on the first particle from the second one (in such a way a concept of force is defined). Then we obtain the analog of the second Newton's law. Accordingly the force ![]() 2,1 acts from the first particle to the second one and we obtain the analog of third Newton's law. If the condition a) is not obeyed then the frame of reference is noninertial.
2,1 acts from the first particle to the second one and we obtain the analog of third Newton's law. If the condition a) is not obeyed then the frame of reference is noninertial.
In the proposed model the inertial properties are consistent with the Mach principle. If the condition is not obeyed then the model describes at least all noninertial reference frames moved translationally and accelerately relative to an inertial reference frame. Let us consider, for instance, such noninertial frame of reference. Assume that its velocity with respect to the noninertial one is ![]() 0(t). We know that
0(t). We know that ![]() .
.
Assume that M=1. In the inertial frame of reference this particle (the first) moves with a constant velocity, i.e. ![]() 1=const.
1=const.
The transformations in Eq. 7 are valid, and for the translationary accelerated reference frame we obtain
![]() .
.
Of course the first Newton's law is not true here.
Let us write the form correspondent to the inertial force in this case. If we differentiate all terms in the equality
 ,
,
we obtain
 .
.
One can treat the value on the right-hand side as the force acted on the first particle from all particles of the world.
Here the Mach principle is formulated in terms of the equations of motion. However the expression for force dependent on distance needs to be introduced. For this purpose the model of rods (and space) must be constructed.
4. Effects due to the statistical character of the model and correspondence to the traditional theory
We must define the relation between the given mathematical model of clocks (the time t) and the real physical clocks (the time tc). Let us consider N vector stochastic processes. Assume that they simulate the quantities d![]() i (i=1, ..., N) (taking into account the character of obtaining "pictures"). Then
i (i=1, ..., N) (taking into account the character of obtaining "pictures"). Then  are probable functions as well. Assume for "ideal physical clock" that the following relation is valid
are probable functions as well. Assume for "ideal physical clock" that the following relation is valid
d
tc2=M0(dt2), (13)where M0 is the mathematical expectation of the probable quantity dt2 therefore, more closely
![]()
 .
.
d
tc is defined below. One can suppose that a pace of real clocks has been formed by creating more and more accurate standards of time. The value h
i averaged in such a way could correspond to the value M0(h
i) (and for all particles to the value ![]() respectively).
respectively).
Assume that independent random variables h i have finite variances and have the same distribution. Then at the conditions of the limit theorem
 ,
,
where the variance  . If this value is the order of dt2 then
. If this value is the order of dt2 then
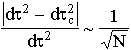 . (14)
. (14)
Of course the readings of the certain real physical clock can differ from the "ideal physical clock's readings" closed to dt according to Eq. 14 (in the framework of the adopted probabilistic model). It denotes that with a certain type of a clock (e.g. atomic) one can obtain deviations in any case not less than O![]() .
.
When N® ¥ the value dtc tends to dt (on possibility). Then, all equations of the classical theory are obeyed exactly. This is the statement of correspondence between the model and traditional equations.
It is of importance to emphasize that our equations (the value dt appears there) are, in fact, the consequences of the mathematical postulates. On the basis of mathematical axioms one can carry out from Eq. 1 some expressions (the time is measured accordingly with Eq. 1 through space variables and the original equation is, in fact, the identity). This reduction of equations to dimensionless form leads us to propose that the basis of our knowledge is the mathematical postulates and the physical sense appeared after exchanging the formal mathematical quantities into the physically measured quantities. One can say that through clocks and rods the mathematical equations are "projected" into the sensitive experience.
Therefore the mathematical value dt must be replaced by the physically measured value dtc . After this substitution the analogs of Newton's equations are valid with accuracy O![]() . Hence, those are the effects in which the developed theory is different from the traditional one. These deviations however are beyond the limits of recent apparatus: for N~1080,
. Hence, those are the effects in which the developed theory is different from the traditional one. These deviations however are beyond the limits of recent apparatus: for N~1080, ![]() ~ 10-40 .
~ 10-40 .
These deviations could be compared with the hypothesis of Lawrence and Szamosi (1974) about the mass distribution of elementary particles for obtaining the relations between fundamental quantities (so-called cosmological coincidences). These fluctuations is of the order of ![]() .
.
Note that in the project of "the fundamental theory" (Eddington,1949) all distances are determined with relative accuracies not more than O![]() hence and in this theory the fluctuations of such orders appear.
hence and in this theory the fluctuations of such orders appear.
5. Relativistic generalization of the model
Up to now the model has been restricted by the supposition that the existence of the uniform light signal gave the identical "pictures" in spaced-differed points. Let us consider more general situation where this condition will not be valid. The relationships of the special theory of relativity will be found.
At these conditions, for instance, the equality for the second "experiments" used for deducing Eq. 4 is not valid now, one can write
![]()
and correspondent d![]() i(O) =
i(O) = ![]() (2)i(O) -
(2)i(O) - ![]() (1)i(O) could not be changed by the expression d
(1)i(O) could not be changed by the expression d![]() i(AO) =
i(AO) = ![]() (2)i(A) -
(2)i(A) - ![]() (1)i(O).
(1)i(O).
Now there is no uniform (absolute) time, because dt(O) is not equal to dt'(O'). However one can try to construct the model of the proper time (in the way of mentioned words of Pauli (1956)).
The proper time in the "primed" reference frame has the form
 . (15)
. (15)
On the basis of the "proper" values measured by "the camera" connected with the particle under study (located at the origin of "primed" reference frame) the values d![]() i(OA) are defined in such a way
i(OA) are defined in such a way
d
These values are referred to the points O and A because at least for the point A the value d![]() (OA) can be determined by two "pictures" correspondent to the first "experiment" in the point O and the second "experiment" in the point A (really, d
(OA) can be determined by two "pictures" correspondent to the first "experiment" in the point O and the second "experiment" in the point A (really, d![]() '(O') = 0). Another values d
'(O') = 0). Another values d![]() 'i(OA) defined by Eq. 15 cannot be measured through the "difference" between two "experiments" at A and O. Actually: the photography images of moving and unmoving objects are different (the literature on this question is quite voluminous, see for
'i(OA) defined by Eq. 15 cannot be measured through the "difference" between two "experiments" at A and O. Actually: the photography images of moving and unmoving objects are different (the literature on this question is quite voluminous, see for
example the recent review (Bolotovsky, 1990)). Therefore the relationships between the particle coordinates for "experiments" obtained in different reference frames are not the simple shift according to Eq. 16.
Let us construct the model time interval on the basis of values
 . (17)
. (17)
As a consequence of Eq. 16
d
t(OA) = dt'(O') . (18)Now the relativistic time dt(OA) between two events (the first one is moving the point O' near to O and the second one is moving of the point O' near to A) is defined as follows
 . (19)
. (19)
Here the term which describes the "slowing-down" is added (for every term of this statistical sum). Uncover the squares on the right-hand side of Eq. 19 after summation we have
dt
2(OA) = dt2(OA)+a2dOr rewriting Eq. 20 we obtain known expression from special theory of relativity:
d
t'2(O')=dt2(OA)=dt2(OA) -a2dOne can find the limitation of the particle velocity from Eq. 20 (it is proposed that the origin O' is connectd with the particle under consideration):
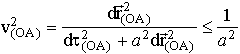 . (22)
. (22)
The quantity 1/a limits the velocity and therefore it is associated with the light velocity in vacuum, i.e.
a
= 1/c . The limiting value 1/a is attained at dt(OA)=0 or when the velocity ![]() (OA) tends to infinity. Note that from Eq. 3 it is evident that a = 1/c is the mean square velocity of particles of the world. Of course it does not contradict the theory of relativity. Indeed, the time from Eq. 15 is determined through the "experiments" in the same space point. The time interval dt(OA) is determined by the measurements in two different points. (Synchronization of such relativistic clocks is analogous to Einstein's synchronization according to Eq. 20).
(OA) tends to infinity. Note that from Eq. 3 it is evident that a = 1/c is the mean square velocity of particles of the world. Of course it does not contradict the theory of relativity. Indeed, the time from Eq. 15 is determined through the "experiments" in the same space point. The time interval dt(OA) is determined by the measurements in two different points. (Synchronization of such relativistic clocks is analogous to Einstein's synchronization according to Eq. 20).
The relation between ![]() (OA) and
(OA) and ![]() (OA) is similar to the relation between the relativistic and the proper velocities:
(OA) is similar to the relation between the relativistic and the proper velocities:
 .
.
Note that the time from Eq. 19 tends to the model time given by Eq. 1 if A tends to O (i.e. if the particle connected with the origin is unmoved). Analogously dt'(O')=dt'(O'). From Eq. 21 we have
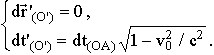 . (23)
. (23)
This is the special case of the Lorentz transformations. We emphasize that in contrast to the mentioned Galilean transformations which are valid for every point, the Lorentz transformations are valid only for one space point in which the particle under consideration is placed.
With Eq. 23 one can derive the equations of relativistic dynamics, but at first let us consider the Lorentz transformations in general. Assume as before that the first event is the moving of the particle near the origin O and the second one is the moving of it near the point B. Now the point B' (not consistent with O') is correspondent to B. As before the point A' is correspondent to O'. Let us associate a given particle with the origin O'' of the proper reference frame. The proper time at this point is written analogously as Eq. 15:
 . (24)
. (24)
By means of the quantities d![]() "i(O") obtained through two "experiments" in the given reference frame the quantities d
"i(O") obtained through two "experiments" in the given reference frame the quantities d![]() 'i(O'B') and d
'i(O'B') and d![]() i(OB) for "primed" and "laboratory" reference frames respectively are defined analogously as Eq. 16.
i(OB) for "primed" and "laboratory" reference frames respectively are defined analogously as Eq. 16.
d
Let us introduce the following quantities:

One can see from Eq. 25 that these values are equivalent to the value of the time interval Eq. 24:
dt '
(O'B')=dt "(O"), dt (OB)=dt "(O").Define the relativistic time analogously to Eq. 19
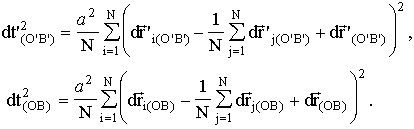
And one can find the final relation
![]()
It follows hereof the Lorentz transformation in general situation (if it is supposed as usual the linear dependence between dt'(O'B') and dx'(O'B') on dt(OB) and dx(OB)).
The equations of dynamics with the invariant time are deduced in the same manner as in Eq. 3. Because the form of this statistical function of time in Eq. 17 is the same as in Eq. 1 the equation of motion will be similar. For example for a certain particle (first) one can write
![]() . (26)
. (26)
Here the invariant form of the relativistic dynamics equation is presented. The three-dimensional part of the four-vector of the Minkowski force appears in the right-hand side of Eq. 26. Changing dt to dt we have
 ,
,
where  is the relativistic momentum of particle,
is the relativistic momentum of particle, ![]() is the relativistic generalization of Newton’s force.
is the relativistic generalization of Newton’s force.
Introducing the work in the usual manner we obtain from Eq. 26 the known expression for the relativistic energy.
If the number of particles N is finite, there is a distinction from the standard theory. Strictly speaking the conclusion about the limitation of mass of the metagalaxy could be made only after developing the model for general relativity case (it is required to construct the model of rods). However, statistical effects of mentioned order must, in our opinion, appear at several levels of the theory (in particular as small fluctuations of metric). On the other hand the magnitude of the square root of N corresponds to the so-called cosmological coincidences. It is interesting to note that H.Weyl (1949) said that the Mach postulate is awaiting the theory itself (would be the statistical theory of gravitation, to which the square root in the law e![]() points to)?. Here the hypothetical relation between e (the ratio of the constants of gravitational and electromagnetic fields) and the number of particles N is discussed.
points to)?. Here the hypothetical relation between e (the ratio of the constants of gravitational and electromagnetic fields) and the number of particles N is discussed.
6. Properties of time and possible improvements of the model
Up to now mainly the metric time properties of the clock model were studied. However, one can note that the given model has a "surplusity" allowed to describe time features in more detailed way as compared with the traditional model. Namely in our constructions the notion "time instant" is the state of the world characterized by 3N parameters in the configuration space.
Here the numerous philosophical problems connected with the concept of time are not discussed. Note that only the given model time is associated with the concept "motion". The ontological basis of the given time is in the original possibility of distinguishing "subject" - "object". The question about origin of motion in the world is not considered now.
Let us describe briefly the peculiarities of fixing of particles motion itself in the model. So we consider the elements from which the time interval has been constructed. The problem of "the present" has been discussed in detail by Aristotle. In the given model "the present" (i.e. "instant") is purely spatial, it has no temporal characteristic. The time is added by small intervals which are determined through differences of "instants". As mentioned above the pairs of "pictures" have been used for this process. Note, however, that in the "pictures" not only the radius vectors ![]() i are fixed but the small values d
i are fixed but the small values d![]() i too. Indeed, "the camera" has a finite time of photographing, therefore all moving particles images are "unclear". Hence, the traces of particle motions are given. The origins and the ends of the vectors d
i too. Indeed, "the camera" has a finite time of photographing, therefore all moving particles images are "unclear". Hence, the traces of particle motions are given. The origins and the ends of the vectors d![]() i can be fixed. For example when one pushes the camera button the red light filter could be worked and at the end of the photography process the blue light filter could be worked. Thus the origins of mentioned vectors are red and the ends of the vectors are blue.
i can be fixed. For example when one pushes the camera button the red light filter could be worked and at the end of the photography process the blue light filter could be worked. Thus the origins of mentioned vectors are red and the ends of the vectors are blue.
1) Description of time course and the problem of "reversible time"
In the definition of dt in Eq. 1 the question about the time direction has not been set yet. Here the quadratic quantities appear. It shows that the sequence of "experiments" is not of importance. The sign of dt is chosen as positive. It is correspondent to the fact that the classical time has one direction. And as a result the equations of mechanics with reversible time have been obtained. (Traditionally the reversibility of time in mechanics is understood as a fact that the equations are invariant relative to the alternation of signs of time and particle velocities.)
However the question on the reversible time can be set in a wider sense than in mechanics itself. Let us consider the description of time course. For this aim one have to use more complex instrument, namely "a camera with a memory", i.e. "the camera" supplemented by the apparatus capable to fix the order of obtaining "experiments". (Note that some philosophers suppose that the concept of memory is necessary to define the idea of time).
At first "the memory" in such apparatus is blank. Let us obtain "the experiment" and memorize it. Note this "experiment" by the number 1. Obtain the other "experiment" for which all radius vectors are different from the first one at the infinitesimal magnitudes. For the new "experiment"which is also fixed in "the memory" number 2 is assigned and so on.
It is of importance that here there is no originally given sequence of time instants. The mentioned procedure of construction of instants is sufficient for modelling the intuitive understanding course of time. One can connect the sequence of "experiments" obtained by such manner with the increasing set of integers. (This process is analogous to some extent to the changing of integers in an electronic clock.) This sequence determines the direction of time.
"The irreversibility" of time is connected with the differences of "experiments" at the different moments of time. The possibility of a coincidence of two different "experiments" is extremely small if particle movements are random. If a certain "experiment" is identical with the other "experiment" then could be assumed that the time "passed back" (from the dynamical point of view two states of the world will be identical if not only the radius vectors but also all particles' velocities are the same). This situation of a negligible possibility is assoiciated with "the reversibility" of time.
2) Generalization of the model time for different particle systems.
The model clocks (and accordingly the times) could be constructed for different numbers of particles in the system under consideration. The minimum particle number is 2. If there is only one particle then the model time does not pass because the frame of reference must be connected with this particle.
"The internal time" of a system of N1 particles could be introduced by the sum analogously to Eq. 1. If this number is small, then one can control the time course of such "microcosm". The multiplier a2 in Eq. 1 describes the thermodynamical properties of the world. For the system with N1 the other multiplier a12 can be used. It characterizes the thermodynamical properties of this system itself and is equal to the ratio of the particle mass and the system temperature. Therefore one can construct the hierarchy of "the inner times" for systems with different numbers of particles: N1, N2,... . "The world time" with the limiting large number N is the limiting scale in such hierarchy.
May be it is more convenient to use the single multiplier a2 for comparing the different "inner times".
One can try to extrapolate these notions of the physical time to more complex systems where the biological, the geographic, the geological times could be defined. Some quasiparticles must be determined in the given systems. Then "the inner time" could be constructed by the mentioned manner through observing the moving of such "particles".
It is of interest to generalize the model for nonequilibrium systems itself. It is desirable to construct "the nonequilibrium time", i.e the time which does not run when the system is at equilibrium. At the enthropy maximum of the closed system such time will be stopped (it corresponds to some scientists' way of thinking that the time concept must be introduced for nonequilibrium systems only). Emphasize that in this situation the time interval from Eq. 1 is not equal to zero.
This is not the homogeneity in the nonequilibrium system, therefore for generalization let us divide the system into p parts. Every part is at near homogeneous conditions. Assume N is the number of particles in the system, then
 .
.
For every part "the inner time" is constructed. Let us define the interval of "the nonequilibrium time" as
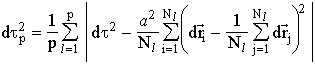 ,
,
where dt2 is introduced for the system of N particles through Eq. 1. The sense of such "nonequilibrium" time interval is the following. Here the mean deviation of the motion characteristic of every part from the analogous total value appears. At nonequilibrium conditions ![]() >0. At equilibrium when separated parts are approximately homogeneous
>0. At equilibrium when separated parts are approximately homogeneous ![]() = 0. I.e. the value
= 0. I.e. the value ![]() is related qualitatively with the Boltzmann
is related qualitatively with the Boltzmann ![]() . It seems that the searching relationships which are more complex than Eq. 1 is important. Thoughts about "irreversible time" from 1) could be used and could be referred to hypothetical "irreversible in time" equation (as e.g. the kinetic Boltzmann equation).
. It seems that the searching relationships which are more complex than Eq. 1 is important. Thoughts about "irreversible time" from 1) could be used and could be referred to hypothetical "irreversible in time" equation (as e.g. the kinetic Boltzmann equation).
3) On modeling of time equability (time congruence)
Based on intuitive considerations, Eq. 1 is capable to model the time equability. Let us define more exactly why the averaging over the particles gives the possibility to describe equable course of time.
The concept equability itself needs clarification. Reihenbach (1958) noted that, as for spatial variables, for time it must used the idea of the so-called coordinate definition. The question of comparison of two time intervals is the problem of a convention. One of the possible independent definitions of time equability (time congruence) by Reihenbach is given by mechanics laws. In this sense our time model satisfies the demand of such convention.
The next definition of equability is given using clocks which can be dealt with the problem of equability of ordinary clocks. As was mentioned above, it seems, that clock's pace has been improved over the course of long historical time, particular in the sense of reaching greater equability. Time units defined by motion of the moon, the sun and other objects have been corrected permanently. The pace of real clocks has been established by creating more precise (in certain sense) standards of time units. Working out of standard clocks' pace has been taking place a long time by using some averaging in fact by "experiments". It may be said that clocks' pace little by little has been arranged on a pace of all world objects (by comparing "temporal" scales of systems and particles).
In the framework of present model these notions could be illustrated by the following simple example. Let N particles in a system move independently, but realize the same probable value. The realization of the probable value for "i" particle is d![]() i , and in accordance with the mentioned notation
i , and in accordance with the mentioned notation 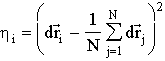 . The mean over realizations tends to the expectation under the increasing of the number of realizations:
. The mean over realizations tends to the expectation under the increasing of the number of realizations:
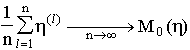 .
.
Here n denotes the number of probable trials. (Any probable value hi denoted as h is considered.) In a given simplest example averaging over N probable values hi can be considered as averaging over a large number of realizations of the single probable value. If it is possible to construct an instrument (a clock) which can be arranged on the average pace of particles (in a given example on the average motion over realizations of the single particle) then one can obtain the equable time course, i.e. always reproduce the value M0(h ). And one can model this averaging (over the large time interval) value by Eq. 1 at a fixed moment of time. Indeed, with the notations of Section 4 we have
 .
.
This equality is obeyed with accuracy O(![]() ).
).
Such considerations have a shortcoming because all operations have been made with unnormalized values hi the normalization denotes that we deal with appropriate velocities; for these probable values one must write analogous expressions.
4) Properties of the model time
In conclusion let us consider some general properties of the time described on the basis of proposed model of clock. This time is relational, dynamical, conventional and universal. However, one can construct "internal time" for every system with the number of particles less than the limiting one. The time is uninterrupted because thus far coordinates of all particles are described in the classical manner, i.e. on the basis of continual space. Since the time is determined through Eq. 1 it is one-dimensional. However more detailed measures are acceptable. One can say that the model time as the characteristic of all changes in the world is determined by all 3N coordinates, in other words, that time is 3N-dimensional.
Let us note briefly the possibilities of developing the model. One can propose other mathematical forms of the time interval, in which, for instance, values of radius vectors differentials would be with weights dependent on distances between "the camera" and particles. For arrangement of physical sense into such construction it needs to create a new clock capable of taking the average motion of particles in accordance with the formula for the time interval. Then the form of dynamics equations will be changed. Thus the problem of generalization of the model could be realized by constructing new instruments. More detailed description of reality would be achieved through obtaining the new temporal characteristics of motion.
REFERENCES
BOLOTOVSKY B.M. (1990). On visual form of moving body. In: "Einsteinovskii Sbornic" (Einsten's transactions). 1986-1990. Pp.279-328 (in Russian).
EDDINGTON A. (1949). Fundamental Theory. Cambridge.
EINSTEIN A. (1949). Autobiographical notes. In: Albert Einstein: Philosopher-Scientist. N.Y. Pp.60-61.
ISERMAN A.I. (1974). Classical Mechanics. Moscow. Pp.46-47 (in Russian).
LAWRENCE J.K. and SZAMOSI G. (1974). Statistical physics, particle masses and the cosmological coincidences. Nature. V.252. Pp.538-539.
MACH E. (1904). Die Mechanic in ihrer Entwickelung Historisch - kritisch Dargestellt. F.A.Brockhaus. Leipzig.
PAULI W. (1956). Schlubwort durch den Prasidenten der Konferenz. In: "Funfzig Jahre Relativitatstheorie". Helv. Phys. Acta. 1956. Suppl.4. S.263.
POINCARÉ A. (1913). Derniйres pensйes. Paris.
REIHENBACH H. (1958). Philosophy of Space and Time. N.Y.
SOROKIN V.S. (1956). Conservation laws and a measure of motion in physics. Uspehi fisicheskih nauk (Advances of Physical Sciences). V.IX. N.2. Pp.325-362 (in Russian).
WEYL H. The main features of the physical evolution; morphe and evolution. in: Philosophy of mathematics and natural science, Appendix.F.Princeton. Pp.285-301.
ZIMMERMAN E.J. (1962). The macroscopic nature of space-time. American Journ. of Physics. V.30. N.2. Pp.97-105.