A. P. Levich

N.A.Kozyrev, an outstanding astronomer and natural scientist, enriched the dynamic picture of the World by introducing a new entity, possessing “active properties” and coinciding with neither matter, nor field, nor space-time in its usual understanding.

This entity is difficult not only for intuitive or logical perception but also for a verbal description since a proper complex of concepts and images for dealing with the new ideas is yet to be developed. The researchers “read” N.A.Kozyrev’s works in different ways, accentuating different aspects and viewing the subject from different angles. Thus naturally non-coinciding interpretations of N.A.Kozyrev’s ideas come into existence. I.A.Yeganova exposes N.A.Kozyrev’s views by introducing a “meta-interaction, embracing the whole material world and mediating the existence of all the manifestations of matter by self-regulation in a unified universal process” (Yeganova 1984, p.2). Therewith it cannot be excluded that “there exists a material carrier (a certain medium), directly “converting” cause into effect” (Yeganova 1984, p.32). S.M.Korotayev (see his chapter in this volume) stresses in N.A.Kozyrev’s time conception the causal nature of the fundamental irreversibility, also recognising that N.A.Kozyrev’s causal mechanics contains a substantial time construction.

In the present review it is suggested to look at N.A.Kozyrev’s ideas basically from the standpoint of their substantial interpretation.

N.A.Kozyrev imagined time as “a mighty flow embracing all the material processes in the universe, and all the processes taking place in these systems are sources feeding that flow” (Kozyrev 1963, p.96). The author writes about the intensity or density of the time flow, the energy it carries, its emission and absorption, the rectilinearity of its propagation, its reflection from obstacles and absorption by matter... By N.A.Kozyrev, “time flows into a system through a cause to an effect” (Kozyrev 1971, p.118). “There is an impression that time is pulled inside by a cause and gets denser at the location of an effect” (Kozyrev 1971, p.129). “... In every process of Nature time can be formed or spent” (Kozyrev 1971, p.129). Therefore it appears to be reasonable to identify N.A.Kozyrev’s flow with some substantial flow whose source is, by Kozyrev, any irreversible, out-of-equilibrium process (he apparently meant the processes accompanied by system energy and thermodynamic entropy changes). The arguments which had convinced N.A.Kozyrev that the conception of time flow was necessary, can be estimated to be speculative; however, most of his views resulted from many years of experiments. The experimental material is discussed in detail in the subsequent sections of the review.

Kozyrev pointed out the sharp contradiction between the second law of thermodynamics which brings nearer the thermal death of the Universe, and the absence of any signs of equilibrium in the observed diversity of the Universe. He stressed that “the attempts to explain the absence of thermal death have been quite apart from the real Universe observed by the astronomers. The point is that the celestial bodies and their systems are so well isolated from each other that their thermal death must have occurred much sooner than any external system could interfere. Therefore degraded states of systems ought to dominate, whereas they are almost never met. And the task is not only to explain the non-equilibrium state of the whole Universe, but also to gain an understanding why separate systems and celestial bodies themselves continue to live despite the short relaxation times” (Kozyrev 1963, p.96).

Various hypotheses are possible attempting to “save” the second law of thermodynamics. For instance, the one asserting that the Universe is isolated indeed but the present moment of cosmological time is not very far from the “initial” fluctuation (singularity, cataclysm), so that the signs of degradation cannot be too clear, i.e., the “death” is postponed to a remote future. N.A.Kozyrev suggested an alternative version: the Universe and its subsystems are not isolated, i.e., the necessary condition for the second law of thermodynamics is not valid: “there are permanently acting causes in nature, preventing entropy increase” (Kozyrev 1958, p.3). A necessary factor, violating the isolated state of systems, is just the Kozyrev flow.

“The problem of surmounting a thermal death of the World is most closely connected with that of the origin of solar and stellar radiation” (Kozyrev 1958, p.4). “It is of interest that even such a concrete question, namely, why do the Sun and the stars shine, i.e., why are they out of thermal equilibrium with the ambient space, cannot be answered within the known physical laws. This conclusion follows from astronomical data analysis. The radii, masses and luminosities, i.e., energy release per unit time, are known for many stars. From known mass and radius one can estimate not only mean density but also pressure inside the star. For a perfect gas the ratio of these two quantities determines the temperature inside the star. A comparison of temperatures and densities obtained in this way shows that the matter inside stars, except white dwarfs, is indeed a perfect gas. A star’s luminosity should depend on its size and heat transfer conditions, determined ultimately by the temperature and density. Therefore stellar luminosity should be a certain function of stellar mass and radius. In a space parametrized by luminosity, mass and radius the stars should align themselves at a certain surface whose equation is to be determined from heat transfer conditions. Now assume that inside a star certain heat generation processes, depending on physical conditions and compensating the heat transfer, take place, for instance, thermonuclear reactions. Then heat generation will be equal to luminosity and depend on the star’s mass and radius according to the law characteristic of that reaction. Thus in the “luminosity-mass-radius” space another surface emerges where the stars should be located. Provided the thermal equilibrium condition is valid, stars can exist only at the line of intersection of the two surfaces, that of heat transfer and that of heat generation. What is actually the case, the stars are situated at a certain surface rather than a line, occupying a significant domain. This indicates that no specific energy source exists inside the stars. In these conditions stellar lifetimes, as calculated by Helmholtz and Kelvin, are too short: e.g., only about thirty million years for the Sun. Actually, by reliable geological data, the Sun lives much longer than that” (Kozyrev 1963, p.96).

I.A.Yeganova (1984a, pp.4-5) commented: “Unfortunately N.A.Kozyrev’s works, above all analysing in detail the question of whether there are necessary physical conditions in stars for the corresponding thermonuclear reactions, were not apprehended and therefore could not affect the further development of ideas in this field: at that time everybody was “bewitched” by G.Bethe’s thermonuclear cycles (Bethe 1968). The thermonuclear stellar energy paradigm got its first appreciable stroke from the first Brookhaven experiments performed by R.Davis and aimed at discovering solar neutrino, indicators of the thermonuclear nature of solar energy. The researchers had to admit that “we understand worse than we used to believe even the structure of main-sequence stars” (Sciama 1973, p.16), that “other energy sources can also exist in stars” (Sobolev 1975, p.479). There appeared other suggestions concerning stellar energy sources, see, e.g., papers cited in the article by E.S.Meksi (1982). Other significant discrepancies in stellar structure and evolution theory resting on thermonuclear reactions, became known. They are connected with many modern data of geology and paleoclimatology and also with the discovered 160-minute oscillations of the Sun (Severny 1983). However, the most recent results obtained by Davis’ group, although indicating the solar electronic neutrino flux 3 or 4 times smaller than that predicted by theory, ... did not encourage the physicists to perform the necessary revision of the idea of thermonuclear origin of solar energy (Kopysov 1983; Davis 1983; Pontecorvo 1983). In such a situation N.A.Kozyrev’s works (1948, 1951) preserve their significance as those revealing the inherent inconsistency” of the above ideas. Recall that, according to Kozyrev, “stars are machines” getting energy from the “time flow”.

Kozyrev’s flow manifests itself in many mechanical phenomena. Irreversible processes rotate the beam or disk of a torsion balance when they, in the experimenters’ viewpoint, emit or absorb Kozyrev’s flow. (For instance, in Kozyrev’s experiments those processes included body deformations, encounter of an air jet with an obstacle, sandglass operation, light absorption, friction, burning, some observer’s actions, body heating and cooling, phase transitions in substances, their dissolving and mixing, plant fading and non-light radiation from astronomical objects.) It turns out that the flow can be absorbed, shielded or sometimes reflected by bodies. Inelastic processes in rigid bodies change their weight, while elastic bodies change their elasticity characteristics. Whipping tops change their weight when involved in an additional process, such as vibration, heating or cooling or electric current transition. Many features of the Earth’s figure and climate, as well as those of other planets, are explained by their being gigantic gyroscopes subject to the influence of dissipative processes.

The flow, accompanying dissipative processes, causes also responses of non-mechanical detectors such as resistors’ resistance values, mercury level in thermometers, quartz crystal vibration frequencies, thermocouple electric potentials, water viscosity, electronic work function in photoelectric cells, chemical reaction rates, bacteria and plant growth parameters. The effect magnitudes depend on the energy characteristic of the initiating processes, on geographic latitude of the experiment site (for mechanical experiments), on season, on additional active non-equilibrium processes occurring in the neighbourhood of the detectors, and on some other irregular and sometimes unclear conditions of the experiment. In I.A.Yeganova’s opinion (Yeganova 1984, p.10), numerous phenomena observed apart from N.A.Kozyrev exhibit the influence of background non-equilibrium processes on detectors, similar to those observed by Kozyrev: “...the so-called kinetobaric effect (Peschka 1979), J.Pichardi’s experimental results (25-year observations of the bismuth chloride precipitation rate) and those due to S.V.Tromp (observations of erythrocyte precipitation rate) (Meksi 1982), flicker noise (Zhvirblis 1983; Gertsenshtein 1983), the observation of torsion balance oscillation period increase during the 1970 total solar eclipse (Saxel and Allen 1970) and the similar results of metrologists V.S.Kazachok, O.V.Khavroshkin and V.V.Tsyplakov (1977) who repeated these experiments during the 1976 solar eclipse, the results of A.Shapovalov’s (1973) three-year observations of photomultiplier dark current”, see also a discussion of some of these effects in N.A.Kozyrev’s works (1971, 1982).

We would like to add that Kozyrev’s flows may turn out to be the universal cosmophysical cause leading to correlations between macroscopic fluctuations which show itself by equally shaped histograms describing quite different processes, from biochemical reactions to radioactive decays, in simultaneous experiments separated sometimes by thousands of kilometers (Shnol et al. 1985). Moreover, the experiments carried out by Kozyrev and his colleagues were to a large extent dedicated to direct detection (and application for astronomical measurements) of non-electromagnetic flows from planets, stars, galaxies, stellar clusters and nebulae.

It should be noted that it is very hard to combine N.A.Kozyrev’s views with the existing physical outlook. The effect magnitudes in Kozyrev’s experiments are small: the additional forces in his mechanical experiments are just about 10^-4 - 10^-5 of the weight of a body under study; in a mechanical detector operation the relative change of measured quantities due to Kozyrev’s flow can be as much as 10^-6 - 10^-7 of the forces already active in the system.

Here is how N.A.Kozyrev illustrates the difficulties of discovering hidden additional stellar energy sources, connected with the local smallness of the effects: “We get to a situation like that of a physicist in a laboratory situated deep in space, far from the Earth. He would hardly come across the forces of gravity in his experiments. However, these are just the forces which determine not only the dynamics of celestial bodies but also their internal structure. The similarity is that a star is a surprisingly perfect thermos, despite the enormous energy losses. For instance, the solar substance, having the temperature of about ten million degrees, can be cooled, according to the Helmholtz-Kelvin scale, by just one degree in three years! The trifling energy inflow needed to compensate such an expenditure, could hardly attract anybody’s attention in laboratory conditions” (Kozyrev 1977, p.210). “The experimental results show that the organising property of time exerts a very small influence on systems, compared with the usual, destructive course of their development. Therefore it is not surprising that this... entity has been missed in our system of scientific knowledge. However, being small, it is distributed everywhere in nature and only the possibility of its being stored is needed” (Kozyrev 1982, p.71).

In general, the effects observed by Kozyrev could be explained by more prosaic factors than the “time flow” (for instance, by convective flows, cooling or heating effects, induced electric or magnetic fields, etc.). N.A.Kozyrev tried to analyse the possible role of alternative factors in his experiments, for instance, he dedicated a whole article to possible mechanisms causing different effects in vibrating bodies being weighed at a beam balance. However, his opponents can always find objections connected with some unstudied factors. Moreover, a reader always rightly expects that a thorough analysis of errors, which are able to turn the observed effects into vexing artefacts, is the author’s trouble. At any rate, by now neither a concrete disproof of N.A.Kozyrev’s experimental results exists, nor their consistent explanation by common physical factors. There is just a reasonable doubt concerning the unambiguity of interpretations of the experimental data.

Judging from the existing publications, by now some of N.A.Kozyrev’s experiments have been reproduced and confirmed by a group of Novosibirsk experimentalists (Lavrentyev, Yeganova et al. 1990; Lavrentyev, Gusev et al. 1990; Lavrentyev et al. 1991, 1992). Besides, G.Hayasaka and S.Tekeychi (1989) discovered certain effects, similar to Kozyrev’s, while weighing gyroscopes (probably they had no idea of the results of their Russian colleague). The work of the Japanese experimentalists caused a tough controversy in physical journals. Neither French (Quinn and Picard 1990), American (Faller et al. 1990; Nitschke and Wilmarth 1990), nor other Japanese opponents (Imanishi et al. 1991) observed the gyroscope weight lessening effects like those detected by Kozyrev, Hayasaka and Takeuchi. Kozyrev’s experiment methodology (see the details in Section 2.11 of the present chapter) required that the weighed gyro necessarily take part in some additional irreversible process like vibration, heat conduction or electric current transition. G.Hayasaka and S.Takeuchi stressed that in their experiment a mechanical vibration of the gyroscope took place and vibration damping was provided by “a pillow of foamy polyurethane laid under the gyro”. Though, in the experiments where Kozyrev’s effects were not observed, both spring suspensions (Faller et al. 1990) and polyurethane foam (Quinn and Picard 1990) have been used for vibration damping; the other two papers do not mention any irreversible process.

Apparently the intention to repeat or further develop Kozyrev’s difficult experiments is prevented by the comprehension difficulty of Kozyrev’s works, where unfortunately no attempt was made to adapt his original ideas and terms to the existing standards and traditions of the scientific establishment.

N.A.Kozyrev’s scientific views repeatedly turned out to be in sharp contradiction with his colleagues’ paradigms. That was unable to prevent him from making outstanding discoveries in astronomy, in particular, he predicted and discovered lunar volcanism. Maybe, the intuition did not deceive our extraordinary contemporary when he predicted the substantial nature of time?

“...The torsion balance version with strongly unequal arms... has turned out to be perfect. The suspension point was placed near the big weight whose mass was chosen to be about ten times as big as that of the smaller one, attached to the longer arm of the beam. This longer arm is a long flexible pointer with a loading of about 1 gram at its edge. The beam was suspended on a capron filament of 30 micrometer diameter and 5-10cm long. The whole system was placed under a glass cap able to be evacuated. A metal net surrounding the cap protected the system from possible electromagnetic influences... Any irreversible process being carried out in the neighborhood of the balance, caused a rotation of the pointer either to the process, or in the opposite direction, depending on the character of the process. For instance, cooling of a previously heated body caused pointer rotation to that body, while a body being heated deflected the pointer to the opposite side. The pointer turned out to be affected by a great variety of irreversible processes: salt dissolving, body compression or stretching, simple mixing of liquid or dry substances and even the work of a human head” (Kozyrev 1971, pp.130-131). “The observed balance rotations were as big as tens of degrees, corresponding to forces of about 10^-3-10^-4 dyne. Thus, as the beam weighed a few grams, its rotations were caused by forces of 10^-6-10^-7 of the forces acting in the system” (Kozyrev 1977, p.217).

Astronomical observation with a torsion balance “were carried out at the coude focus of the telescope. In the course of such observations the balance could be at rest at a reliable foundation. A star was projected through the glass lid of the can onto its bottom, near the longer arm of the beam, and then its light was screened by a black paper... Some celestial objects indeed caused reliable, repeatedly confirmed beam deflections. Figure 1 shows an example of a detected balance deflection in an observation of the star hCas by the telescope PM-700. The columns labeled “0” mark the time intervals when a stellar action on the balance was removed. Although the observations were accomplished in rather favourable conditions, the zero point drift of the balance due to the ambient processes was very significant. However, on the background of the drift, the star’s action is seen quite distinctly, causing balance deflection of 5°. Approximately the same effect was demonstrated by the famous X-ray source Cyg X-1.

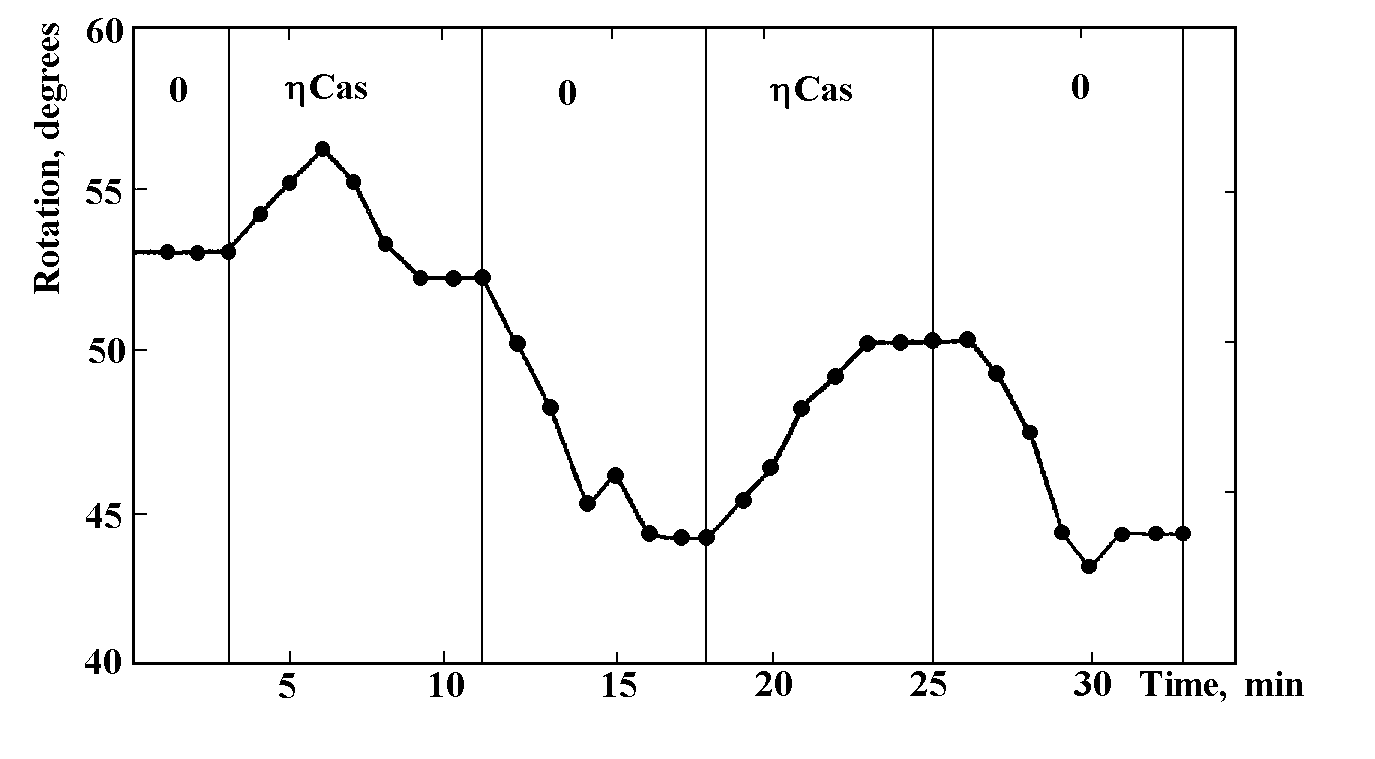
Now let us give a summary of all the astronomical observations carried out using the torsion balance. The summary includes only repeatedly observed objects.

1. Objects showing no balance deflection, Dj = 0°. Stars: aAgl, aAur, aBoo, aCyg, aHer, aOri, aTau, bCem, gCas, 61 Cyg. Cepheids: hAgl, S Sge. Pulsar CP 1133. Other objects: globular cluster M13; open clusters: Crib, x Per; Lyra and Orion nebulae; galaxies M82 and NGC 1275, the Seyfert one; the planet Saturn.
2. Small deflections, Dj: 2-3°. Galaxies: M81, Virgo cluster NGC 4594, the Andromeda nebula.
3. Significant deflections, Dj: 3-5°. aCMa, aLeo, hCas, white dwarfs: W 1346, Hert z3, z43; the source Cyg X-1 and the Galactic center.
4. A big deflection of Dj = 9° (averaged from 14 observations) was given by aCMi.
5. Variable deflections. The Moon showed extremely irregular deflections, independent of its phase, between 0 and 4°. Venus showed still bigger variations of Dj, from 0 to 12°” (Kozyrev 1977, pp.218-219).

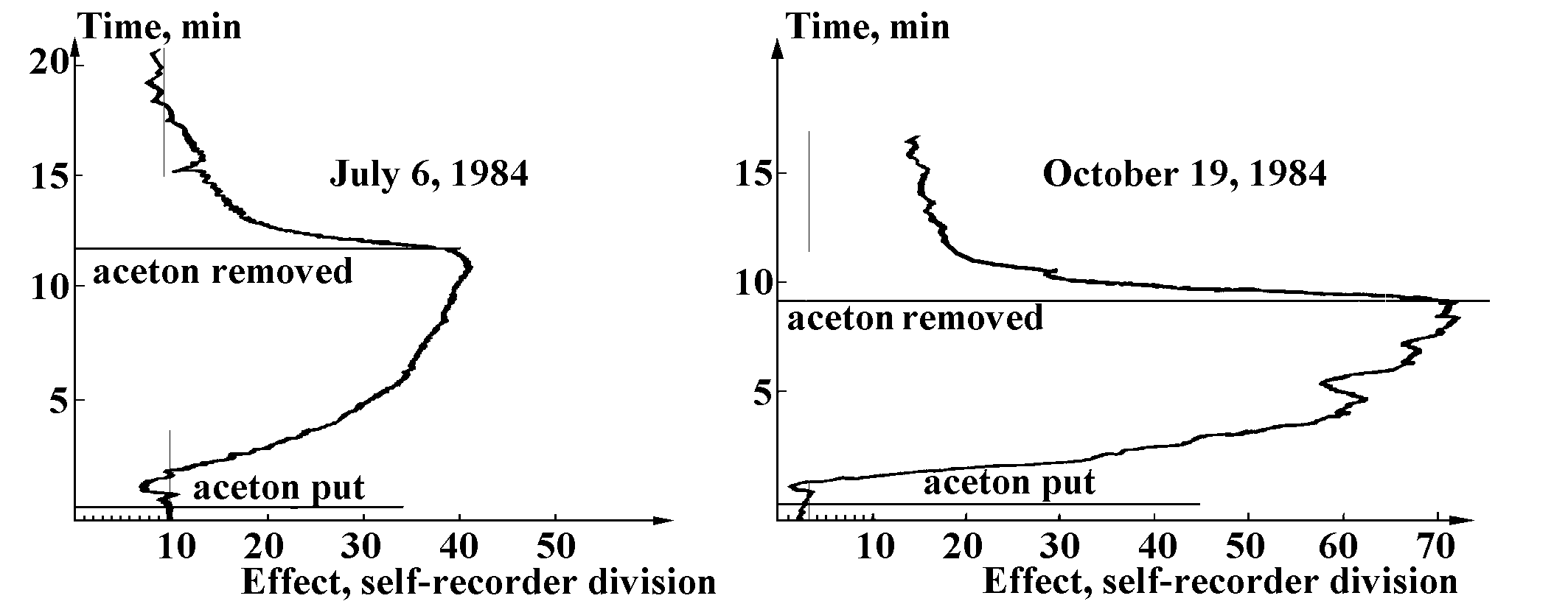
Instead of a beam with unequal arms, one could use a continual homogeneous disk, suspended by its center, in a torsion balance. “A thick shield was put on the glass lid of the can, with an opening over the disk suspension point. Due to such a protection, the process could affect only the disk suspension point. When the processes are carried out,... the disk rotates... For successful experiments disks as homogeneous as possible are needed. Therefore we employed light disks of pressed, unrolled cardboard. Even a line on the disk was inadmissible, so for fixing the rotations we used just a small mark on its edge” (Kozyrev 1977, p.220). “Acetone evaporation over the suspension point caused disk rotation of a few degrees. We have been unable to achieve a clear understanding of the action of this instrument.” (Kozyrev 1982, p.65).

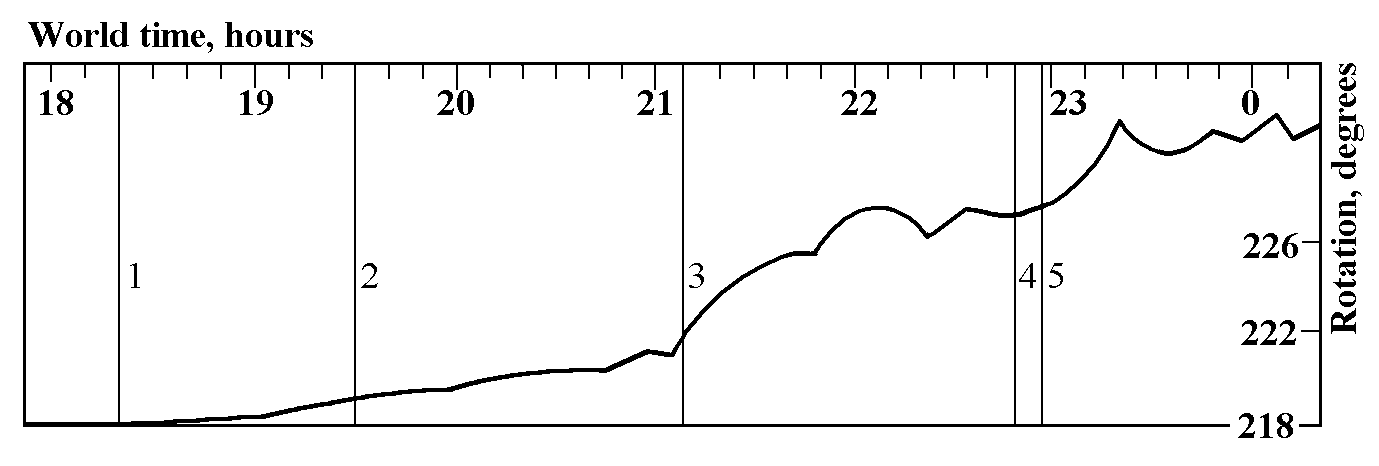
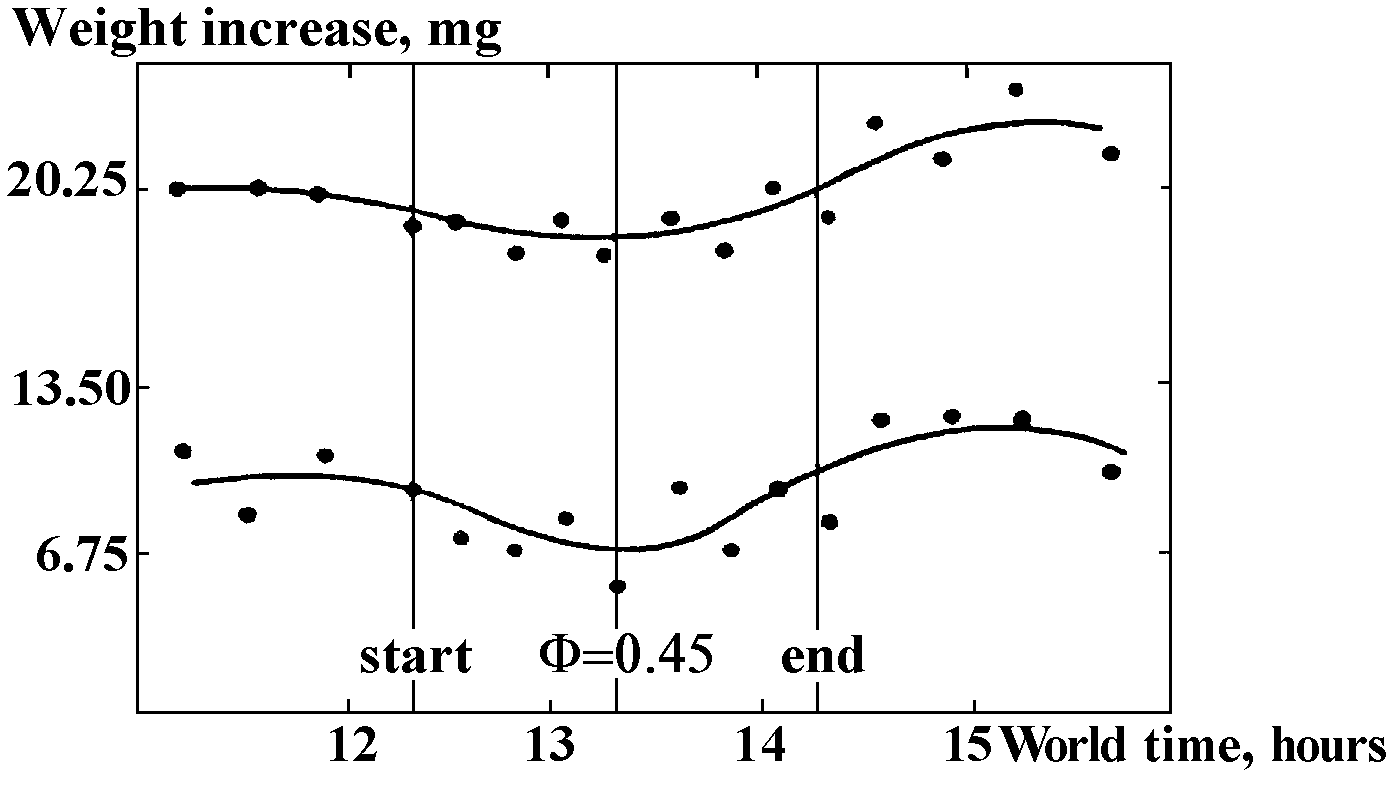
“Probably a disk is a better instrument for astronomical observations than a non-symmetric torsion balance: when working with a disk, a star is to be projected upon the unambiguously determined point of its suspension” (Kozyrev 1977, p.220). “During an eclipse the lunar surface is for a short time, about a hundred of minutes, cooled down from 100°C to -120°C and afterwards heated to the previous temperature... Such observations were carried out during the partial (but with a big phase F = 0.86) lunar eclipse on 13-14 March 1979... During the eclipse the disk was in a sufficiently stable environment of a semi-underground room. The disk positions were detected every 5-10 minutes” (Kozyrev 1982, p.65). Figure 2 “shows the position angles of a mark on the disk. The graphs show that the counts began changing indeed after the maximum eclipse phase had passed, when the parts of lunar surface, freed from the Earth’s shade, started to be heated. The second change in the disk counts was observed when the Moon was leaving the semi-shade, the normal solar irradiation being restored at the lunar surface” (Kozyrev 1982, p.65).

“The laboratory experiments with plants should be described in more detail. The experiments were carried out on non-symmetric torsion systems where pointers made of jasmine, bamboo and glass were suspended by capron filaments, and also on a torsion disk of glossy paper. The systems were confined to tin cylindrical cans with hermetically mounted glass lids for observation. Many plants growing on the campus of Pulkovo observatory and picked in different seasons (apple-tree, pear-tree, linden, chestnut, clover, dandelion and others) took part in the experiments. The experiment methodology was the following. The plants were brought to the laboratory, laid down on a table, each one separately, for a certain time, and after that laid by a top or a cut near the torsion balance at a spacing of about 30° from the pointer direction (or from a mark on the disk), at either side from it consecutively... In the overwhelming majority of the experiments the plants caused deflections of the torsion balance and the disk, but it was impossible to repeat the results. The values of these effects varied both in magnitude and in sign. The reference process, namely, acetone evaporation from a piece of cotton wool, always led to a repulsive pointer deflection and to a clockwise disk rotation... The effect magnitudes from the plants varied from season to season from 1-2° to nearly a round trip, with different effect signs... At the first instant after being picked up a plant... causes a pointer deflection away from it. The effect sign is the same for the cut and the top, while the quantitative values slightly differ. In the second period... the stem continues to repel the torsion balance pointer with nearly the same strength and intensity (always steadily and moderately), while the top begins to attract it very actively, sometimes with pulsating pushes... For instance, a blossoming apple-tree branch before petal dropping can cause an attraction effect of 250-300° for 5 to 10 minutes. The usual repelling effect of an apple-tree branch ranges from 10° to 30° and is observed for the same time... In 1983 the Pulkovo apple-trees exhibited an autumn increased activity period. It is known, however, that it is just the period when apple-trees lay the basis for the following year harvest. The following year apple harvest in Pulkovo was very rich indeed. Autumn observations of 1984 did not reveal such an activity of apple-trees, and next summer only some trees yielded an apple harvest... It is remarkable that a significant plant number increases actually... did not result in an increased effect.”

“It has been established that... common human activity only slightly changes a measurement system state... A sick person comes into active interaction with measurement systems, moreover, this interaction begins much earlier than the person notices his disease. In some cases N.A.Kozyrev and I found out that we had caught cold one or two days earlier than we felt unwell and the body temperature rose. The measurement systems are especially strongly affected by a person in emotional excitement. For instance, N.A.Kozyrev was able to deflect a torsion balance pointer by 40° or more when reading his favourite “Faust”. Meanwhile, as a rule, mathematical calculations did not cause pointer deflections.”

These quotations have been taken from V.V.Nasonov’s talk entitled “Time of physics and the life of Nature” (pp.3, 4, 15) pronounced on 6th December 1985 at Moscow Seminar on the studies of time in natural sciences at Moscow University. V.V.Nasonov has been an active participant of N.A.Kozyrev’s experiments and his closest co-worker. As marked by N.A.Kozyrev, “V.V.Nasonov’s work imparted a high degree of reliability to the experiments...” (Kozyrev 1971, p.119).

“A resistor placed near a common laboratory process, such as acetone evaporation from a piece of cotton wool, sugar dissolving in water, etc., exhibited a relative resistance variation in the sixth or fifth significant figure, or even in the fourth one for a resistor with an especially high temperature coefficient” (Kozyrev 1982, p.62).

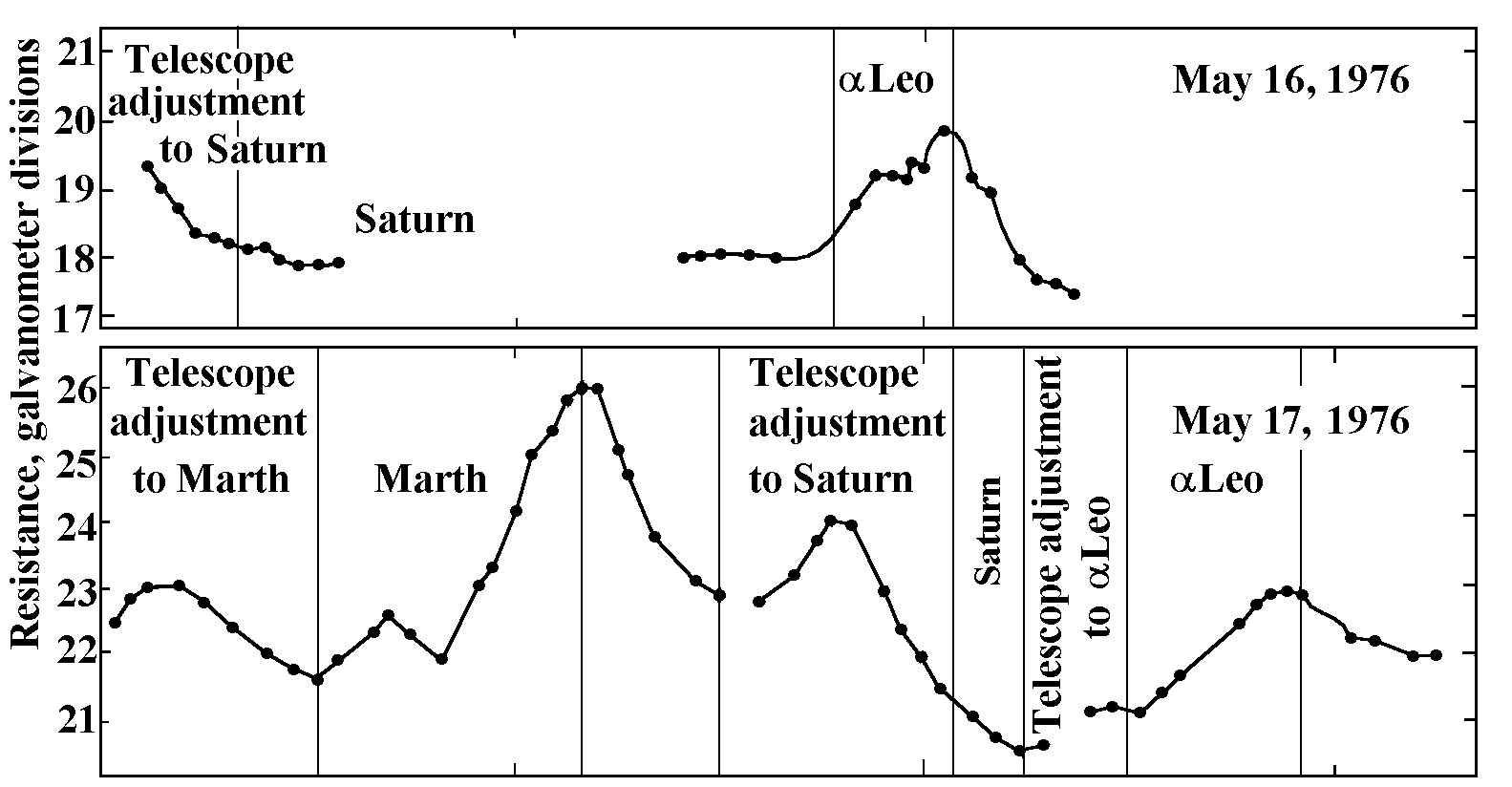
“... A simple physical system was found... resting on variations of... electrical resistance in conductors. These variations were registered... by a galvanometer in a Wheatstone bridge circuit. In order to observe the maximum bridge sensitivity condition, all its four resistances were taken equal to the galvanometer internal resistance... The bridge was fed by a stabilized voltage of 30V, so that a single galvanometer scale division corresponded to a resistance variation of 1.4·10^-2Ohm, which makes a fractional variation of 3·10^-6. To double the effect, the resistors, being posed crosswise in the circuit, were placed side by side, forming two couples, each occupying the area of 15ґ15mm².

To avoid temperature impacts, the resistors were placed in a cardboard tube with wooden stoppers, put into three duraluminium tubes, each with duraluminium lids. Openings of 15mm in diameter were drilled in the metal tubes against the couples of resistors and glued up with paper. In these conditions the galvanometer counts were stable enough even in the tower of the telescope. All the processes emitting time caused resistance reduction, while the opposite processes raised it within a few scale divisions, corresponding to fractional changes of 1 to 10ppm” (Kozyrev 1977, pp.222-223). Let us make things clear following Kozyrev (1977, pp.214-215): “The processes increasing entropy where they are happening, emit time. These are, for instance, ice melting, liquid evaporation, dissolution of substances in water and even plant withering. The contrary processes, such as cooling of bodies and water freezing, absorb time...”. “Astronomical observations with that instrument were carried out on the MTM-500 telescope in 1976. The image of a star was projected onto the paper of one of the openings of the tube. As usual, the stellar light was removed by a thin shield. Figure 3 depicts the results of three nights of observations... The figure shows that Saturn did not cause any effect, as it has been the case in measurements with a torsion balance... Unlike that, the star aLeo, in accord with the previous observations, exhibited a distinct effect on the instrument. Mars, like other Earth-group planets, yields a variable effect...” (Kozyrev 1977, p.224).

“The difference between a star’s true and apparent positions allows one to calculate its parallax provided the proper motion is known. The corresponding observations were carried out in October 1977 at the 50-inch reflector of Crimean astrophysical observatory. The impact of time was detected by resistor electric conductivity changes... The observational results are presented in Table 1 where the observed true stellar position displacements are compared with the pre-calculated ones. Scanning of the Moon by this method showed a high activity of the crater Alfonce just at the place where a gas outflow happened on 3 November 1958. The inner slope of the Aristarch crater also reveals an active center” (Kozyrev and Nasonov 1978, p.168).

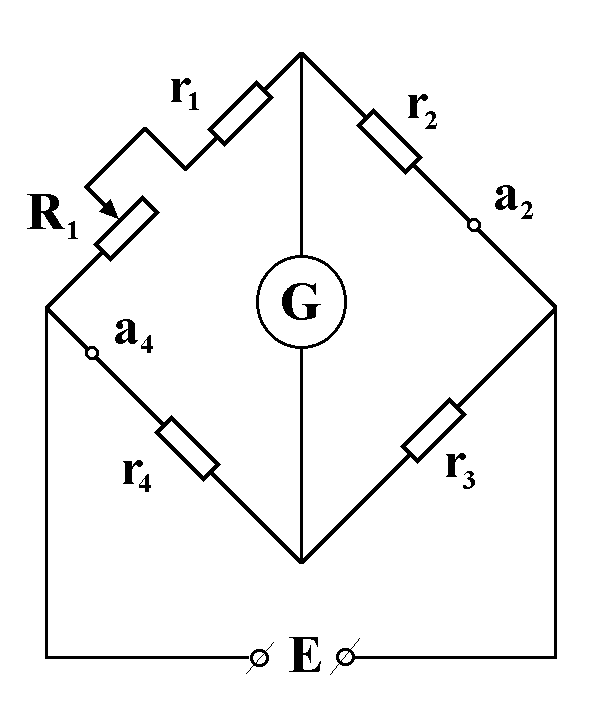
The Wheatson bridge was built on the basis of metal-film resistors r₁, r₂, r₃, r₄ (Fig.4) ... with the resistance of 5.6kOhm, having a positive temperature coefficient of 1.5´ 10^-4 ... To equalize the bridge arms a resistance box was joint to the input near the power source... Laboratory experiments showed that the galvanometer count stability is significantly improved if one places several plates of aluminium of several cubic centimeters total volume, in the way shown in Fig.4 (a₂ and a₄)... (Kozyrev and Nasonov 1978, pp.172-173).

“The above methodology was used with no significant changes in spring... and autumn... observations of 1978 (see Table 1). During the autumn observations the bridge system experienced certain improvements. The bridge resistors, taken with large temperature coefficients, were well selected by the values of the resistance and the above coefficient. The system turned out to be well stabilized, which allowed us to remove the aluminium plates from the circuit... and raise the voltage from 30 to 60V. That resulted in sensitivity increase by nearly an order of magnitude” (Kozyrev and Nasonov 1980, p.77).

N.A.Kozyrev’s experiments with metal film resistor probes have been repeated in recent years. Not a single fact in contrast to Kozyrev’s observations of stellar action-at-a-distance upon a resistor, has been discovered (Lavrentyev, Yeganova et al. 1990). An action of the Sun’s true position upon a resistor placed in the focal plane of a reflecting telescope, has been discovered (Lavrentyev, Gusev et al. 1990). Numerous nontrivial anomalies were also discovered in starlit sky scanning using Kozyrev’s metal-film resistor probe in a special receiver system (Lavrentyev et al. 1992).

Table 1. Astronomical object displacements in arc seconds, observed due to active properties of time and calculated using Genkins’ Catalogue of Trigonometric Parallaxes. Errors, being equal to differences between observations and calculations, are of the order of 2ґґ-3ґґ, i.e., of the order of slit width (Kozyrev and Nasonov 1978, 1980).

“Two photocells, as identical as possible, were mounted at the inner sides of the lids closing a tube, in whose middle an electric torch lamp was inserted through an opening. The plus of one photocell was joined to the minus of the other, with a galvanometer included between these connections... with sensitivity of 2´ 10^-9A per division. A perfect identity of photocell operations, such that the galvanometer showed no current, was achieved by adjusting an f-stop of the applied lamp light. In these conditions the galvanometer showed that the photocell operation is indeed changing when a certain process takes place in its neighborhood. The galvanometer deflections have been observed to be of a few scale divisions. Hence, a solar battery photocell current being about 1mA, the fractional photocell operation change was about 1 to 10ppm... All the processes repelling the torsion balance pointer and emitting time, weakened the photocell operation, while those absorbing time, favoured its work” (Kozyrev 1977, p.222).

“One more system was investigated in the laboratory, the one relying on varied quartz plate elasticity due to oscillation frequency variation. Oscillation frequencies of two such plates, each placed in a separate evacuated housing, with eigenfrequencies of about 11MHz, were compared. It turned out that processes emitting time cause an oscillation frequency increase of about 1 Hertz, i.e., a fractional change of about 0.1ppm. However, this system turned out to be very unstable and it proved to be too difficult to apply it in practice” (Kozyrev 1977, p.224).

2.5. Mercury thermometer

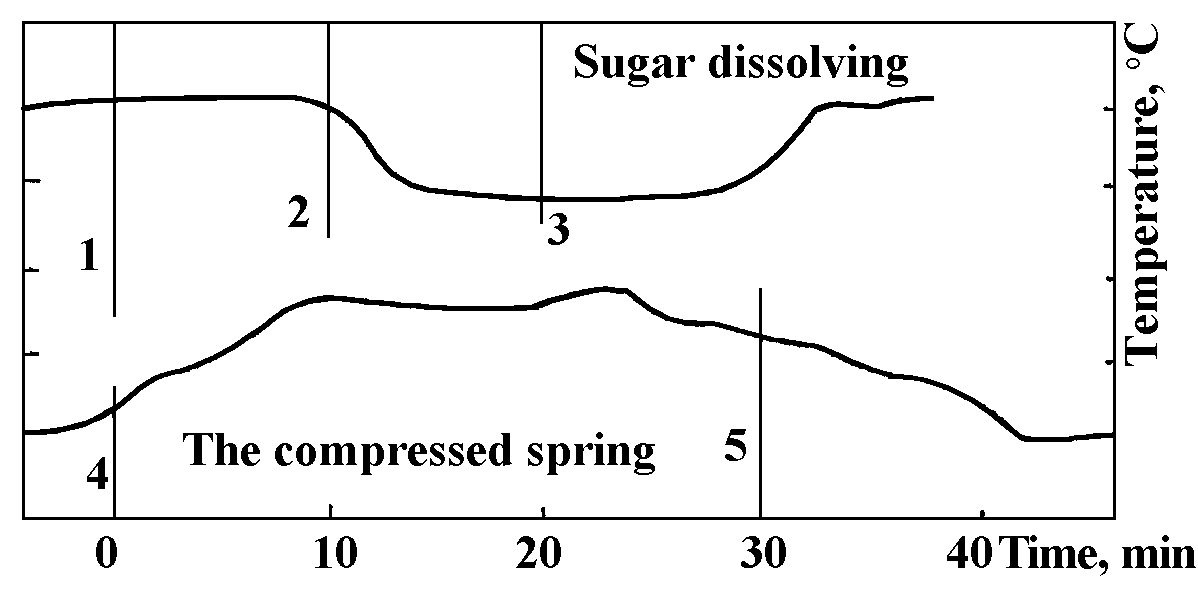
“Studying the effect of time on resistor electric conductivity, we used acetone evaporation at spacing of 10 to 15cm from the resistor under study as a standard process. However, the evaporation process could also affect the resistor... in the most trivial way, i.e., by lowering its temperature during the evaporation. In order to take into account the cooling effect, we made an attempt to measure directly the temperature variations near the evaporating acetone by Beckmann’s mercury thermometer with sensitivity of 0.01°C per scale division. The first experiments, with lacking thermal protection, revealed a temperature decrease of several hundredths of a degree, sufficient to account for all the observed resistor conductivity variations. However, even when the resistor had been thermally protected, the thermometer continued to show the same temperature decrease. This circumstance, surprising at the first sight, showed that the thermometer responded not to temperature variations but to time emission due to acetone evaporation, which... made mercury compress. Further experiments, carried out with due care, confirmed this conclusion. The cardboard tube, enveloping the part of the thermometer with a mercury reservoir, was covered with cotton wool and placed in a glass flask. The process under study was carried out near the flask, while the height of the mercury column in the capillary tube was read on a temperature scale from another room, through a closed window. The height decreased when sugar was dissolved in water of settled temperature and increased when a previously compressed spring was placed near the thermometer (Fig.5)... The fractional mercury volume and density changes turned out to be of the same order of magnitude as the resistor conductivity variations...

Beckmann’s thermometer ought to respond to astronomical phenomena as well, although it is quite certainly impossible to use it in a telescope tower. However, one could hope that in a close room with stable temperature it will be possible to detect its response to such intense phenomena close to the Earth as a lunar eclipse. During an eclipse the lunar surface experiences very rapid (for about a hundred of minutes) cooling from 100°C to -120°C and heating to its former temperature. The first process is accompanied by time absorption..., so that it should not manifest itself on the Earth in an appreciable way. On the contrary, the second process is accompanied by time emission, able to be detected by a sufficiently sensitive instrument on the Earth. Such observations have been carried out with Beckmann’s thermometer during a partial (but with a big phase, F = 0.86) lunar eclipse...

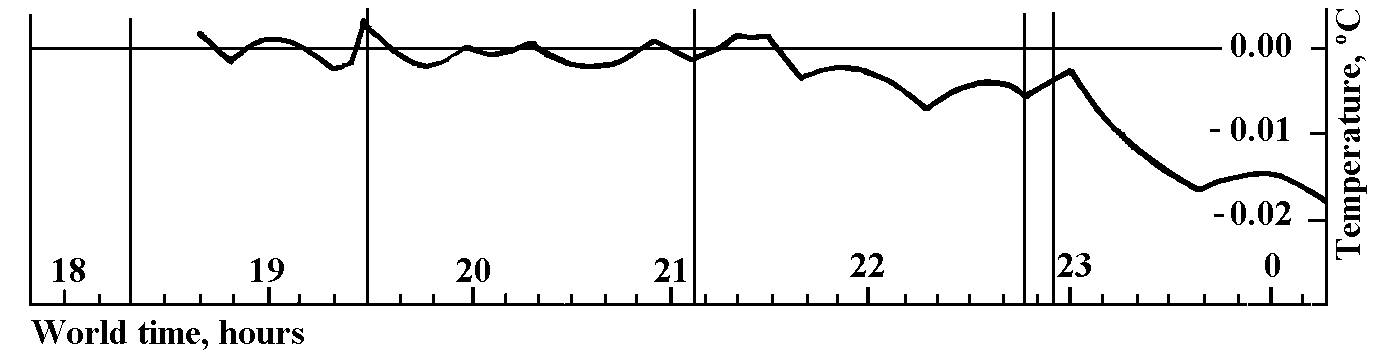
During the eclipse... the thermometer was in sufficiently stable conditions of a semi-basement room. The thermometer readings were taken every 5 to 10 minutes... The corresponding graphs of Fig.6 show that those readings started to change indeed only after the maximum eclipse phase was gone, i.e., when the parts of the lunar surface freed from the Earth’s shade, started to be heated” (Kozyrev 1982, pp.63-65).

“...Since a resistor has a big active layer area,... it does not allow one to achieve high measurement accuracy... so there was a necessity to create detectors able to raise the measurement accuracy by an order of magnitude. Moreover, the considerable resistor inertia prevented automated measurement result recording to be provided when using the bridge circuit.

A lengthy search of such detectors finally led us to systems with contact pairs of two metals to be used as probes. Copper is the basic metal in all such couples,... while its partner is a metal which can be used as a superconductor (niobium, lead, tin). The best results in laboratory operation have been shown by the couples of tin and copper...; the corresponding automated record for the star aBoo was obtained in 1981 (Fig.7)” (Nasonov 1985a, p.17).

“Laboratory measurements were carried out by the following method. A contact pair, with the contact area of 0.02mm² and a tin insert 15cm long (its resistance equals 0.55Ohm), was located at a height of 5cm over a laboratory table. It was protected from external influences by a closed envelope of plate packages, with the screen-free facial part of the closed volume covered by two layers of Whatman paper. The process action (acetone evaporation from a piece of cotton wool) was executed from the distance of 10cm. The amount of acetone was no more than 4 or 5 drops. The second contact of the system was shielded by a system of aluminium-coated flat mirrors. The two tin-copper contacts were spaced by 12cm. The natural thermal emf due to room temperature gradient at contact locations was about a few microvolts. Prior to an experiment, the system was kept in operation until the recorder showed a fully stable signal. Then the source of action was established and the changes happening in the system as a result of acetone evaporation, were recorded (Fig.8).

...The time needed for a full manifestation of causal interactions in our systems is within 5 to 20 minutes. As shown by the graphs, the optimum time for an effect to show itself is about 10 minutes. The process having stopped its action on the detector, the measurement system returns to its starting position. The whole experimental cycle, i.e., one measurement, lasts 30 to 40 minutes” (Nasonov 1985b, pp.16-18).

2.7. Substance

Under the action of liquid nitrogen evaporation “water viscosity was measured by a viscometer of VPZh-2 type. In the first run of experiments the temperature dependence of kinematic viscosity of deionized water was obtained, because one could suspect a purely thermal influence of liquid nitrogen evaporation on the object under study. As one could expect, water viscosity increased with decreased temperature. In the second run we investigated a direct action of liquid nitrogen evaporation on deionized water viscosity... Kinematic viscosity was measured directly during the action. The measurements showed that in 10 to 15 minutes after the action, water viscosity abruptly decreased by a value of about 3%. The fact that the viscosity just decreased, shows that the action had nothing to do with a thermal influence of the source of action, since water viscosity increases due to temperature decrease. Further on the viscosity value remained steady at the same level... The decreased viscosity value took on by water restored to its usual value in approximately a day” (Danchakov 1984, pp.111-112).

“We use such irreversible process sources as liquid nitrogen evaporation at room temperature, dissolution of mixed (commercially available) sugar and sorbite in water, boiled water cooling and other processes of physical and chemical nature and also metabolic processes of a human body in a stable condition of its functional characteristics... We have fixed the fact that distilled water density responses to the above irreversible processes...

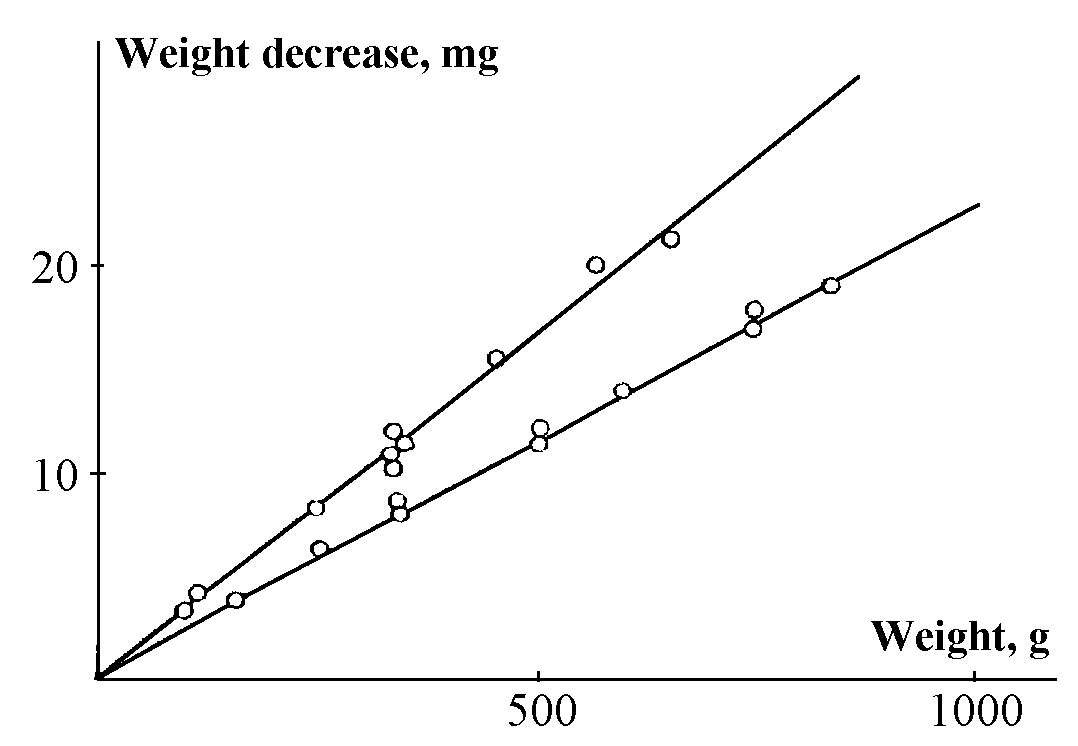
We studied the responses of substance mass to external irreversible processes, using the objects of duraluminium, copper, brass, quartz, glass, quartz flasks filled with air ... and many others... The fractional mass variation effect Dm/m was found to be 1 to 10ppm, i.e., more than an order of magnitude weaker than the fractional distilled water density variation” (Lavrentyev et al. 1991, pp.635, 637).

“We chose as an object to be studied the interaction reaction of potassium permanganate KMnO₄ and the organic impurities in rectified spirit, the one well-known to specialists. The process can be followed visually by color variation and precipitation intensity. A 4 per cent KMnO₄ solution was prepared. Five milliliters of that solution were added to 100ml of rectified spirit (96%). The starting mixture having been prepared, an experimental group of test tubes was subject to a direct action of the liquid nitrogen evaporation process... for forty minutes. In all other respects the experimental group and the reference one were kept in equal conditions. The reaction process was observed for 24 hours. The reaction began immediately in the reference test tubes. Mixture lightening, flake formation and precipitation took place monotonically to the end of the experiment. As compared with the reference ones, in the experimental tubes the reaction proceeded slower within the first 45 minutes. Later the picture changed to remain steady until the experiment was over, namely: the lightening and precipitation rates were higher in the experimental tubes than in the reference ones, so that when precipitation in the experimental tubes was over, it could still be observed in the reference ones” (Danchakov 1984, pp.117-118).

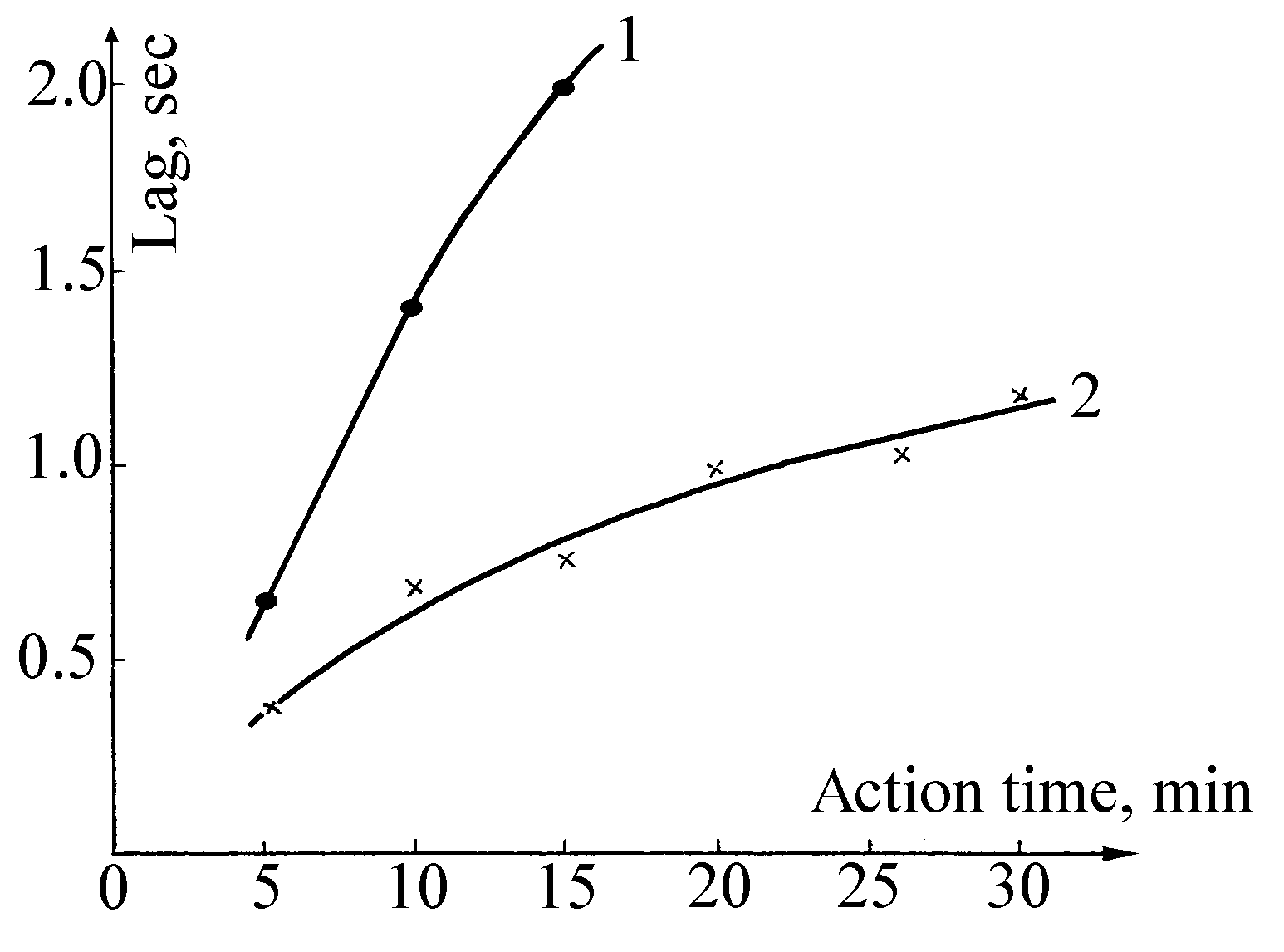
“We are dealing with torsion balances which are present in instruments measuring time... They are formed by a combination of a tiny flywheel and a spiral spring... Such a balance is a mechanical resonant system whose elasticity is determined by the spring and the moment of inertia by the flywheel... It seemed reasonable to use a clock mechanism in order to test the impact of the liquid nitrogen evaporation process on the balance spring... The parameter reflecting the existence of action, would be spring elasticity. Since elasticity determines the oscillation period, the result could be obtained in a numerical form from a comparison between a clock under experiment and a reference one. We used in our experiment a Raketa wrist watch and a class II two-handed, type C-II-1b stopwatch. There were 2 watches of each type, one for experiment, the other for reference. Prior to each experiment, the readings of the experimental and reference watches were compared for 45 minutes. No essential deflections were observed: the readings coincided. Figure 9 shows the average results of repeated experiments. We see that the experimental watches are markedly slow as compared with the reference ones during the action. After a 15 minutes’ action the experimental “Raketa” watch was 2 seconds behind the similar reference watch. The experimental stopwatch under the same conditions was only 0.7 second slow. The lag of experimental watches indicates their balance period increase, which in turn means their spiral spring stiffness reduction. One could notice that a lowered temperature would create a contrary picture... It is of interest to note that in 48 hours after the action all the experimental watches restored their rates” (Danchakov 1984, pp.119-120).

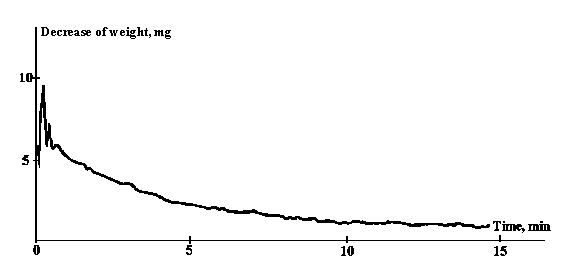
“... An inelastic collision should cause... weight decrease... Even the first experiments showed that body collisions resulting in irreversible deformations were indeed accompanied by their weight reduction. Bodies with masses up to 200 grams were weighed using an analytic balance with sensitivity of 1.4mg per division... A first class technical balance, with sensitivity of 10mg per division, was used for weighing heavier bodies (up to 1kg) and for control. These experiments showed that the weight defect does not disappear immediately after a collision but decreases gradually, with relaxation times of about 15-20 minutes... In further experiments a stiff elastic body (a ball bearing) was weighed after a collision with an inelastic (lead) plate and, conversely, lead was weighed after a collision with a stiff basement (stone floor). Later some experiments were carried out, consisting in weighing a deformable box after many abrupt shakes of stiff bodies confined in it and, conversely, lead shot was weighed after shaking it in a stiff box. Both the weight of a box with all its content was determined and separately that of a box and that of its content. The experiments showed that only the body which experiences the irreversible deformation process, loses its weight. Figure 10 shows, as a typical example, a graph of weight lessening of a 108g tin box after multiple shake of steel balls confined in it. The weight lessening... is plotted in milligrams along the ordinate axis, while the abscissa plots weighting time elapsed from the instant of force exertion on the box. Weight restoration, though somewhat incomplete, occurred here and in other experiments in about twenty minutes. The remaining small deflection from the initial weight disappears only after some ten hours. The complete balance readings restoration confirms the purity of the experiment and also indicates the reality of the observed weight loss...

Unlike that, reversible deformations do not cause body weight variation. Thus, compressed rubber or compressed steel springs exhibit their usual weight... It turned out that heating of bodies leads to a very significant loss of their weight” (Kozyrev 1984, pp.94-95).

I would like to note that an interpretation of inelasticity in the weight loss effect is somewhat ambiguous. The same effect is achieved when a body is subject to certain actions with no inelastic deformation: “A weight, suspended elastically, was removed from a balance and shaken up to 30 times vertically by hand. Then it was suspended by the balance again, the balance was let damp and its readings were recorded consecutively. It was discovered that after shaking the load on a rubber... an additional force... emerges. This experiment was carried out with different loading materials. Each of the materials showed its own value of the effect, certainly under the same experimental conditions” (Nasonov 1985a, p.15). See also a quotation from N.A.Kozyrev’s work (Kozyrev 1971) in Section 3.4 of this chapter.

Rotating bodies have been the first experimental objects for which N.A.Kozyrev and his colleagues discovered effects unable to be explained by the schemes of traditional physics. In order to exhibit effects of that kind, a rotating body should take part in some additional motion. In N.A.Kozyrev’s experiments those have been vibrations, falling in the Earth’s gravitational field, electric charge motion due to a current passing through the body, or an additional motion of atoms due to heating.

Gyroscopes. “Imagine a gyro in an envelope with a vertical axis being weighed on a beam balance... Vibrations are extremely advantageous in the experiments since their action is time-averaged to zero, so that from the classical viewpoint they cannot introduce forces which would act in a constant direction” (Kozyrev 1963, pp.104-105). “...Vibrations create a new zero point, with respect to which there happens weight lessening due to counter-clockwise rotation and quite an equal weight increase due to clockwise rotation (DQ = ±4mg)” for a gyro of 4.6cm diameter, Q = 90g weight and u = 25m/s rotation velocity (Kozyrev 1971, p.120). The fractional weight variations turns out to be proportional to linear rotation velocity of the body:

DQ/Q = u/c₂,

where c₂ is Kozyrev’s velocity-dimensional constant. N.A.Kozyrev treated c₂ as the “cause to effect conversion rate”, a universal constant, independent of body properties (Kozyrev 1963, p.98). Just the existence of such a universal constant makes it possible to connect theoretically the observed rotational effects with the existence of a certain substantial flow to be identified with the Kozyrev flow. By the formula of Section 1.3 of the author’s chapter in the first volume of the present book, the equation of metabolic motion can be written in the form , where the quantity is expressed in terms of the numbers of elements (n) and pre-elements (m) being replaced in an object in its metabolic motion. Thus just the pre-element replacements lead to the additional non-Newtonian force emerging; those non-Newtonian forces are proportional to the Newtonian ones and to mechanical motion velocity of the system.

Gyro vibrations took place both “due to rotor beating in bearings with a certain backlash” and in a system where the balance beam support was attached to a metal plate, whose end was lying on a ball bearing set eccentrically on an electric motor axis. This made it possible to obtain harmonic oscillations of any frequency and magnitude (Kozyrev 1971, pp.120,122).

“Imagine a gyro with a horizontal axis suspended like a pendulum by a thin filament. When the rotor vibrated in the bearings,... the pendulum was observed to deflect to the side (along the gyro axis) from which the rotation was seen counter-clockwise... In the pendulum experiment... it was easy to bring the source of vibrations to the suspension point... An aircraft automation gyro was used in the experiment, having the following characteristics: rotor diameter D = 42mm; rotor weight Q = 250g; envelope weight a = 150g. It was suspended with a horizontal axis position by a wire, 0.15mm in diameter and 330cm long, to a plate of a steadily mounted vibrator (an electromagnetic relay). Changing its feeding current frequency, one could create any vertical vibrations of the suspension. When the source of vibrations is situated at the suspension point, the pendulum is shifted along the gyro axis to the side from which the rotation is seen to occur clockwise” (Kozyrev 1963, pp.105-106). “Table 2 lists the numerous gyro linear displacement measurements with respect to the plumb line... The table shows that the effect is indeed proportional to the velocity of rotation. The ratio of DQ to the gyro full weight, being taken for the velocity u = 40m/s, is 3.6·10^-5. To obtain the ratio DQ/Q it is necessary to correct the above value by taking into account the envelope weight, i.e., one should divide it by (Q+a)/Q. Special experiments with purposely increased envelope weight showed that such a correction is indeed necessary. The result is that... c₂=700km/s” (Kozyrev 1958, pp.78-79).

A whole series of recent works is dedicated to attempts to detect rotating gyro weight variations. It should be noted that apparently none of the authors mentioned below was aware of Kozyrev’s work as well as those of his followers. Japanese experimentalists (Hayasaka and Takeuchi 1989) studied weight variations of 150 gram gyroscopes rotating by inertia, with no systematic error. The measurements showed that the weight variations are quite asymmetric with respect to rotations around a vertical axis: right rotation (the rotation vector points down) causes weigh decrease of a few milligrams, proportional to rotation frequency within 3000 to 13000 RPM. However, a left rotation causes no weight variation. The following possible causes of systematic errors are investigated in the paper: gyro dynamic characteristic differences for the two rotation directions; differences in its electromagnetic interaction; different friction in bearings, depending on rotation direction; environmental variations during the repeated experiments; differences in inertial forces; differences in the interaction of the Earth’s and gyro rotations.

American (Faller et al. 1990, Nitschke and Wilmarth 1990), French (Quinn and Picard 1990) and other Japanese (Imanishi et al. 1990) researchers did not confirm the results of Hayasaka and Takeuchi (see some arguments in Section 1 of this chapter).

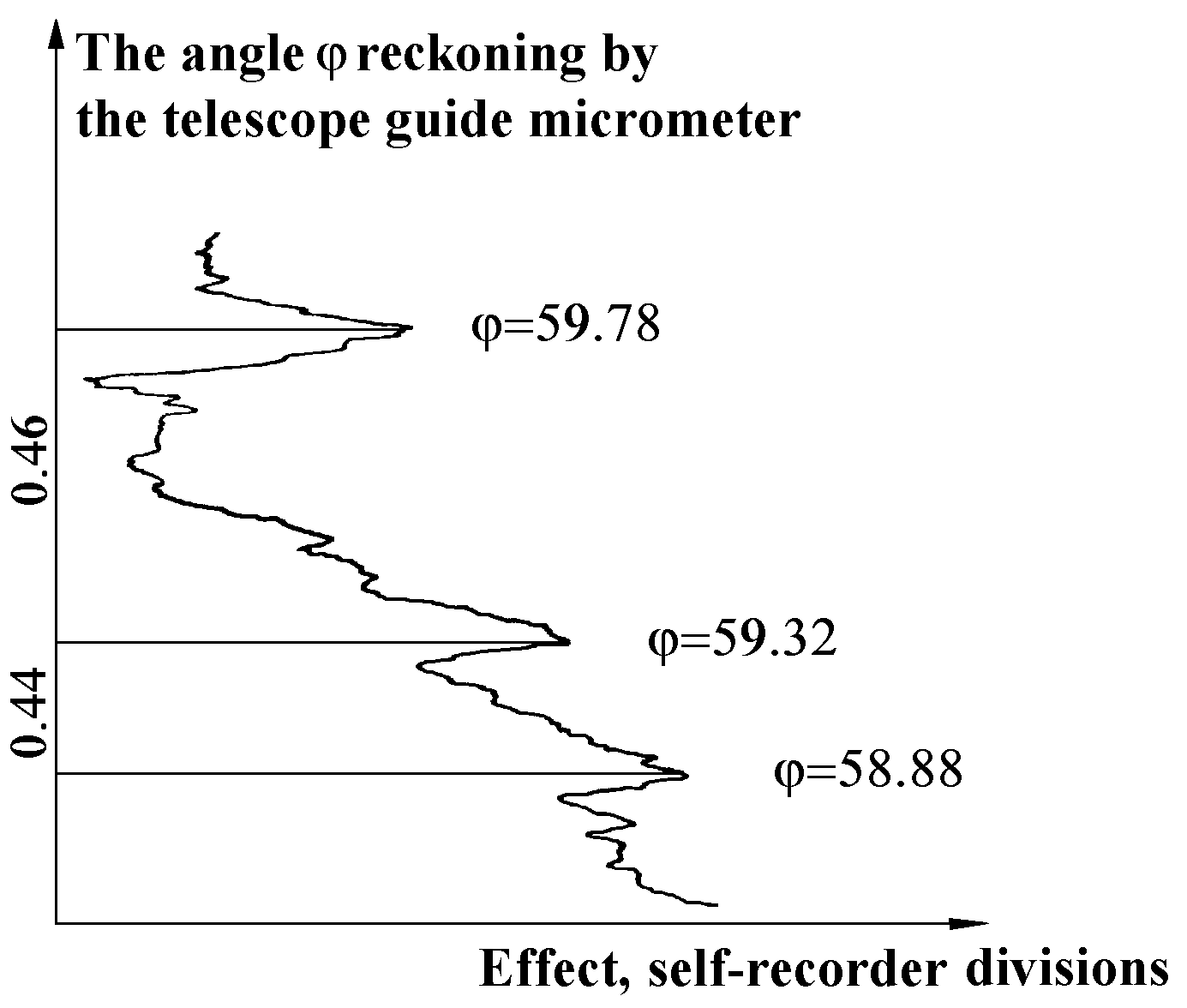
Bodies rotating with the earth. “The Earth’s rotation allows very simple and easily realizable experiments to be organized” (Kozyrev 1977, p.213). One of Kozyrev’s early papers (Kozyrev 1958) describes in detail the experiments on anomalous southern deflection of bodies falling in the Earth’s gravitational field, from Hooke’s experiments of 1680 to that of Kozyrev, arranged at Pulkovo.

The northern deflection effect “is observed by vibration of any nonrotating body suspended to a filament. The conditions necessary for obtaining the pendulum displacement effect due to the Earth’s rotation, are quite similar to the above conditions of gyro displacement... These experiments were carried out at Pulkovo with pendulums of different lengths, from 1.5 to 11 meters. The fractional displacement turned out to be independent of pendulum length... Thus the displacement is caused by a certain force, independent of pendulum construction. This force significantly varies with geographic latitude... No doubt, the forces measured by pendulum displacements are horizontal projections of asymmetric forces active at the surface of the Earth. As for vertical projections of the same asymmetric forces, one can try to obtain them by vibrating the system with a vertical degree of freedom” (Kozyrev 1963, p.107). “The simplest system of this kind is a beam balance. Assume that a weight is suspended at one end of the beam by a rigid suspension able to transfer beam vibrations to the weight. The other, balancing weight was suspended to rubber shock-absorbers which damp all the oscillations. Then, as the balance vibrates, it is possible to observe oscillating weight reduction...

The experiments showed that a weight reduction of a rigidly suspended body, as well as a displacement in experiments with a pendulum, happens stepwise, beginning with a certain vibration amplitude... Numerous repeated weighing allowed the weight reduction to be measured to several tenths of a milligram. Figure 11 depicts the results of these experiments carried out at Pulkovo and in the Botanical gardens in the city of Kirovsk... The weight reduction turned out to be proportional to the weight itself. The angular coefficient of these graphs yields... the vertical component of the vector. By these values combined with those of the horizontal components... it is possible to determine the vector’s slope against the horizon...” For Pulkovo the true latitude is 59°46ґ and the calculated one is 59°32ґ; the same values for Kirovsk are, respectively, 67°39ґ and 67°58ґ, showing convincingly that there is a real coupling of these forces to the Earth’s rotation (Kozyrev 1958, pp.65-68).

“Initially in the experiments involving vibration the latter was excited using an electromagnetic relay attached to the balance beam support. This resulted in complicated oscillations with noise containing no simple harmonics. The sought effect was achieved only at certain choices of frequency and magnitude. The experiment was essentially improved by introducing harmonic oscillations with the aid of a ball bearing set eccentrically on an electric motor shaft. It became very easy to achieve the effect under such oscillations” (Kozyrev 1963, p.108). Kinematics of the beam balance experiment could also be changed: “In our experiments one of the weights was suspended rigidly by a wire, the other by an elastic rubber or a spring. As the support vibrated, the beam end with the rigidly suspended weight remained practically at rest. Therefore its other end, that with an elastic suspension, oscillated with a double amplitude as compared with the middle. It turned out that, beginning with a certain vibration acceleration, the balance deflects abruptly to a certain value, indicating a larger weight of the load suspended elastically” (Kozyrev 1963, p.107). “The predicted sign alteration, happening when the weight itself became source of oscillations, was verified. For that purpose the beam support was placed on a rubber spacer and a rubber-suspended weight was replaced by a rigidly suspended electric motor with an eccentric which caused the increase and decrease weight. The whole beam kinematics remained the same. However, the system suspended from the oscillating beam end, became lighter, contrary to the previous experiment. This result entirely rules out any classical explanations of the observed effects...” (Kozyrev 1971, p.126).

Other processes connected with Kozyrev’s flow emission, also exert influence on the weight-changing effect for the bodies rotating with the Earth. “Observations of a beam balance subject to vibrations have been carried out at Pulkovo during five solar eclipses... All the observed eclipses caused a decrease of the forces due to the course of time. Figure 12 exemplifies such observations...” (Kozyrev 1977, p.215).

The engineering details of N.A.Kozyrev’s experiments are described in his special paper (Kozyrev 1978), along with a proof of the fact that a possibility of weight variations observed in the experiments with a balance is entirely ruled out by classical mechanics.

“The vibration experiments have a shortcoming related to the fact that vibrations always violate the correctness of measurement system operation to a certain extent... Therefore it is highly desirable to find some other method... One could, e.g., pass a steady electric current through a long metal wire by which the body of the pendulum is suspended. The current could be entered through the suspension point and passed along a very thin wire near the body of the pendulum failing to hinder its oscillations. The Lorenz forces due to current interaction with the Earth’s magnetic field act in the plane of the first vertical and cannot cause a meridional displacement of interest for us. These experiments have been successful. Thus, a pendulum 2.8m long, with a voltage minus applied to the suspension point, exhibited a stepwise southern deflection of 0.024mm, beginning with the voltage of 15V and the current of 0.03A. This deflection was preserved by voltage increase up to 30V... The voltage plus being applied to the suspension point, a similar northern deflection occurred” (Kozyrev 1971, p.127). It turned out that the necessary motion of the pendulum atoms, supplementary to their rotation with the Earth, “could be detected still simpler by heating or cooling the suspension point. For this purpose the pendulum should be suspended by a well heat-conducting metal wire. The suspension point was heated by an electric spiral. The spiral being heated to shine, the pendulum deflected (to the South)... Cooling the suspension point by dry ice caused a northerly deflection. A southern deflection could also be obtained by cooling the body of the pendulum, e.g., by placing it in a vessel with dry ice on the bottom” (Kozyrev 1971, p.127).

Planets as gyroscopes. “Rotating celestial bodies involve an interaction between the rapidly rotating equatorial masses and slowly rotating masses near the axis. Most of the planets of the Solar system rotate counter-clockwise as viewed from the North pole... thus the equatorial masses must be subject to forces directed to the North. The masses situated near the rotation axis, must be subject to the same forces directed to the South. Evidently both hemispheres of the Earth contain a parallel where the causal forces are zero. The Northern hemisphere should be more compressed due to the additional forces as compared with the more convex Southern hemisphere. The planet figure will be thus asymmetric with respect to the equatorial plane... a meridional section of the planet forming a cardioid impressed from the North and sharpened to the South. The existence of the Antarctic continent and the Northern polar basin, combined with the preferred continent location in the Northern hemisphere indicate such a cardioidal shape of the Earth. This circumstance could be hardly accidental, since an action of weak forces violating the symmetry could create a preferred direction for the processes happening inside the Earth” (Kozyrev 1958, pp.49-50, 54).

“The asymmetry coefficient h is defined in the following way:

,

where a is the major semiaxis, while b_S and b_N are the distances between the poles and the equatorial plane. A thorough investigation of Jove’s figure carried out by many photographs by the author and D.O.Mokhnach, showed that Jove’s southern hemisphere is more stretched, and the asymmetry coefficient was obtained to be (3±0.6)·10^-3. A similar result with lower accuracy has been obtained for Saturn: h = (7±3)·10^-3. Nowadays there are certain data indicating that the Earth’s Southern hemisphere is also more stretched than the Northern one. For an asymmetric homogeneous body the force of gravity should be greater at the obtuse end, i.e., at the Northern one... The existence of just this difference... has been known for long: Dg/g=3·10^-5. The observed satellite motions... have shown that the perigee distance in the Northern hemisphere is much less than that in the Southern one. This directly implies that the force of gravity is greater in the North hemisphere of the Earth as compared to the Southern one, in line with the measurements carried out on the Earth’s surface. Judging by the literary data, the satellite motion details also confirm the cardioidal form of the Earth.

To avoid a misunderstanding it is necessary to note that the land-surveyors and satellite motion investigators arrive at a contrary conclusion based on the existing data, i.e., that the Northern hemisphere is more stretched. The essence of this divergence is that only the forces of gravity and the centrifugal forces are commonly taken into account. Such a consideration excludes the possibility of an asymmetry of a homogeneous body, so that the Dg found could be explained only by a dense matter excess in the Northern hemisphere. In such a case the equal-valued level surface should move further and one would obtain hemisphere stretching for greater gravity. However, the asymmetry sign obtained directly for Jove and Saturn, oppose that interpretation” (Kozyrev 1963, pp.103-104).

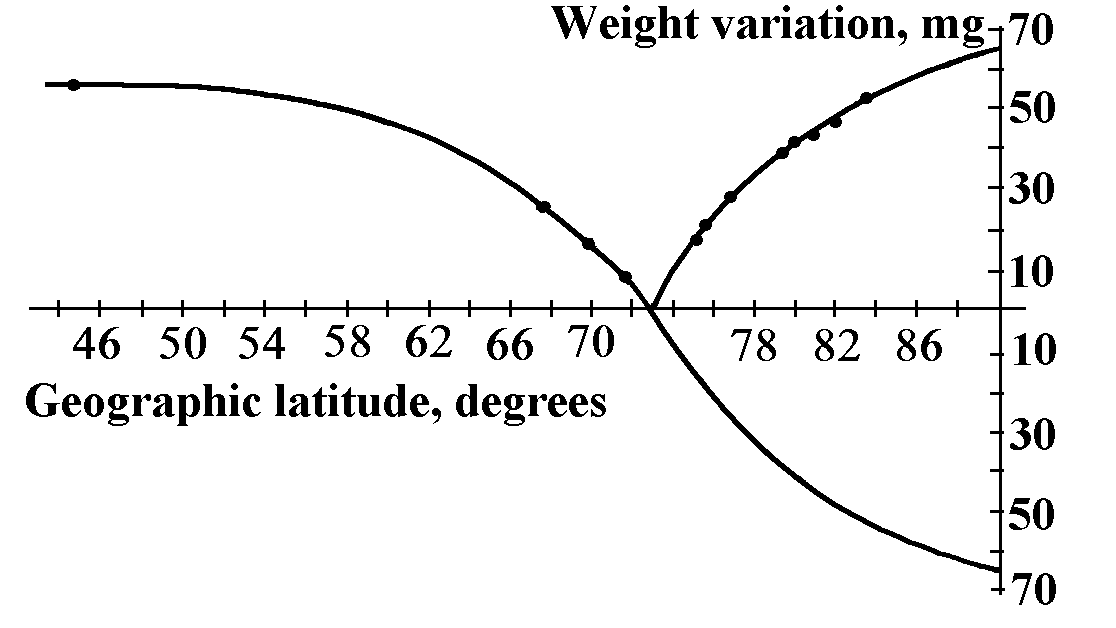
“The polar regions are of particular interest for studying the asymmetric force distribution on the Earth’s surface, since these are the regions of the parallel where these forces vanish and where they vary with latitude especially rapidly. The corresponding measurements have been carried out by N.A.Kozyrev and V.G.Labeish... They measured the vertical component of the asymmetric forces by weight increasing at an elastic suspension by balance vibrations. These measurements were carried out in Amderma, Tiksi, the Isle of Kotelny, Cape Cheliuskin, the Isle of Dixon and at some points on drifting ice with maximum latitude of 84°15ґ. The values of the asymmetric force vector magnitude was obtained by multiplying by cosecj. In Fig.13 these forces’ latitude dependence is plotted, expressed in fractions of the gravity force. The former determinations in the Crimea, Pulkovo and Kirovsk are also presented here... The curve shows that the zero asymmetric force parallel is somewhere near 73°...” (Kozyrev 1963, pp.109-110). “It is remarkable that the critical parallel obtained corresponds in the Northern hemisphere to the boundary of the continents and the beginning of the Arctic ocean depression while in the Southern hemisphere it corresponds to the parallel where the Antarctic continent rises” (Kozyrev 1958, p.68).

“One should expect the existence of a specific circulation in the planet’s atmosphere, a northerly tropospheric air mass transport and a southern counter-current in the upper layers. Such a circulation would lead to different climates of the hemispheres, so that the Northern hemisphere would become warmer than the Southern one. Such a climate difference actually exists. The annual temperature of the Southern hemisphere is 3°C less than that of the Northern hemisphere. Therefore the thermal equator is displaced by 10° to the North from the geographic one. Such a great climate difference could hardly be explained by only the Earth’s orbit eccentricity...

Along with the forces moving the air masses to the North, the opposite forces should exist, applied to the Earth’s surface. These forces are able to move the ocean surface to the South. The surface layer current complexity and variability make it a hard task to notice the preferred southern current direction. However, one can notice the inevitable northerly motion of deep-see counter-current by southern polar water penetrating to the North. Such a deep-see water motion indeed seems to exist in the Atlantic and Pacific oceans” (Kozyrev 1958, pp.69-71).

N.A.Kozyrev’s conception has created an unexpected explanation of a large variety of geophysical effects hardly explainable from the conventional standpoint: figure asymmetry, geological structure, atmospheric circulation and physical field distributions of the Earth and other planets (see the chapter by M.L.Arushanov and S.M.Korotayev in the present book). No doubt alternative explanations of the above geophysical effects also exist (see e.g. A.G.Parkhomov’s chapter in the present book about the Earth’s cardioidal shape).

“... It is the life essence that lacks in our scientific knowledge. Physics, chemistry and other exact sciences are able to accurately follow and predict the way of a dry leaf fallen from a tree and carried away by the wind, they can even write down its equation of motion, but they are helpless in explaining how it had grown, how it took its shape and properties. One cannot refer to specific properties of plants, absent in unanimate nature. Living organisms cannot create things absent in nature. They can only collect and use something from the general properties of the World. Consequently, those properties must be present in unanimate nature as well. And that is the place to search them since here one can employ the methodology of the exact sciences and their enormous experience of cognition” (Kozyrev 1975, pp.2-3). “The experimental results show that the organizing issue inherent to the active property of time, exerts a very small influence upon systems as compared with the common destructive course of development. Therefore it is not surprising that this life essence was missed in our system of scientific knowledge. However, being small, it is distributed everywhere in nature and only a possibility to store it is necessary, like that enabling the small drops of water falling to vast areas to maintain the continuous current of mighty river streams. Such a possibility is realized in organisms since the whole vital activity opposes the system destruction trend” (Kozyrev 1982, p.71).

“The course of time existing in the World, establishes the fundamental difference between the right and the left in space. It is wonderful that such differences of the right and the left indeed exist in nature and even catch the eye. These differences are known for long in the organic world. Animal and plant morphology yields a great number of examples of persistent, repeated and inherited asymmetry. For instance, mollusk shells are in an overwhelming majority of cases spiraled to the right. A certain dominating asymmetry of microbes is also observed, in particular as they form spiral structured colonies. The asymmetric organ positions of higher organisms are always repeated, so that, for instance, hearts of vertebrates are as a rule on the left side. Such an asymmetry also exists in plants as well, for instance, left spirals are preferable in conducting vasa.

In the middle of the last century Louis Paster discovered the asymmetry of protoplasm and proved by a number of remarkable studies that asymmetry is a basic feature of life. In inorganic nature stereoisomers form recemates, i.e., mixtures with equal numbers of right- and left-handed molecules. Unlike that, their numbers are radically different in a protoplasm. Thus, for instance, left-handed glucose practically cannot be consumed by an organism, left-handed nicotine is more poisonous than the right-handed one, etc. The asymmetry can have a physical meaning only if there exists time directionality” (Kozyrev 1958, pp.26-27).

“We chose liquid nitrogen evaporation as a source of action... In addition, we observed the action of the natural process of snow thawing... Actually two processes affected the object under study, the evaporation itself and nitrogen vapour warming... Among the objects to be studied there were microorganisms of the species Pseudomonas fluoresceins along with those of artesian water, oat and pea seeds... and the process of growing onions in water... By the existing views, ambient temperature deflections within ±1°C cannot essentially affect the life of biological objects. Nevertheless, the temperature stability requirements were enhanced to ±0.2°C... The influence of variable nitrogen concentration in the air was eliminated by permanent ventilation... and also by the fact that in most cases the objects under study had been placed in hermetically closed test tubes of ordinary glass.

The action period lasted, as a rule, 60 minutes... All the experiments were accompanied by reference ones, such that the reference objects were in the same conditions as the experimental ones but just were not subject to the action of nitrogen evaporation.

...The action of liquid nitrogen evaporation upon microorganisms... was characterized by drastic activity suppression during the first day of the experiment and subsequent tending to the corresponding normal level...

...The experiments with oat seeds led to an important result: while the reference group of seeds exhibited normal germination level of 60%, that of their counterparts subject to the action of liquid nitrogen evaporation turned out to be zero: all the seeds were lost. With these seeds two experiments were carried out, with 80 seeds used.

The experiments with pea seeds also yielded some results of interest. Six experiments were carried out with 600 seeds used. The average germination level was 92%. The average germination of the seeds subject to the action... turned out to be 62%, i.e., some of the seeds were lost (Fig.14).

In the next run the experimental group of seeds was not subject, as before, to the process action. The action was exerted on the water supplied to sprinkle the seeds. 60 seeds, divided into three equal groups, were used in this experiment... In all the groups the germination level turned out to be 100%... Sprinkling by water subject to... the action also resulted in an expressed development lag of the experimental groups as compared with the reference one.

The experiment with the germinated pea seeds being subject to liquid nitrogen evaporation process, was continued: an experimental group of seeds and the corresponding reference group were transplanted to open soil and stem growth was observed... On the fifth day the experimental plants which had lagged behind, overtook the reference group and later were significantly ahead of it. The maximum outstripping (up to 50%) was observed on the eighth day...

The experiments showed that living matter is markedly affected at a distance not only by such an intense process as liquid nitrogen evaporation, but also by snow thawing... Some healthy equal-sized onions with equal root system sprouts, were selected as the objects to be studied... A reflector (a cardboard sheet covered with aluminium foil) was mounted over the experimental group in such a position that those onions “could see” the reflection of outdoor snow lying infront of the window. To restore the equality of lighting conditions of the experimental and reference groups, the window glass near the reflector was glued up with sheets of writing-paper. The results are as follows. 50 per cent onions of the reference group got rotten, having developed no roots and released no arrows; the remaining onions of that group developed the root system very slowly, lagged in arrow release, the arrows being small in number and slowly growing. By the end of the experiment the arrow mean height was 150mm while water in the cans was turbid and had the specific smell of rotting. The experimental group behaved clearly different. A stormy root growth was observed from the very beginning. The roots filled the whole lower part of the cans. All the onions turned out to be viable. In the course of the whole experiment water in the cans was crystal-clear and had no smell. By the end of the experiment these onions had arrows 300mm long...

The above experimental material leads to the following conclusions.

Irreversible processes change the properties of the ambient matter by action at a distance.

Living matter is especially sensitive to these processes.

Biological objects subject to a short-term direct impact of liquid nitrogen evaporation exhibit in certain conditions not only entirely eliminated life function suppression after a time, but also their subsequent stimulation” (Danchakov 1984, pp.101-121).

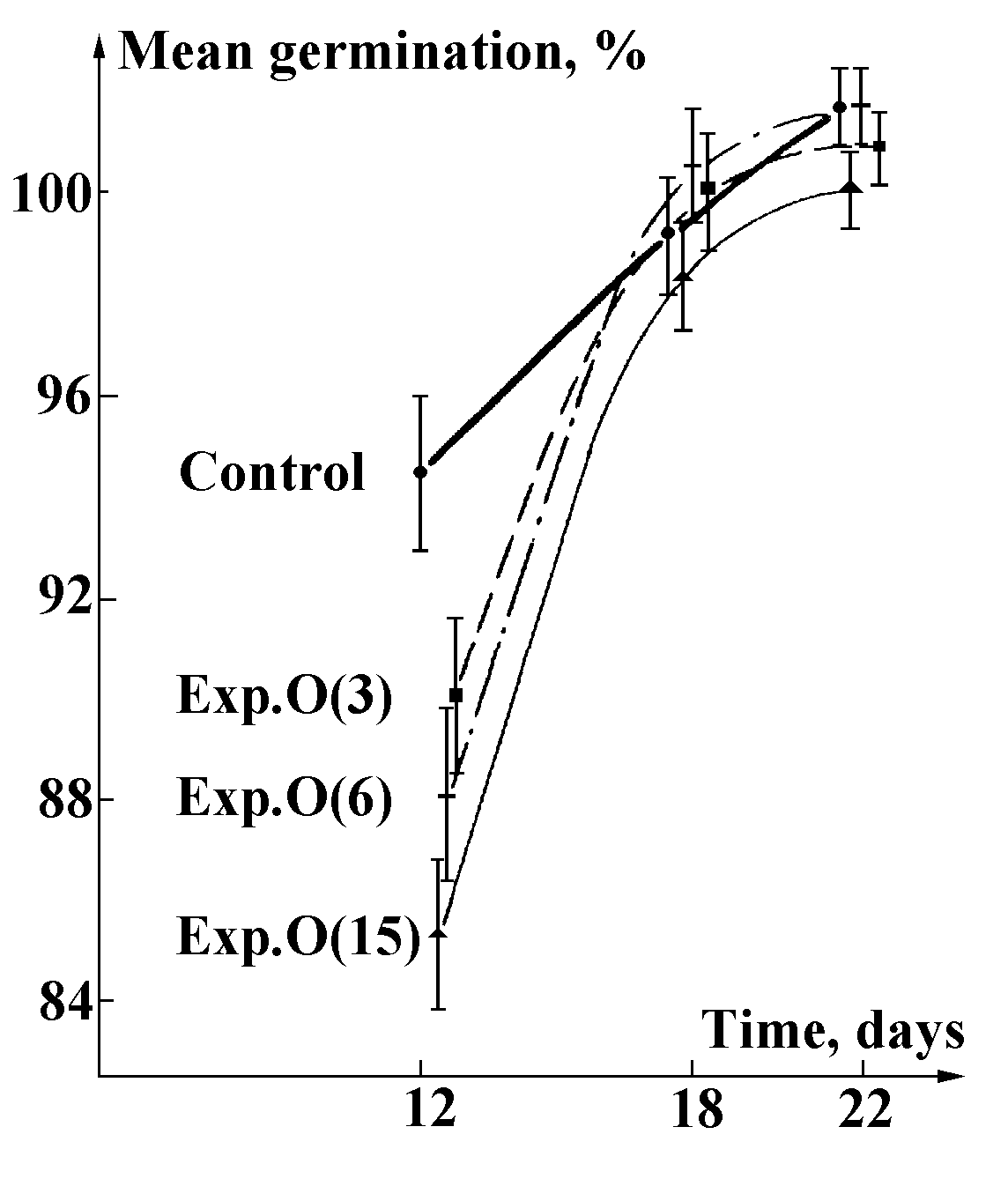
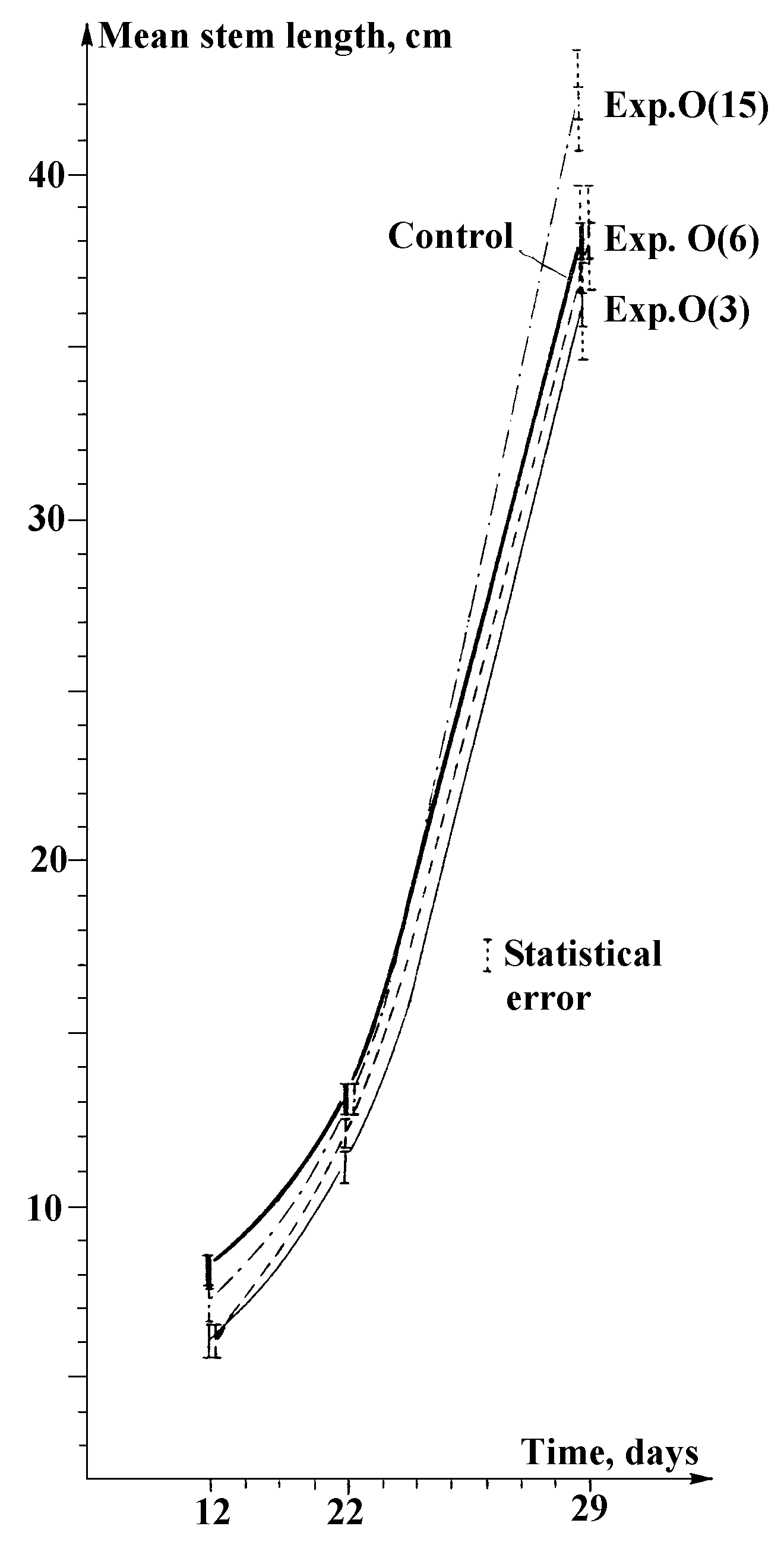
The experiments with germinated pea seeds being subject to liquid nitrogen evaporation process, were continued in a systematic way: “The seeds were subject to action... a day before sowing... dry seeds were subject to action... during two field seasons four experiments were carried out... In each experimental version, combined with reference, three repetitions were accomplished, 175 seeds taking part in each of them... Three versions of action have been tried... irradiating the seeds by the process under study for 15, 6 and 3 minutes. These versions were designated as O(15), O(6) and O(3), respectively... In accord with the number of repetitions three sources of action under study were set in a row. Strictly over each of them (at fixed distance of 65cm for all the experiments) the seeds in paper packages were placed on a cotton fabric stretched over a special framework... The processes of germination, stem growth and development were observed and also a number of... produced seed characteristics were obtained.

Let us sum up the characteristic features of the phenomenon.

As regards germination and plant development, the experimental individuals lag behind the reference ones; however, at a certain stage in some versions of the experiment the lag is replaced by outstripping (Figs.15, 16).

In the most representative class of harvest seeds (making nearly a half of the whole harvest) the weight of 200 experimental seeds... is greater than that of similar reference seeds... The weight distribution of the 200 seeds is a distinct, statistically highly confident response of the biological system used to the action under study.

By the majority of the characteristics considered the mean difference between any of the experimental versions and the reference version is a few times greater than the mean difference between different experiments... In all the characteristics considered one of the common and continual indicators of action is present..., namely, increased variation range: all the experimental plant distributions are characterized by larger dispersions than those of the reference plants...

In experiment organization and interpretation... one should take into account the basic peculiar feature of the phenomenon under study. We are studying the action at a distance of the liquid nitrogen evaporation process on a biological system. However, if a biological system has fixed the action under study, it follows that the same system has fixed, to a certain extent, all the other natural and artificial irreversible physical processes, for which liquid nitrogen evaporation is used as just an efficient laboratory model. That means that the biosystem under consideration is always in the sphere of nearby and remote irreversible processes uncontrolled in the present experiment” (Danchakov and Yeganova 1987, pp.11-81).

It is the true position of the Sun (not the apparent one) that causes biological system reaction (that of Escherichia coli microorganisms): the number of cells able to form colonies on a rigid agared substrate, increases after the action and the cells acquire the ability to actively propagate themselves in essentially unfavorable conditions (Lavrentyev, Gusev et al. 1990).

It should be fixed at once that we are not dealing with a flow in common physical sense. “The additional forces due to the flow are internal with respect to the system” (Kozyrev 1958, p.69). “The necessary existence of two forces resulting from the course of time is of great fundamental importance. This circumstance implies that time can create an angular momentum and internal tensions in a system and their work can change its energy. Hence time can transfer energy and angular momentum but it cannot transfer (linear) momentum” (Kozyrev 1977, p.213).

The angular momentum inherently connected with time introduces inequivalence of the right and the left in the World. Therefore the World “transpierced” by the Kozyrev flow is non-invariant under both temporal and spatial inversions. However, the TP invariance is preserved: “The World with a reversed course of time is equivalent to that reflected in a mirror” (Kozyrev 1963, p.99).

“It turned out that a measurement system can be protected by screens from ... the action of ambient processes. The screens can be made of various rigid substances: metal plates, glass, ceramics, with thickness of 1-2 centimeters. Liquids have a much weaker screening effect: to absorb the course of time by water, a layer several decimeter thick is necessary” (Kozyrev 1977, p.215).

“For instance, for screening the action of acetone evaporation from a piece of cotton wool from about 10cm it is sufficient to take a steel sheet 8mm thick or ten 1.5mm thick glass plates ... while gases cannot be screened at all” (Nasonov 1985a, p.14). Figure 17 shows “torsion balance deflections due to the action of acetone evaporation screened by a cardboard layer of significant thickness, a thin glass plate and a similar plate with an aluminium mirror sprayed. Such a thin layer cannot cause full absorption but it reduced the process action by a factor of two. In other words, in addition to time absorption, there exists time reflection and an aluminium coating is an excellent ... time reflector.

The existence of time reflection was verified by separate experiments. A box with a torsion balance was surrounded by a reliable barrier with a vertical slit. Some processes of liquid evaporation and the thermally neutral process of sugar dissolving in water were accomplished behind the barrier, far from the slit, and caused no effect on the balance. However, a mirror having been placed before the slit and reflecting the process in the proper direction, a repulsion of the balance pointer was observed. Quite naturally the processes attracting the pointer, i.e., absorbing time, are not reflected by a mirror. The experiments showed that the common law of reflection is valid: the angle of incidence equals that of reflection. Therefore a concave mirror should collect and focus the process action and, in particular, observations of celestial objects via time using reflector telescopes are possible” (Kozyrev 1977, p.218). The validity of the reflection law also illustrates the propagation rectilinearity of the Kozyrev flow.

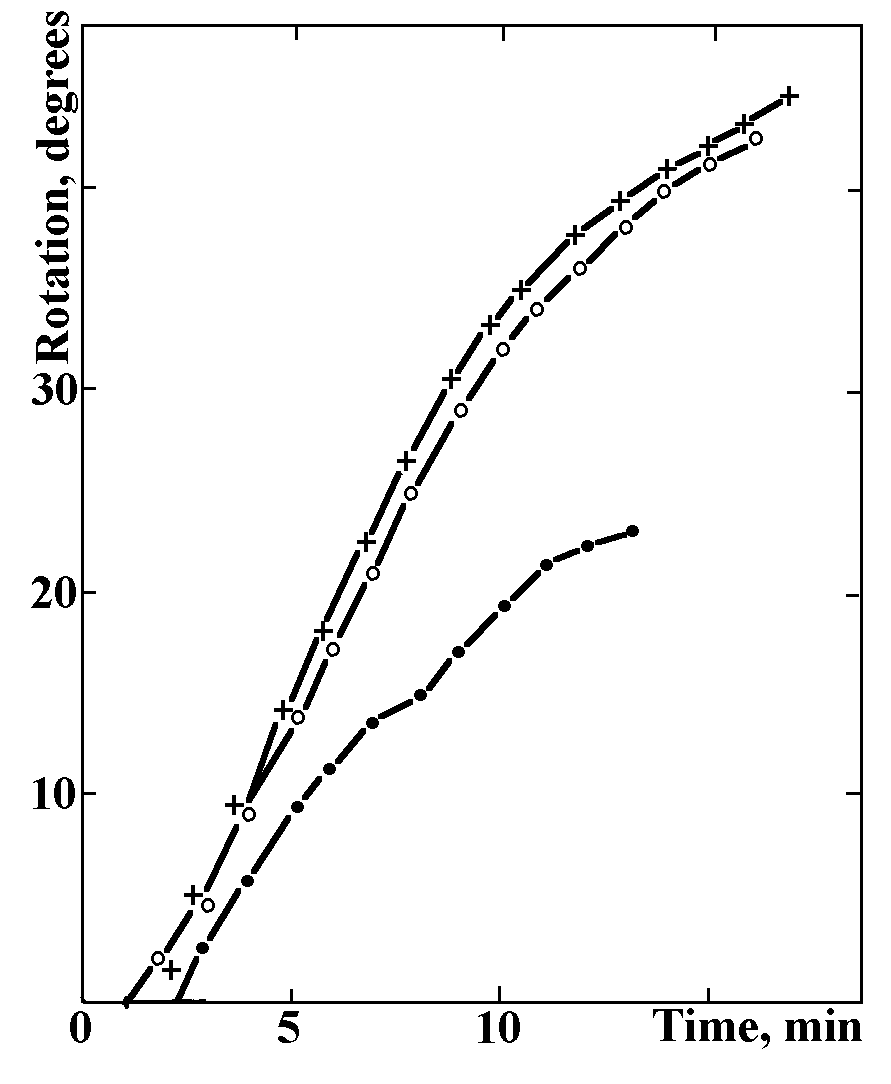
“Our experiments with disks revealed a remarkable phenomenon: a process reflected in a mirror rotates a disk in the direction opposite to that corresponding to a direct action of the same process” (Kozyrev 1977, p.220).

Curiously, an effect detected by a photo-cell, changes its sign on reflection, while that detected by a resistor, remains unchanged (Kozyrev 1977, pp.222, 223).

Experiments with microorganisms (Danchakov 1984, p.108) “confirmed the effect of reversion on reflection, noticed by N.A.Kozyrev in experiments with unanimate matter:... a reflected action stimulates the vital activity of microorganisms, unlike the direct one, carrying suppression”. Also the reflected process of liquid nitrogen evaporation acting on water “unlike the direct action effect, causes an abrupt viscosity increase of about 2.5% during the first fifteen minutes” (Danchakov 1984, p.112).

The Kozyrev flow is reflected by matter but is not refracted, at least in the Earth’s atmosphere, as proved by numerous astronomical observations with the help of the flow, carried out without regard for refraction (Kozyrev 1977; Kozyrev and Nasonov 1978).

“It turned out that in the experiments with vibrating balance (or pendulum) points of support the emerging additional forces... do not disappear when the vibration is stopped but remain in the system for an appreciable time. Assuming that they decrease exponentially..., their relaxation times t₀ were estimated. It turned out that t₀ is independent of the mass of a body but depends on its density r. The following approximate data have been obtained: for lead r=11g/cm³, t₀=14s; for aluminium r=2.7g/cm³, t₀=28s; for wood r=0.5g/cm³, t₀=70s. Thus it is possible that t₀ is proportional to square root of body density. Curiously, additional force preservation in a system after vibration stopping can be observed on a balance in the simplest way. Imagine... a balance with one of the weights hanging from a rubber. Let us remove... that weight... Let us shake the removed weight for some time (about a minute) holding it by the rubber and then return it to the balance. The latter will show gradual weight decrease...” (Kozyrev 1971, p.131). “The largest effects, with maximum preservation times, were observed on porous materials like brick or volcano tuff” (Nasonov 1985a, p.15). Recall that preserved action effect has also been observed by some of the previously described detectors, see Section 2.10 and Fig.10, and also by a photo-cell detector for which “all the features of process action on torsion balances have been observed here as well, including the slow return of the system to its starting position” (Kozyrev 1977, p.222).

The “aftereffect” has also been discovered in a whole series of experiments on the action of different irreversible processes (nitrogen evaporation, substance dissolving in water, water cooling, etc.) on the density of many substances (duraluminium, copper, brass, quartz, glass, air, water, coal, graphite, table salt and others). The effect consisted in continued density and mass variation after action stopping (Lavrentyev et al. 1991).

Along with the effect of action preservation, a curious phenomenon is revealed at the action starting instant as well. “Already in the torsion-balance experiments it was repeatedly noticed that, at optimum experimental conditions, a small deflection of the system readings, directed oppositely to the expected effect, appeared prior to the action. We called this phenomenon “a tail”. It was this sign that we used to select the real effects in the astronomical experiment: noises do not produce such a “tail” (Nasonov 1985b, p.2). See also Fig.3 for a thermocouple detector.

“... A body placed for a certain time near a process and then brought to a torsion balance, produced the same effect on them as the process itself. Memorizing the action of processes is a feature of different substances, except aluminium” (Kozyrev 1977, p.217). Also for a photo-cell “the action curve of a body which had memorized a process, turned out to be similar in details to that of torsion balance deflections. Likewise, aluminium showed no memory. The largest memorizing effect for processes of both signs has been shown by sugar...” (Kozyrev 1977, p.222). “Thus, it turned out that water with decreased viscosity after being subject to the action of a process, exerts a distant action on water having not been under such an action, causing its viscosity to decrease” (Danchakov 1984, pp.111-112).

“In the vibration experiments on a balance the weight reduction DQ occurs stepwise, beginning with a certain vibration power. As vibration frequency is further increased, the weight reduction DQ at first remains the same and then again grows stepwise by the same value. Thus it has been observed that, apart from the basic step DQ, good harmonic oscillations make it possible to see a series of quantized values: DQ/2, DQ, 2DQ, 3DQ,..., corresponding to continuous vibration frequency increase. The observations show that vibration energies for the beginning of each stage form apparently the same series... It seems that a balance with an excited degree of freedom behaves like that without oscillation, while additional vibration energy causes an equal step DQ. So far a realistic explanation of this phenomenon has not been found. The origin of a half quantum number remains quite unclear. Similar quantum effects have been observed with pendulums. Afterwards it turned out that effect quantization takes place in almost all the experiments” (Kozyrev 1971, p.126).

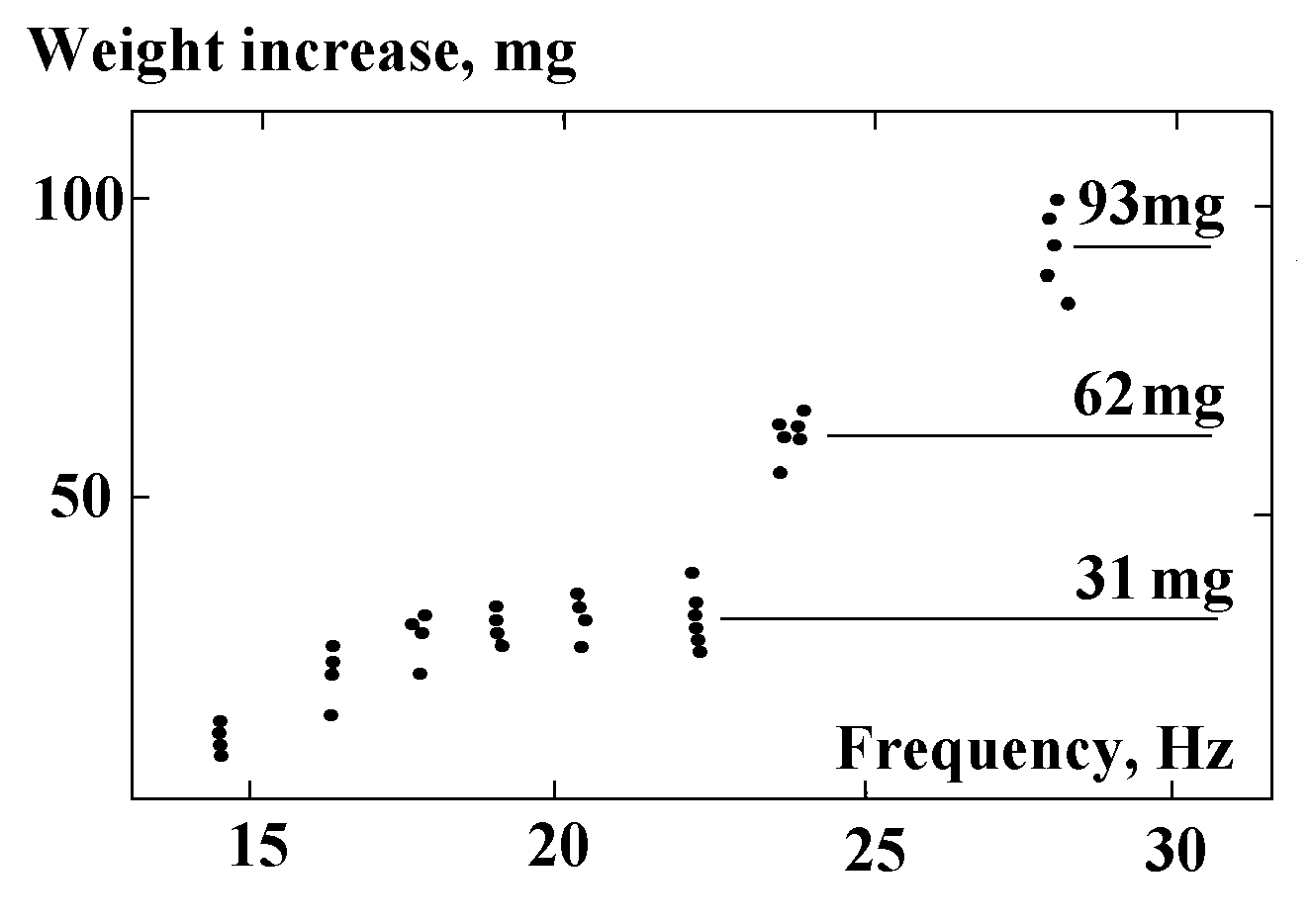
“... We succeeded in obtaining fivefold and even tenfold effects. As a result, the determination accuracy of a single effect could be increased by a certain factor. Figure 18 presents a typical dependence of weight increase on vibration frequency. The measurements have been carried out by Yu.I.Kulakov and the author at Pulkovo on a second-class beam balance... The graph shows the weighing results for a weight of 620g renormalized to that of 1kg. The beam support vibration amplitude was about 0.3mm... The graph shows quite distinctly three stages of weight increase” (Kozyrev 1963, p.108).

Figure 12 shows the results of weight measurements at two vibration frequencies causing the first- and second-stage effects. For pendulums the weight change quantization effect was observed not only after vibrational excitation but also due to excitation by an electric current, heating or cooling. Therewith the electric current and heating created half the deflection stage observed by vibration (Kozyrev 1971, p.127). A torsion balance “leaves its normal, zero position with a certain difficulty. After that comparatively rapidly it passes to another stable position and keeps it until an intense action makes it pass to yet another stable position; although these stable states are not very clearly expressed, the following series of values may still be selected:

0, j /2, j , 2j , ….

For a sensitive torsion balance j=20°” (Kozyrev 1974). Multiple effect stages in the operation of a thermocouple detector are clearly seen in Fig.8.

3.8. Density

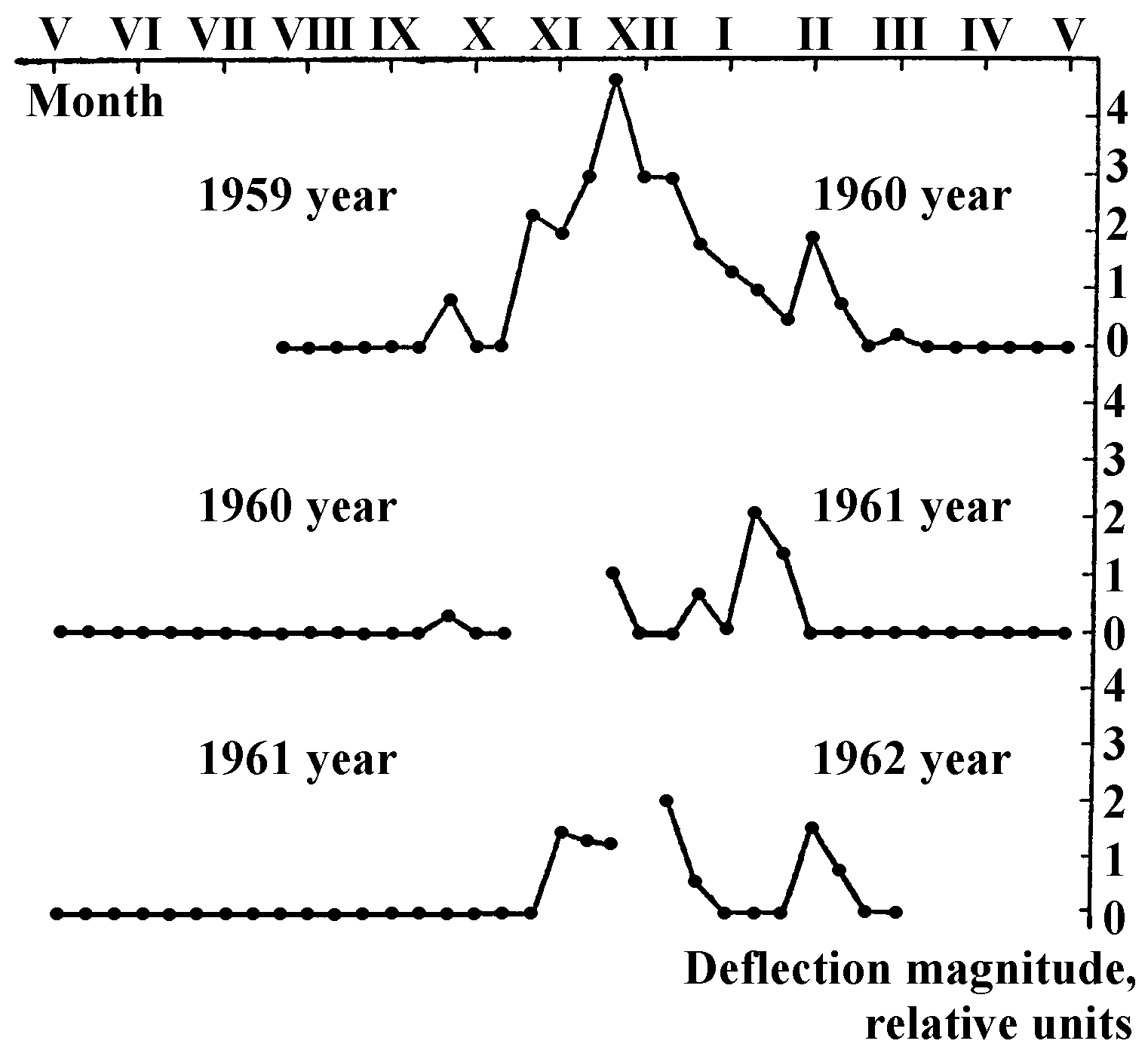
The experiments with weight vibration on a balance make it possible to introduce a coefficient equal to “the ratio of vibration acceleration needed to obtain the first stage, to gravity acceleration. For the data of Fig.18 one obtains the value of about 20-30%. The observations have shown that, despite a strict observation of the same experimental conditions, this coefficient varies over a vast range, from a few to nearly hundred per cent. Apparently it varies due to some outward circumstances, occurring outside the laboratory. Often sudden and quite irregular changes of that coefficient happened, taking place during a few minutes. There is an impression that these changes catch the evidence on some processes occurring outside the laboratory and maybe outside the Earth... Therefore the experiment with a pendulum does not always yield deflections.

Figure 19 shows the results of three years of observations over a pendulum kept all the time in the same conditions. The vertical scale is formed according to the following gradations: 0.5 — a hint of the effect; 1 — obtained with difficulty, at a very strong resonance; 2 — at medium-range resonance, 3 — at small resonance, 4 — nearly without a resonance. The figure plots average data for decades. A remarkable general law of the effect emerging conditions is obtained: ... it is observed most easily in late autumn and winter... in summer the effect on a pendulum was never observed... At the first sight it could seem that the difference in the experiment reproduction conditions, provided that equal laboratory conditions have been kept, is unplausible and that it casts a shadow on the reality of the results presented. However,... from the most general theoretical standpoint we ought to expect that some properties of time would be able to vary. It is natural to assume that the observed strength of causal relations is different due to a variable property of time which could be called its intensity. This property of time is similar to light intensity which characterizes light apart from the constant propagation velocity. Variations of the intensity of time should be caused by some physical processes, so far unknown” (Kozyrev 1963, pp.111-112).

“...Sometimes the experiment bring an easy success, while sometimes under exactly the same conditions they turn out to be fruitless. These difficulties have been noticed in the old experiments on southern deflection of falling bodies as well... There exists a variable property which could be called density, or intensity of time... Apparently many circumstances exist which affect the density of time in the space surrounding us. In late autumn and in the first half of winter all the experiments are successful. In summer the same experiments are hard... The experiments at high latitudes are much easier to realize than in the South...

It is sufficient to take a simplest process to try to change the density of time. For instance, one can raise and lower a weight by any types of motor, or vary the tension of a tight rubber. A bipolar system is obtained: there is a source of energy and its discharge, i.e., a cause-and-effect dipole. Using a stiff transmission, one can move the poles apart from each other to a considerable distance. Let us draw one of the poles near a long pendulum with a vibrating suspension point. The vibrations should be adjusted in such a way that, instead of a full southern deflection effect, just a tendency of it emerge. It turned out that this tendency markedly increases and can even pass to the full effect when the pole of the dipole where the energy is absorbed, is brought near the body of the pendulum or its suspension point. If the other pole (the motor) is brought near, the observation of southern deflection always becomes more difficult. When the poles were placed close to each other, their effect on the pendulum practically disappeared. When a weight of 10kg, suspended from a block, was raised and lowered, its influence was felt from distances of 2-3 meters from the pendulum. Even a thick laboratory wall was unable to screen this effect. There occurs time rarefaction near the motor and its compression near the receiver” (Kozyrev 1971, pp.128-129).

Figure 12 illustrates the effect of time flow density decrease due to a solar eclipse. The effect consisted in diminished additional weight increasing forces on a beam balance in the vibrational regime. Also “for a number of years, in February and March, in Pulkovo we observed an abrupt jump of vibrational balance readings coinciding with the true sunset, without regard for refraction, up to a minute” (Kozyrev 1977, p.216).

“Geophysical factors should lead to seasonal and diurnal changes of matter states. Instrument drift, indicating the diurnal changes, usually stops near midnight and then changes its direction. In the seasonal course, the density of time decreases in spring and summer and increases in autumn and winter. Most probably it is connected with the life of plants which absorb time in their active period and return it when fading. These circumstances have been observed by many authors in a large variety of investigations. Of interest is, for instance, the information from A.Shapovalov (1973), a biologist from Dnepropetrovsk, who observed photo-multiplier dark current for three years. The dark current increased by two orders of magnitude from the end of May till autumn (Fig.20), pointing out that the obstacles for electron emission are being weakened...” (Kozyrev 1982, p.70).

“It should be noted that all the balances exhibit one more effect of interest, so far having no clear explanation. Vibration energy necessary for exciting a step, depends on the azimuth of the balance. The energy is the smallest when the weight suspended from a rubber is to the South from the balance upright and the largest when it is to the North” (Kozyrev 1971, pp.126-127).

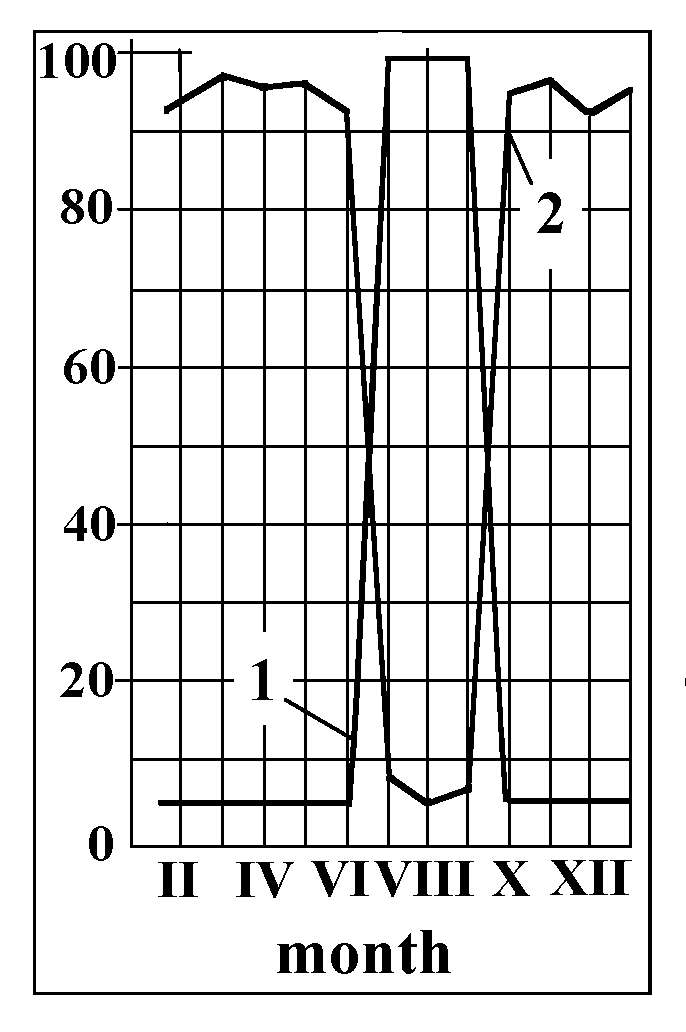
By N.A.Kozyrev, time, like space, possesses both geometric and physical properties (for space those are the metric, on the one hand, and the force fields, on the other); the geometric property of time is duration, while physically the course of time is similar to field propagation and the density of time to field intensity.

“Time density is a scalar quantity, just the one observed in the above experiments. Time density decreases with increasing separation from the process creating it. Therefore a vector property, corresponding to density gradient and tractable as time obtaining, should also be observed” (Kozyrev 1977, p.216). Essentially the density of time is the characteristic whose gradient is the Kozyrev flow. I would like to present a set of synonimic descriptions from N.A.Kozyrev’s works, used to designate processes and phenomena connected with the time flow: time density decrease = time absorption from the ambient space = torsion balance point attraction = heat releasing process = loss of organization by matter = entropy production. The term “time density increase” creates a similar chain of opposite descriptions. However, an irreversible process is not a necessary condition for Kozyrev flow detection. Indeed, irreversible processes create the flow. However, the Kozyrev flow and the corresponding interactions can be observed in equilibrium situations (from the viewpoint of energy or matter conservation). Among the experimental examples of Section 2 those are the experiments with additional forces emerging because a body takes part in two types of motions (rotation and vibration, rotation with the Earth and falling to the Earth and others).

If one adheres to the views of the substantial nature of the time flow, then one may speak of two velocities connected with that flow. One of them is the flow velocity with respect to fixed points of matter and space. The other one is that of excitation (wave, signal) propagation in the substance itself.

By N.A.Kozyrev, the first of these velocities is apparently the universal constant c₂, “the cause-effect conversion velocity” (Kozyrev 1963, p.98). “The numerical value of c₂ might be estimated from dimensional considerations... Using the Planck constant , one easily makes sure that

km/s,

where e is an elementary particle charge and a is a dimensionless factor...” (Kozyrev 1963, p.102). Thus the ratio of c₂ to the velocity of light c₁ is proportional to Sommerfeld’s fine structure constant: c₂/c₁ » 1/137 (see more details in L.S.Shikhobalov’s chapter in the present book on the uncertainty relation derivation).

N.A.Kozyrev believed that the signal propagation velocity c₃ in the time flow is infinite; the argument was that time does not carry momentum and “does not propagate, emerging at once in the whole Universe. Therefore organization and information can be transferred by time immediately to any distance... The possibility of instantaneous signal propagation is not at variance with the theory of relativity since such a transmission is not accompanied by a material motion. Therefore there is a possibility in principle to fix the true position of a star along with its apparent position” (Kozyrev 1978a, pp.169-170). Measuring the angular distance between the true and apparent star positions, provided that its proper motion is known, it is possible to determine the parallax of a star strictly trigonometrically; this has been accomplished in a few series of astronomical observations (see Table 1 in the present review). The parallax values, calculated on the basis of time flow detection by resistor probes for about two tens of astronomical objects up to 2ґґ-3ґґ (i.e., of the order of slit width), coincided with the known parallax values from Genkins’ catalogue (Kozyrev 1978).

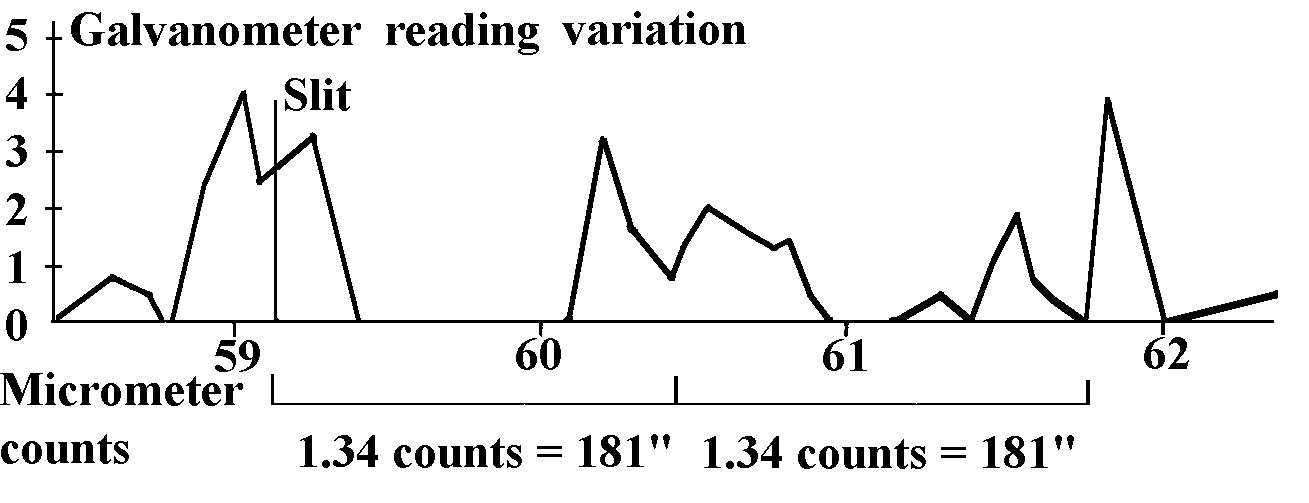
It turned out in the process of astronomical observations that a probe, fixing the Kozyrev flow from a star, actually fixes: “(i) the star position at the present moment, (ii) the star position in the past, coinciding with its visible image up to refraction, and (iii) the future position to be occupied by the star at the instant when a light signal emitted now from the Earth, would reach it” (Kozyrev and Nasonov 1980, p.76). Figure 21 shows the “temporal activity” profile of the Andromeda nebula. “Along the ordinate axis... the galvanometer reading changes are plotted in terms of its scale divisions for different micrometer counts plotted along the abscissa axis. It is remarkable that the three predicted profiles, corresponding to the past, present and future states of the nebula, are distinctly observed. Certainly the difference between the profiles is due to measurement errors since no significant changes could occur in the state of the nebula during four million years separating the two extreme images. What is real, is the activity decrease near the center of the nebula repeated in all the three images” (Kozyrev and Nasonov 1980, p.92). N.A.Kozyrev interpreted the detection of three “temporal” images of the same astronomical object as the motion of a “temporal signal” with the velocities equal to c₃ = , +c₁ and -c₁ (c₁ is the velocity of light), and as a “proof of the reality of the four-dimensional Minkowski space” (Kozyrev 1980). See also the modern experimental work by Lavrentyev with co-authors (Lavrentyev, Gusev et al. 1990). At any rate, the above astronomical observations provide an empirical ground for believing that and for discussing the possibility of “determination by the future”.

Maybe, beginning with the first pages of the present review, one and the same question arises in the reader’s mind. Let a certain substantial flow exist in the Universe; let that flow feed stars with energy saving the Universe from the bugaboo of thermal death; let the flow substance be emitted and absorbed by matter thus exerting influence on different kinds of detectors; let that flow even be a necessary component of living matter organization on the Earth. But what has that flow to do with time? It should be noted that N.A.Kozyrev never spoke directly of a substantial flow: as it has been noted, it is just one of the possible interpretations of Kozyrev’s “time flow”. The idea of a “substantial time” is implicitly contained in Kozyrev’s conception (the corresponding argument can be found in the first section of the present review). Actually N.A.Kozyrev deals with the causal relation concept. A substantial interpretation is obtained if one replaces in Kozyrev’s considerations the term “existence of a causal relation” by the term “existence of a pre-particle flow”. Thus a logical chain emerges: a substantial flow — the causality principle — the idea of time, since just the Kozyrev flow is responsible for “cause-effect transformation”, for cause-effect asymmetry due to unidirectionality of the flow, for spatial and temporal separation of causes and effects and for the finite velocity c₂ of the cause-effect transformation. Also implicitly Kozyrev’s conception contains the statement that the directionality of the temporal order of events originates from the physical causality principle, thus “locking” the idea of a substantial flow to the concept of time flow. A more detailed discussion of the relation between causality and Kozyrev’s conception of time is contained in the papers by N.A.Kozyrev (1958), I.A.Yeganova (1984), M.L.Arushanov and S.M.Karatayev (1989) (see also references in S.M.Karatayev’s chapters in the present book).

There is a viewpoint (Levich 1989, part 1 of this book) which has actually created the substantial interpretation of N.A.Kozyrev’s conception discussed in the present review. By that viewpoint, the existence of a substantial flow is an ontologically necessary condition for the idea of time to emerge in natural science. The metabolic time and metabolic motion construction allows one to describe flow propagation without momentum transfer, the existence of corrections proportional to the ratio u/c₂ in the equations of motion (where u is the motion velocity of a body and c₂ is the metabolic flow velocity) and some other features of the Kozyrev flow.

The Kozyrev flow creates the idea of a new universal interaction of material bodies. This interaction can be illustrated on the physical peculiarities of binary star components (Kozyrev 1968): in binaries a satellite is an unusual star, since the long binary existence results in its likelihood with the main star by a number of physical parameters (brightness, spectral type, radius). At such large separations the usual type of influence (via force fields) is excluded. Kozyrev’s interaction might be the cause of some terrestrial and lunar tectonic processes (Kozyrev 1971), some Earth-Sun relations, stellar and planetary influence on some processes happening on the Earth, and some living organisms’ interrelations (Kozyrev 1971). Kozyrev’s interaction is not invariant under spatial and temporal parity changes. The “meta-interaction” conception, initiated by N.A.Kozyrev’s ideas, is presented in detail in I.A.Yeganova’s paper (1984).

In my view, the following three conditions are necessary for the development of N.A.Kozyrev’s conception:

A constructive formulation of the problem is not the question, whether or not the substantial flow exists, but in searching a solution on the way proposed by N.A.Kozyrev: how could one operationally exhibit this flow, i.e., the methods of changing reproducible flow characteristic, different from the basic one (i.e., our ordinary time flow), should be improved. Recalling analogies from history of physics, one could suggest that we are now in a situation like that of Galvani, observing a frog paw tremble due to hypothetical electric charges, while we need Faraday’s frame, able to generate electric current and reveal the action of invisible magnetic fields...

REFERENCES