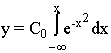Among numerous searches of constructive solutions concerning the problem of time structure of biological systems, the most outstanding is Gaston Backman's (1883-1964) conception of organic time. Developing his general growth theory of living beings, he has also been engaged with the problem of time. For this purpose extensive investigations of the growth processes of people, plants, lower and higher animals have been made. Backman's first work in this field has been published in the Proceedings of University of Latvia (Backman 1925), where according to the invitation he was working in the Faculty of Medicine (1920-1925), having organized there a Department of Anatomy and Anatomical museum. The results of his long-term research when he was a Chairman of Institute of Anatomy of Lund's University in Sweden, has been summarized in his book "Growth and Organic Time" (Backman 1943). The following phrase can be found in the afterword of this book: "Growth is the basis of life and is a sure expression of the inner source of life (...). The possibility to foresee the events of life's run is based on the knowledge of the fact that the organisms have their "own time", what I call organic time" (Backman 1943, pp. 177-178).

This theoretico-methodological approach has both inductive and deductive basis. Theoretical postulates have been concretized in the form of mathematical models. Vast experimental data about the growth of organisms has been used to test the adequateness of organisms taken from several classes of multi-cells. Having analyzed the known growth formulas of organisms, G. Backman distinguishes their insufficient adequacy. So, the symmetrical т -like curve, with which commonly the growth of organisms has been approximated, does not show the characteristic peculiarities of their growth. This peculiarity is the following: the period of slowing down the growth rate is usually longer than the period of its increase. Therefore half of the organism's ultimate length is reached after the growth maximum, but before the middle of its individual life duration. This phenomenon was explained with the fact that biological development has a logarithmic character. In this case, the time of biological phenomena is understood as a logarithmic function of the physical time. The growth curve of an organism, being based on such organic time, is symmetrical.

G. Backman, after T. Robertson, classified 3 growth cycles of multi-cell organisms: ovular, primordial (embrional) and infantile (basic growth); for mammals - a cycle of sexual maturity has been added, which covers with the stages of the basic growth. The second cycle doesn't end with birth or seed growth, but continues some more time, covers the already begun third cycle. The monocell organisms have only one cycle of growth - the great ovular period. Some more developed volvoxes (colonial forms) in addition to this cycle, have the second - the great embrional (primordial) period. In the process of further evolution, the third cycle appears, which begins to take a greater period in onthogenesis (for plants 75-85%, for animals 90-95%, for man about 99%). Each cycle is characterized by its own rate of organic time and therefore, it must be detected separately. The comparison of organic time of different species of organisms (or populations) and the stages of their growth, using the formulas by G. Backman, must also be carried out according to the growth cycles.

As the initial information for obtaining G. Backman's function consists of the quantitative values of the organism's growth process (growth in length, growth in mass, etc.), he substantiates the sufficiency of such information with the fact that the growth process is the basis of life, expresses its inner nature and is closely related to other main biological processes and phenomena of the organism.

The conceptual basis of Backman's function of growth, is the postulate that the logarithm of growth rate is negatively proportional to the square of time's logarithm

log H = k2 log2T. (1)

Constant k2 is always negative. But it doesn't mean that the rate of growth is always lowers. In the interval 0<T<1, the rate will become greater, as the logarithm is negative.

Backman introduced indicators "normal time" (that is the moment of time, when the growth rate is the greatest), which is used as a unit of time, and "normal rate" (the growth rate, in the moment, when it is expressed most of all), which is accepted as a unit of the rate. As during the greatest growth, genetic program, specific for species of the given individual, is being realized, the unit of time detected in such a way can be compared among organisms of different species.

For the detection of the growth curve (y), according to its rate, Backman used the integral function

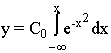, (2)

where C0- constant of the proportionality of quantitative growth values according to standard integral;

x - measure of organic time, to be detected by the formula

(3)

Eq. 3 is the function of organic time. The constant C1 is the scalar of organic time.

The constant C2 expresses the logarithmic value of the physical measure, with which the time necessary to reach half of the whole size t0.5 is measured, taken proportionally to the scalar value C1.

The relationship between C2 and C1 is a logarithmic measure of the usage of the scale of physical time. With the transition from one scale of physical time to another, changes only value C2, which is growing according to the lowering of the unit of physical time.

Backman mentioned the principal similarity of his Eq. 3 to the formula of the time of a dynamic event (Eq. 4) derived by astrophysicist E. Milne (1937). Milne's formula is as follows:

, (4)

t0- the value of t at the initial moment;

t - age of the Universe.

G. Backman believed that values x2 = 0/2; 1/2; 2/2; ...; n/2 have an especially important biological significance. The difference of these values is a constant

. (5)

He named this difference the quantum of life and stated that x2 of an organism at a given instant reflects the number of the already gone through and forth coming quanta of life. On the basis of this concept Backman derived a formula of detecting the time of the most greatly expressed potencies of life ("strength of life") t_v, the transition time from quick to slowed down aging ta and the general life duration td.

The puberty is reached when . Moving away from this point of time, the intensity of the appearance of quanta of life diminishes, as they correspond to smaller intervals of organic time. When , the life of an organism commonly ends.

With the increase of the age of the organism, to every further unit of physical time there corresponds smaller organic time - the acceleration of physical (kinematic) time is taking place. Backman defined the absolute acceleration of physical time Dt as the amount t, corresponding to the constant interval of organic time of an organism Dx in the different age.

As depends on C1, this value is different not only for different organisms, but also for the organs of an organism. To overcome this difficulty, Backman introduced the concept of relative acceleration of physical time as the relationship of the index of absolute acceleration of every year of life tn between the absolute acceleration of the given year of life tp. The relative acceleration of physical time does not depend on the type of growth and is the same for different organs and parts of organs of an organism. It is like a measure of absolute age of organism, being measured according to "biological clocks". In relation to the psychological perception of the acceleration of the physical time, Backman imagined the passed part of life as a unit, where, for example, the eighth year of this unit is 1/8, but the twentieth - 1/20. Or in general: one year - this is 1/tn and a year tp - 1/tp from this unit of already gone through life.

Backman's function has been discussed in literature for several times. I. Weck (1953) has positively estimated the possibility of its usage in forest - biological investigations. H. Thomasius (1965) subjected Backman's function to critical analysis. On the basis of G. Backman's formulas, he made a nomogram, with a help of which on the basis of initial information, it is possible to detect quickly the necessary constancies (C0, C1 and C2) and "organic time" x. Having analyzed a great amount of material, H.Thomasius came to the conclusion that Backman's function can be used to approximate empirical data of tree mass growth, but this function is of little use for the exposure of growth in height and diameter. He noted, that Backman had not given a unique way for detecting the lengths of the second (primordial) cycle of tree growth with indicated strict biological criteria of its borders: there lack a sufficient biological interpretation of the function's constants and measurements; besides that, this function for every cycle of life has different constants, which makes its application difficult.

The results of our research with tree species attest the conclusion of Thomasius according to initial information. Better results were achieved using quantitative values of the growth in size. The inclusion of the conception of time itself x in the mathematical model of prognosis of wood growth, essentially increased the informativity of the model (Maurins 1980). Interesting results were obtained in the research of the application of Backman's function for the prognosis of potential anthropotolerance of trees. In Riga Seaside sample plots were selected, relatively homogeneous from the point of view of anthropogenous influence, and from the Pinus sylvestris trees growing there a group of obviously unresistant (evidently degraded, withering), and a group of antropotolerant (good state) was distinguished. For further calculations data about the current wood growth of these tree groupings for the retrospective period of 80 years have been used. Backman's function values for these two groups, essentially differed also before the period of negative human impact. The trees, which appeared to be anthropotolerant (resistant), differed with the great curve (that is with more greater rate) of the time in the early periods of onthogenesis. These results testified that Backman's function can be used in the prediction of tree anthropotolerance. However, for the development of a concrete methodololgy for the usage of this principle in the selection work, further research is necessary.

We have also used Backman's function for the unified formalization of tree species age (Maurins 1982). The concept of the age of plant species has entered biology due to the works of N. P. Krenke (1940). Nevertheless, the distinguished age characteristics are specific for species; which is one of the reasons for the wide usage of this approach. It is actually the task of unified age formalization. One of the possibilities to solve this task has been offered by A. A. Uranov (1975). He divides plant onthogenesis into 10 age states: sprouts (shoots), juvenile, immature, virginal (young vegetative), young (early-) generative, middle-aged (mature) generative, old (late-) generative, subsenile (old vegetative), senile and dying off ("almost corpse") plants. Equaling the amount of energy to one, accepted by the plant during all the time of onthogenesis, but the age of the individual - to the part of the energy, which is assimilated in the middle of the given age state, he has derived the age state formula

, (6)

where m - age of an individual;

t - stage of age state in forces (0-10).

It's interesting to note that A. A. Uranov's hypothesis about prolonging the middle time of individual in each further state of age, beginning from sprouts up to mature generative individuals, correspond to G. Backman's law of the acceleration of physical time during the onthogenesis. The data comparison of age states and age according to A. A. Uranov with the corresponding intervals of the organic time, calculated by us according to Backman's function for Pinus sylvestris (Table 1) is of interest. As the biological time (according to Backman's function) in the beginning of onthogenesis has a negative value, its intervals (quanta of life) in the last column of the table for p, j, im, v, g1 are also negative. The quantitative values of the intervals of time of individuals are approximated to . Each state of age, beginning from virginal, concurs with one "quantum of life". More early age states involve several such "quanta". Such difference of these two age states in relation to the following, can be explained by their complex character. Evidently, immature plants are going through two age states, but juvenile - three. Similar results have also been obtained as regards the stages of organogenesis, distinguished by F.M.Kuperman (1952). Also in this case, the first two stages appeared to be complex, involving several "quanta of life". Therefore, Backman's function can serve as an estimate of empirically detected qualitatively different intervals of onthogenesis (periods, stages, age states, etc.) and more general, deductive positions.

The formalization of plants age with the aid of Backman's function has been used for forecasting of tree species quick fruiting (Maurins 1987 a). We used one-year seedling of common apricots planted in the Botanical garden of the University of Latvia (Riga) as sample objects. The date that each seedling started to grow was recorded and their lengths were measured every 5 to 7 days. For the majority of seedlings two waves of growth were clearly observed. For other seedlings, these two waves overlapped to some extent during the vegetation period, although the trajectory of the whole growth formed a two-top curve. Therefore, there were no difficulties in separating the curves of the first and the second peaks. For the first and the second peaks Backman's function was calculated separately, as the function's constants differed. However, a general low has been revealed: more accelerated seedlings (those with greater organic time rate) as observed by both peaks afterwards exhibited quicker fruiting. They be fruits at the age of four, while the greater part of seedlings only at the age seven or eight. The potentially quick fruiting of one-year seedlings could be seen by clear indications of comparatively greater age, according to H.P.Krenke (1940): greater number of leaves per unit length of the seedling, the quicker transition in the form of leaves (from seedling to mature), the appearance of side sprouts.

As a result, the trend of age autotemporality, described by Backman's function already in the early stages of onthogenesis, reflects the biological disposition of the individual. This aspect not only contributes to the development of methodology of organism development forecasting in different conditions, but also can be used as a constructive tool for the propensity interpretation of probability, determined by an organism's genotype and to what extent - by the changes of environment. G.Backman himself, according to the formal concepts and analysis of the results of experimental research came to the conclusion that "the environmental conditions do not influence C1 and thus C1 is likely to be determined by genetic factors. At the same time it is clear that the numeral value of C2 can be easily modified by changing the environmental conditions" (Backman 1943, p. 169). We tried to test Backman's conclusions on the objects of our research. The individual differences of values of constant C2 always appeared to be essentially greater than those of constants C1 throughout the population. The growth analysis of Pinus sylvestris whose plantation site has been 27 years ago subject to melioration, showed that after melioration the character of the tree's organic time changed drastically, mainly due to constant C2 variation. Actually the values of constant C1 varied slightly as well; it may result from some changes in genotype (e.g. a transition of some related genes into the additive state) due to such a strong "shock" like rapid improvement of soil aeration after drainage.

The relationship of quantitative values of the constants C2 and C1, as mentioned before, has a fundamental significance in the determination of onthogenesis. G.Backman used this relationship to derive the formula of potential length of an organism's life

. (7)

The numerator of the second term of Eq. 7 is the theoretical life duration in terms of organic time (that is x==1.22474). We tested Eq. 7 in dendroecological studies of several autohtone and introduced tree species (Maurins 1979). In all cases, quite reliable results were obtained. For example, the practice of foreign perennial plant cultivating showed that in the conditions of introduction, their life duration is much shorter than in their native area. Using G.D. Jaroslavtsev's data of stem analysis of two specimens of Sequoiadendron giganteum (so called mammoth-tree) introduced in the Crimea died for different reasons at the age of about 70 and 100 years, we calculated their potential life duration using Eq. 8. The calculations showed that natural death would take place at the age of 152 for the first tree, and at the age of 145 for another one. According to the dendrochronological data of A. Douglass (1941), who has made the same calculations for two trees of this species in the native area (California), the potential life duration of one tree, appeared to be 2463 years while that of the other 3238 years.

We used Backman's function to detect the temporal (functional) harmony, as an indicator of adaptation of trees as well (Maurins 1987b). Conceptually, such approach is based on the idea about adaptation as organism's harmony (Jablokov 1981). E. M. Soroko (1984) has written that harmony is a stable unity of diversity, taking place near appropriate knot points (invariants) of state (distribution of parts) of the system

, (8)

where H-relative system's entropy (the measure of the distribution of the parts of the whole); S = 0, 1, 2, 3, ...; when S = 1 the known "golden section" takes place.

"The transition from one system's organization level, regimen of functioning or the amount of its inner-structural diversity, to the other one means the change of S-algorithms, corresponding to its separate stable conditions" (Soroko 1984, p. 205). Necessarily, such a transition crosses the zone of disharmony most obviously manifested when S = 1/2, 3/2, 5/2,..., while integer values of S-algorithm correspond to the harmonically most stable conditions.

In complicated systems with interiorly structured relative enthropy, determined by the distribution of components p₁, p2, ... , p_n; we get

, (9)

where n is the number of states (events, parts in the whole etc.).

To approximate temporal (functional) harmony we used physical (calendar) time intervals corresponding to “quanta of life” as a structural unit of organic time as values of pi. Temporal harmony was calculated for autohtone (native) and introduced species, individually differing in their state. Table 2 contains data for local (Picea abies and Pinus sylvestris) and introduced species (Abies concolor, Larix ledebourii, Picea sitchensis, Pinus banksiana, P. strobus, Pseudotsuga menziesii and Thuja plicata, being cultivated in Latvia and Kaliningrad region). The reason of local species Pinus sylvestris and Picea abies degradation is due to a long-termed influence of adverse anthropogenic factors. It is clear from Table 2 that the closer is the quantitative value S to an integer, the better is the condition of a tree and vice versa. The question of biological interpretation of changing S-algorithms (S = 1,2,3 etc.), corresponding to certain stable conditions during the process of plant adaptation, is of interest. To get the more correct answer to this question, further research is necessary.

G. Backman's concept of organic time in its theoretical substantiation, methodological and methodical elaboration has a fundamental place in biotemporology. It is necessary to note that he understood temporal relationship in animate nature in close relationship with spatial aspects. "Thus", he wrote, "I consider that living organisms develop in a logarithmical world, where the spatial and temporal values have a logarithmical scale (Backman 1943, p. 43). The problem of spatial-temporal states and relationships in animate nature is the subject of a separate paper.

To G. Backman's temporal conclusions comes also a well-known mathematician-systemist B. C. Fleisman, working on the problem of adaptation of regenerative systems in the context of developing a theory of potential effectiveness of complicated systems shares G. Backman's temporal conclusions. He has written (1986), that his results correspond to "Backman's law". "The problem is not to suggest the best mathematical approximation of empirical data", but that "logarithmical curves of growth result from optimization laws of systemology and the stability of biorhytms is regarded as their high liability, maintained by minimal order of growth of their elements." (Fleischmann 1986, p. 95).