BIOLOGICAL TIME, ITS ORGANIZATION, HIERARCHY AND PRESENTATION BY COMPLEX VALUES
G. E. Mikhailovsky
1. Biological time organization
Speaking of biological time as well as biological space we shall always have in our mind the time (or space) taken (filled, organized, interpreted, etc.) by the biological system (cell, organism, population, ecosystem, biosphere). In this sense biological time does not oppose physical one and only organizes it. However, this kind of organization provides biological time and space with definite specific properties.
In architecture there exists the idea of "space organization" and it means filling of certain empty volume by a system of walls, overlaps, stairs, aisles, doors, etc. All these architectural elements play the role of barriers and canals turning the real shortest way between two points out of a straight line into a broken one or, in general case, into a fractal or a curve. The example of an organized, in this sense, space can be a block of houses built in a town where the actual way between the neighbouring flats from different houses is far longer than a few meters which separate the flats from one another with physical space.
In this sense the space of biological systems is very well organized, which is followed from the level of biomembranes and up to the most complicated organization of natural landscapes, and the biosphere as a whole. In such an organization the specificity of the biological space is developed. V.Vernadsky called it "non-Euclidicity" (Vernadsky 1924; 1929). In fact, the straight line does not represent the actual distance between the objects in neither endoplasmatic reticulum nor the blood system, nor the tropical forest, nor the coral reef.
And what about time?
Is it possible to say about its organization? And if it is possible, then do biological systems possess specificity in this respect?
As we have seen above space organization is first of all the creation of a system of barriers. For one-dimensional time the analog of such barriers can be only irreversibility. But irreversibility can be of quite a different kind...
There is a statistical irreversibility described by the second law of thermodynamics. Here all the transitions between the elementary states are reversible and the system arrives statistically only (in the absence of outer exposures) into its most probable state. In this case the time organization is rather primitive: there is only one barrier that can be assimilated to the inclined plane. The system can either descent or rise (at the expense of fluctuation) along this plane, as a result it appears at the foot corresponding to the equilibrium state by all means.
However, there is irreversibility of another kind. In the physics-chemical systems it is linked to the bifurcational unstability farther from the equilibrium region (Prigogin 1980). This irreversibility is not statistical but dynamical and is absolute to some extent. The bifurcational barrier can be compared with a wall in which there is a hole provided with the valve opening only to one side. The return into the initial state if it is possible then only along hysteresis loop, i.e., through other valve or past the wall.
Such absolute irreversibility is in principle universal in the biological systems although it is not always linked with the bifurcations. For example, the transition from one stage of mitosis to the other one is not bifurcational because it does not suggest any branching of trajectories, and at the same time it is irreversible in dynamic sense as the transitions between the elementary states are irreversible, which is manifested in the irreversibility of trajectories of single organells, overmolecular complexes and even single molecules. In this case, if bifurcational barriers in the dynamics of this or that physics-chemical system alternate with the sections of determinate, and, hence, dynamically reversible trajectories, dynamically irreversible transitions in biological systems are extended much wider. Such processes as metabolism, reproduction, morphogenesis, ecological succession, and species evolution are practically continuous sequences of similar transitions.
It tells about the highest organization of biological time: every such irreversible transition is a barrier which can be compared with a wall and a valve. The availability of cassets of such barriers results not only in absolute irreversibility but in canalizing or chreodicity (Waddington 1968) of biological processes.
Such a high degree of time organization is a specific property of just biological systems. Differences of animate and inanimate nature in the organizing of space has a quantity character but differences in time organization are qualitative.
Every living thing is distinguished not only by unmeasurably great number of time barriers. That these barriers are essentially different is significantly important as, on one hand, they are not statistical, and, on the other hand, - not bifurcational. Actually here we have come across a new and third type of irreversibility. And if the second law of thermodynamics for isolated systems is in the basis of the first type and there are the bifurcations far from the thermodynamic equilibrium are in the basis of the second one, then, what is the nature of the third type stipulating high organization of the biological time? In the section below we shall try to answer this question.
2. The structure of the biological present and determinancy by future
If we take into account the "Occam's rasor", "Zeus sickle" or other emasculate instruments, we can ignore the hypothesis of the existence of certain "vis vitalis" and, hence, can accept that there is nothing except atoms and the forces of the interaction among them in the vital body, we can inevitably come to a conclusion that among all pluralities of microstates of this ensemble of atoms there exists a type that corresponds to the vital ensemble macrostate. On the other hand, based on the well-known Principle of Redy which states the impossibility of abiogenesis (Vernadsky 1924), spontaneous origination of microstates corresponding to life is impossible in the sense that it is extremely improbable.
However, such microstates always appear in the processes of metabolism, growth and reproduction in vital systems. Hence, it follows that even at the level "microworld (atoms, molecules) - world under a microscope (cells)" macrostate (life) determines microstates which maintains the life and not vice versa as is usually the case in physics and chemistry. At higher levels of vital organization it is more obvious and was noted many times by the researchers.
The first of them is probably embryologist G.Driesch who formulated his famous principle at the beginning of this century (Driesch 1919). According to this principle the fate of the embryo cell (i.e., its further development that will lay the foundation of certain tissue or an organ of a mature organism) depends, in any case at earlier stages of embryogenesis, only on the position of this cell in the emryo as a whole.
The principle of equifinality by L.von Bertalanffy (1962) can be set in this line. It states that in developing biological systems rather different original states result in one and the same final state while developing. Such equifinality is in contrary to both bifurcation and the transition to thermodynamic equilibrium (as far as the final state is not only unequilibrium but, as a rule, significantly farther from the equilibrium, than any of the initial states),which can be provided only in the case when the whole determines the behavior of its parts.
Without such kind of determinance it is even difficult to imagine the existence in the biological systems of chreods postulated by C.Waddington. Chreod by Waddington is a stable, canalized trajectory of the system development as a whole (Waddington 1968), and only the whole can provide such a trajectory stability by properly governing the analogous trajectories of its parts.
This phenomenon, when the whole determines the behavior of its parts, was specified by us as one of the distinguished properties of alive and was named as omnicausality (Mikhailovsky 1988) in contrast to particausality, i.e., determinance of the whole from its parts characteristic for physics-chemical systems.
The most important difference of omnicausal systems from particausal ones is the change of the entropy sign. In particausal systems entropy on the definition of J.von Neumann, corresponds to the "amount of (microscopic) information that is missing in the (macroscopic) description" (Neumann 1956). But in omnicausal systems macrostate, as it will be stated below, is richer with information than any single microstate. Therefore, at transition from micro- to macrolevel the information is not lost but acquired, which results in negative entropy value in such systems as it was shown before (Mikhailovsky 1981).
Two questions arise here at once. First, in what way can macrostate of the molecular ensemble determine its microstates and, second, by what is this macrostate informationally richer of each specific microstate?
Let us begin with the first one.
A complete description of any microstate is its state function (y-function), which modulus square is interpreted as probability density. It presents itself the result of interaction of y-functions of single particles. Therefore, any rather specific microstate providing the realization of rather improbable macrostate corresponds to a special type of y-function. It is possible to abruptly increase the probability of such macrostate only by re-normalization of probabilities both microstates which are supposed to be equally probable by the classic theory and the states of single particles (which is finally the same).
Thus, living macrostate of the biological system provides the realization of the corresponding microstates by means of re-normalization of probabilities as a result of which the circle of possible microstates and, hence, macrostates abruptly narrows, its mode can shift to the "tail" of the distribution. Such an effect can arise as a result of multiple interactions of the initial (a priori) function of distribution of probabilities for all possible microstates which in complicated biological systems are not equally probable, and the probability filter by means of which macrostate performs omnicausal determinance. Bayes formula (Nalimov 1981) can be used here as a mathematical model:
![]() , (2.1)
, (2.1)
where: ![]() - is the distribution function of the living state of the ensemble m as a result of the probability filter effect, k - is the constant necessary from the conditions of normalizing, p(m) - is a priori distibution function of the ensemble m ,
- is the distribution function of the living state of the ensemble m as a result of the probability filter effect, k - is the constant necessary from the conditions of normalizing, p(m) - is a priori distibution function of the ensemble m ,![]() - is the distribution function disclosing what kind of states of the ensemble m the probability filter y selects as living ones.
- is the distribution function disclosing what kind of states of the ensemble m the probability filter y selects as living ones.
For single particles (elements) similar re-normalization is expressed in the decrease up to zero of the probabilities of the overwelming number of possible directions and speeds of motions.
Such re-normalization is the characteristic for all types of omnicausal systems. For example, the collective affect the individual's behavior, directing to zero the probabilities of these actions and abruptly increasing the probabilities of others. In this case force effects are not required from the collective, as a rule the individual can only represent himself in one way. The cells behave themselves in the organism not in the same way as in cell culture and these differences cannot be always explained by the hormonal effect of the organism. In the same way the behavior of the population isolated from the natural environment (for example, the population of domesticated animals or plants) differ greatly from its behavior in nature. It is easy to suggest similar examples.
Is the approach of Bayes in all these cases only a suitable mathematical model or does it reflect the essence of re-normalization of probabilities process?
The first alternative makes the postulate of the unknown types of interaction in biological systems because the interaction known in physics does not seem to fit here. The problem in this case is similar to the one of hidden parameters in quantum mechanics (Feynman 1967; d'Espagnat 1978).
The second alternative leads to the idea of immediate interaction of y-function of macrostate (let's name it w-function) with y-function of microstate. The notion of w-function has the content only when this w-function is marked in the macroworld. Otherwise w є y.

Fig. 1. The simplest model of automonitoring system (see text for explanation).
To demonstrate the latter statement let us consider the system from television set, a videocamera located in front of the television screen and analyzer connected to the videocamera at the input and to the television set at the output (Fig.1). The arrangement of this type is called "video feedback" which is used at the analog modelling of unbalanced and stimulated media (Abraham 1976). Let there be a circumference on the screen of the "video feedback". Due to the noise the glowing dots are situated not only on the circumference, part of them is chaotically scattered on the screen. But the analyzer can isolate a circumference in a proper form (it is marked for it) out of the signal progressing from the videocamera and input it to the television set. Actually, in this model slightly noised image is the analog of y-function and the ideal circumference which the analyzer "learns" is the analog of w-function. Being supplied to the television set input this ideal circumference makes re-normalization of probabilities cutting microstate noise. As a result the television screen will maintain for unrestricted time a stable circumference image that would plunge in a noise with the time without the analyzer.
The characteristic macrostate of the biological system for itself is obviously marked, and life, as far as it exists, is supported by the automonitoring system whose rough preimage has just been discussed.
The dynamics of microstates is defined by the equation of Schrцdinger for y-function. For the biological system it is fantastically complicated and is not solved analytically but objectively has a definite form and certain numerical solutions. The dynamics of macrostates must be defined by the equations for the w-function. When the form of y-function is not degenerated due to some parameters the notion of w-function loses its sense (w є y), but if it is strongly degenerated it is possible to single out (although not single-valued) the ordered, semantic element from it which is just w-function not equal to y.
When the sky is covered fully with clouds it is perceived by us simply as noise that does not carry any signal except the warning of possible rain. If there are single running clouds we can see from the outlines of clouds (although ambiguously) the images of animals, of people, of architectural structures, etc. If we could influence the form of clouds, we could reveal better an image that is marked for us and maintain it afterwards. There would appear w-system, i.e., the system with w-function.
The dynamics of w-system is described by the system of equations for the dynamics of y- and w-functions. In the examples with clouds and "video feedback" such system of equations gives stable solution in a point. Similar solutions occur for the biological systems but only under specific conditions (cysts, organisms in diapause, steady eggs, seeds, etc.). All of them are the systems without time. But the overwhelming number of biological systems are metabolizing, developing and producing, i.e., the systems with time. The time in the system of automonitoring can appear only in the conditions when the solution of the system of w-y-equations became a stable limited cycle. In this case turning to "video feedback" the semantic image, "geschtalt" is not a hardened image but something similar to a film and the given biological system suspects its plot as present. In other words, biological present possesses of a certain time "thickness".
And here we obtain the answer to the second of the set questions above. Possessing time "thickness", alive macrostate is described by a certain succession of certain and in a certain order replacing each other's microstates. It in this way is informationally richer than any single of them. Moreover, microstates composing biological present are not an alternative. To realize living macrostate the realization of each of them is necessary in a certain succession. Therefore, by calculating statistical weight of such a state (its logarithm due to Boltzmann equation is equal to the entropy with the accuracy up to a constant) we must not sum up the probabilities of alternative microstates but multiply conditional probabilities of all succession microstates composing the "thickness" of present for the given living macrostate. This multiplication results in the statistical weight value less than one and, hence, to the negative value of entropy (Mikhailovsky 1981). For such an actually negative entropy N.Kobozev suggested the name "anti-entropy" in contrast to negentropy which is as a rule explained as a negative increment of positive entropy (Kobozev 1971). We shall use this terminology in the following.
Biological present can be different for various systems by its duration in physical time. For a cell the "thickness" of the present is minimal and for the biosphere - maximal. But at all levels biological (systemic) present includes both physical past and physical future and among them past-future at the level of microstates. In this case physical present divides biological present into memory and preadaptation or purposefulness.
As a result at all levels of biological organization the macrostate of the living system is able to determine microstates at the expense of the fact that its present includes in addition to the physical past and present, the physical future, while microstates include only present determined (at the microlevel) by the nearest past. Living macrostate re-normalizes the probabilities of microstates by determining with their physical future which is also present for it.
The process of walking is a good model of omnicausal determinance including determinance by future. Here, unlike the processes occurring in a cell, we can perceive (with the help of devices) and describe both macrostates (movement of a body with the help of legs) and microstates (successive contractions of muscle fibers under nerve impulse effects).
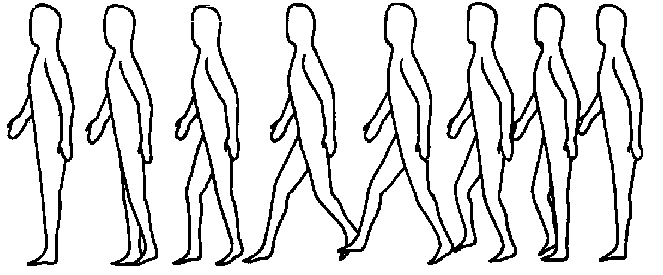
Fig. 2. A hemicycle of walking process.
Here the reason is obviously omnicausal. At first for the example of grown-ups a child receives the idea of walking. Then the process of training occurs. This process includes the selection of the most successful version of macromovements resulting in the movement of body on two legs and in this way the creation of image or plan of walking, i.e., of what we compared above with the plot. The selection takes place through memorizing of optimal versions. Mistakes are not to be repeated and, therefore, they are not memorized but forgotten and in this way are eliminated.
As a result macrostate is memorized as a certain optimal process with different versions corresponding to various external conditions (Fig. 2). This process determines arranging replacement of microstates: muscle fibres contract in such succession and in a way necessary for the walking cycle (successive movements of two legs). "Thickness" of present is equal to the time consumed for one cycle of walking.
For the observer who is at the microlevel of such a system (level of muscle fibers) everything taking place around him was perceived like "miracle": single groups of fibers either contract or relax in a certain rhythm but without any links with the processes occurring inside them. Even though such an observer found the connection of contractions with the occurring nerve impulses, all the observation would not become less miraculous for him. Improbable processes which constantly occurring before his eyes (improbable from his point of view, i.e., proceed from the natural dynamics of microstates) can be realized only due to radical re-normalization of probabilities.
Such re-normalization is a constant outer interference, namely, from macrostate side having its own plot, image, plan, into the natural dynamics of microstates. And in this case the element of "miracle", i.e., discrepancy of the observed processes at the microlevel for the second law of thermodynamics and uncertainty of future to past is introduced into the natural dynamics. The measure of this "miracle" element is anti-entropy (Kobozev 1971; Mikhailovsky 1981), and w-y-interaction (re-normalization of probabilities) is the mechanism of anti-entropy origination.
For us - observers at the level of organisms - a wonderful population "adjustment" to each other in the ecosystem or species in the biosphere stipulated by the re-normalization of probabilities effect from the higher levels of biological hierarchy is "miracle" as well. Similar process is the basis of all vital activity, the last cannot be understood completely inside its own or lower levels. The reason for such omnicausality is in the determinance of vital processes by future which is the present at the following hierarchy level. And every present at all degrees of biological hierarchy has its own and often very complicated structure which organizes the time in biological systems.
3. Two-dimensionality of time in biological systems and the hierarchy of two-dimensional biological times
Any macrostate at a certain moment of physical time can be described as a certain one-dimensional succession of values of parameters. And in this case (if we deal with particausal systems) the greater the positive entropy, i.e., the greater the number of alternative microstates realizing the same macrostate, the shorter such succession is, because it cannot be longer than the common (coinciding) part of analogous succession for all alternative microstates. In the ideal case of complete degree of order (and correspondingly, zero entropy) when only one microstate corresponds to a macrostate, and their descriptions, hence, coincide, such a succession will be of maximum length and equal to the succession length of microstate description.
But for omnicausal and in particular biological systems, such description of macrostate is not sufficient. Because macrostate in this case as we assured above, is an ordered succession of microstates. To describe it adequately it is necessary to have not one-dimensional succession but two-dimensional matrix of values of parameters. Its lines being one-dimensional descriptions of microstates forming in total the present of the given system and columns include the dynamics of the corresponding microparameters for the physical time constituting the "thickness" of this present. And it is this principal two-dimensionality of description of macrostates for omnicausal systems that stipulates the necessity of multiplicating but not summing up of conditional probabilities of all components of the matrix of microstates, which results in the value of statistical weight of microstate less than one and, hence, to the negative value of its entropy.
In this case it is possible to obtain more accurate interpretation of the anti-entropy (Titov private communication) which is based on the notion of context which is understood not only in the linguistic but in a wider meaning of this word. For the systems with positive entropy a certain set of alternative microstates corresponds to each macrostate. In the limited case of zero entropy there is a mutual correspondence between macro- and microstates. Then for the anti-entropy systems we can expect the correspondence, in a certain sense, of one microstate to some macrostates. And, in fact, in omnicausal system whose macrostate is described by two-dimensional matrix of the values of parameters, the same microstate can be in different contexts, i.e., the line of the values of the parameters corresponding to it can be the part of different matrices and correspondingly leading to different macrostates.
This is a direct consequence of the context dependence of events which we determine as microstates. For particausal systems whose entropy is positive, such events are independent of the context, which stipulates the zero time "thickness" of their macrostates. On the contrary, in omnicausal systems whose macrostates can be compared with the plot (i.e., with the text in a wider meaning of the word) there appears the phenomenon of a context, and, hence, the context dependence of events constituting the plot.
It is obvious that the same events and even their successions can be parts of quite different plots. This is also true for the biological "plots": one and the same stage of multicellular organism development, say, gastrula for Vertebrates is the beginning of the "plot" and for Coelenterata it is "outcome", i.e., the final stage of development; in the middle part of Russia (e.g., in Prioksko-Terrasny forest reserve on the bank of the Oka river) steppe sites of moderate size are the intermediary stage of ecological succession preparing the conditions for the forthcoming appearance of forest, while in the south of Ukrain - it is the final, climax stage, i.e., the "outcome" of the plot. Correspondingly, macrostates (plots) of Vertebrates and Coelenterates or forests of the middle part of Russia and the Ukranian steppes are quite different. But in any case they allow divisions according to
a) the populations, trophic groups, and etc., or either to cells, tissues, organs, and so on; and
b) events or development stages.
Thus, it is of two dimensions of description of macrostates of omnicausal systems that determines both the context dependence of their microstates (events constituting the macrostate plot) and the negative sign of their entropy and their omnicausal determinance by future and, at last, the time "thickness" of their present. It is the last property of omnicausal, and in particular biological, systems that requires a new, adequate manner of description for their time. Because of traditional physical interpretation of time in the form of one-dimensional axis for the system whose present, and, hence, macrostate, possess time "thickness", intervals of physical time less than this "thickness" are absolutely inadequate.
In fact, to follow the dynamics of macrostate of omnicausal system, we must consider it in the time discrete relative to physical, in the time which can be compressed or extended relative to the ordinary physical clock depending on the rate of processes determining the development of the "plot" of the macrostate, in the time counted by the clock, which pendulum will be the periodic reproduction of itself (usually with some insignificant deviations) by extending in physical time macrostate. The time counted in this way in case of a cell or an organism could be named ontogenetic, which is close to the notion of age.
However, the description of any onmicausal system is not restricted only to the macrostate dynamics. Macrostate itself is determined by the dynamics of microstates, i.e., by the processes occurring in another time, the time in which the lines of matrix of two-dimensional description of macrostate are ordered and which (again in case of a cell or an organism) can be named physiological. This time is counted by the events constituting the "plot" of the present of biological system and thus this plot itself is its peculiar clock. On the lowest levels of the biological hierarchy physiological time with good approximation can be considered as continuous relative to the physical time but restricted by "thickness" of the biological present for the given macrostate and, in fact, indicating the phase of the biological present. On the higher levels of hierarchy microstates (events) themselves possess a significant time "thickness", that their own dynamics is developed in time discrete relative to physical.
It should be noted that the terms "ontogenetic" or "physiological" time are relative and it is always necessary to indicate the systems for which we determine them in different cases. Moreover, as was mentioned above, the traditional biological interpretation of these terms takes place only in case with an organism or partly a cell (as far as we know its ontogenesis). In general the biological hierarchy means the hierarchy of time created in a special manner. The ontogenetic cell time can be considered as physiological time of an organism and its ontogenetic time can be interpreted as "physiological" time of population understood in genetic meaning, the "ontogenetic" time of which is usually named as phylogenetic one, and etc. (Mikhailovsky 1988).
Thus, though the biological time is in general multidimensional, it is possible to restrict every specific biological system to its two-dimensional presentation; this two-dimensionality results from the above mentioned description of macrostates of omnicausal anti-entropy system.
It should not be considered that two-dimensionality of time of the biological system is reduced only to the different scales of physiological and ontogenetic times like measuring physical time by minutes and hours. For the same value of the ontogenetic time (age) the physiological time flow can be accelerated or decelerated and even stopped (at anabiosis followed by deep cooling) under the influence of certain causes, e.g., stimulators or tranquilizers. On the other hand, at the same physiological time flow the flow of ontogenetic time can be decelerated or accelerated, depending on either the repetitive "plots" of the biological present repeat each other or introduce something new into this repetition.
In the limit, when these "plots" are absolutely equal to each other, the ontogenetic time stops: it is impossible to compose any plot out of the sequence of equal events and, keep in mind, that the ontogenetic time at the following level of hierarchy is physiological and fixes the events so that it is the "plot" of the present at this level.
It is clear that such an extreme case is never fully realized in nature but the states close to it occur, for example, in human organism at the age of about 30 - 35 when it is completely formed and the processes of aging are not manifested at all. One more example of an almost complete stop of ontogenetic time is the population of relic species in climacteric ecosystems. "Plots" of their macrostates (generations) developing in their physiological (and ontogenetic for the organisms that constitute these populations) time, practically completely repeat one another and such populations can be kept unchanged thousands and even millions of years (and the same, according to the value of magnitude, number of generations). Their ontogenetic (i.e., in this case phylogenetic) time has practically stopped.
On the example of populations it is possible to follow almost complete independence of the processes occurring in their ontogenetic time upon those that occur in time that is physiological at this level. In fact, as far as there are no clear indication that modifying variations are inherited, the whole "plot" of the population present (the development of one generation) makes no influence on its development in phylogenetic (ontogenetic for it) time. Like independence of times from one another takes place at other levels of the biological hierarchy but it is not clearly manifested there.
The opposite is not true: the processes occurring in the ontogenetic time influence the "plot" of the present developing in the physiological time and it is the omnicausal determinance itself, however, such influence is manifested in the scales of physical time much greater than the "thickness" of the present for the given system. Hence, for the time scales commensurable with the "thickness" of present it is possible to say about the independence of the processes taking place in physiological and ontogenetic times, i.e., clocks counting off them and, hence, about the independence (orthogonality) of these times themselves as components of two-dimensional time of the biological system. We have to decide the problem dealing with the manner of presentation of such two-dimensional time and its orthogonal components.
4. Presentation of two-dimensional biological time by means of complex values
From the above mentioned it follows that the moment of two-dimensional biological time can be compared with a point on the plane; ontogenetic and physiological times corresponding to the biological system are the orthogonal coordinate axes of this plane. But these two dimensions of biological times cannot be considered as completely independent: a certain link in the scales of the ontogenetic and physiological time can be observed. The time run of physiological clocks is decelerated with the flow of the ontogenetic time (with the system age), i.e., the processes determining its flow are decelerated relative to some standard physical clocks.
This phenomenon takes place at the most different levels of biological hierarchy: in the cultures of microbes and Protozoa, as they developed and a curve of their number flattens out, the tempo of cell division is decelerated a few times; in multicellular organisms the tempo of metabolic processes is decelerated with age; as to ecosystems the rate of the substance turnover, at the expense of complication of food network and elongation of real food chains, etc., is decelerated as it approaches the climax. Sometimes this process is shaded by the constant rhythms (circadian or annual) that are imposed to the biological system, but nevertheless the general tendency remains as it is. Moreover, just in those periods of development when such deceleration is almost insignificant the ontogenetic time practically stops and this fact was discussed above.
From the examples given it is seen that the negative acceleration (i.e., deceleration) of physiological clocks, in fact, is equivalent to the positive increment of reading (i.e., the run) of the ontogenetic clocks. In other words, the deceleration of physiological (for the given system) processes expressed by a fraction (where the denominator is negative square of physiological time increment) is equivalent to the rate of its ontogenetic processes which has positive ontogenetic time increment as its denominator.
Similar connection takes place between imaginary and real quantities: the negative square of the imaginary quantity is a positive real quantity. This makes one to think that the coordinate plane whose points correspond to the moments of two-dimensional biological time can be interpreted as a complex plane and its imaginary axis is presented by the physiological time, and the real one - by the ontogenetic time. In this case the region of determination of two-dimensional time of the given biological system is restricted along the imaginary axis by the "thickness" of its present and along the real one by its maximum age due to ontogenetic scale. Moreover, the scale of the real axis is discrete and equally powerful for the set of integral numbers. And for higher levels of the biological hierarchy that of the imaginary axis is discrete as well. Such scales, as it is possible to say, are the counters of cycles of present either on this level of hierarchy (real axis) or on the previous one (imaginary axis).
Thus, two-dimensional time of the given biological system can be presented in the form of a complex value with the real and imaginary parts equal to the values of ontogenetic and physiological time respectively.
Of course, the ideas dealt with cannot be considered as the basis for such presentation. They only indicate the possibility of applying this mathematical interpretation here. The efficiency of such an application will be determined only by its results. For example, the complex presentation of the biological time allows us to express within the range of one formalism both cyclic and exponential (in the general case described by the sum of exponents) characters of dynamics to which the overwhelming number of vital manifestations are reduced. The following is the example for illustration.
5. The dynamics equation for open biological systems in complex time
It is well known that biological systems possess high stability for not too strong environment perturbations. This stability determined in private life as vitality has homeoretic character and is stipulated by creodicity of their trajectories in the phase space. Furthermore in the vicinity of a stable state (or a stable trajectory) it is possible to linearize the dependence between thermodynamic flows and the forces generated by them unlike the systems with bifurcational instabilities where such dependence does not occur.
In particular, for the total energy flow related to the biomass unit a gradient of the specific total energy will correspond to its generating force. If we consider the total energy flow between the system and its environment, the gradient will turn out to be the difference of specific total energies of the system and the environment.
From these considerations and assuming the specific total energy of the environment equal to zero we can postulate the following equation:
![]() , (5.1)
, (5.1)
where e - is the specific total energy of the system and k is a constant.
Now, by introducing a complex biological time (t) as an argument, we obtain instead of (5.1) the following equation:
![]() . (5.2)
. (5.2)
Complex time (t) in the equation (5.2) can be presented, as it was mentioned above, as the sum of real ontogenetic and imaginary physiological time. In this case it is reasonable to interpret physiological time (for the cell) as the usual physical time determined, due to the above consideration, on half-interval equal to the "thickness" of the cell present. Such interpretation is the statement of the idea that cell physiology processes have been developed in the same time as all the processes in inanimated nature. And only self-reproduction of these processes provided by automonitoring and resulting in the biological present, assuming the "plot" and "thickness", takes the cell and other biological systems out of the traditional framework of one-dimensional time. In other words, for the limits of time interval less than the "thickness" of its system present it is impossible to speak of the life of this or that biological system, and, hence, about the specificity of its system time.
On the other hand, the ontogenetic time of open biological system is the value on which the development of the given system is determined. This development is, as a rule, followed by the growth, i.e., the increase of biomass. The biomass is the simplest and easily measured quantitative characteristics of ontogenetic development. Therefore, in the first approximation at any rate (by neglecting ontogenetic time discreteness, i.e., by neglecting biomass growth beyond the "thickness" of present), it is suitable to measure ontogenetic time in the units of biomass (B). If we want to keep the usual time units (hours, days, months or years) for ontogenetic time, then, biomass (measuring in energy units) should be divided by the constant having the power dimension. Such constant (![]() ) can be interpreted as the growth rate at the moment of originating (birth moment) of the given system. Then t = B/p0 + it, and "it" has been determined at the half-interval equals to the "thickness" of present for the system given.
) can be interpreted as the growth rate at the moment of originating (birth moment) of the given system. Then t = B/p0 + it, and "it" has been determined at the half-interval equals to the "thickness" of present for the system given.
As a result the equation (5.2) will take the form:
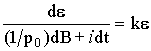 . (5.3)
. (5.3)
Let us consider the dynamics of the open biological system under the conditions when ontogenetic time practically stopped, i.e., the biomass growth is equal to zero (dB=0). Then the equation (5.3) will be simplified:
![]() . (5.4)
. (5.4)
By integrating the equation (5.4) we obtain the one for specific total energy dynamics under these conditions:
![]() , (5.5)
, (5.5)
where C - is the constant of integration.
Such oscillating exponential curve describes those cyclic processes in the biological systems that are usually named in chronobiology as "biological clock". It goes without saying that the harmonic type for solution (5.5) is idealised: in real biological systems the cyclic processes are of more complicated character, however, they can always be expanded in a Fourier series, presented as the sum of harmonic oscillations.
Now let us consider the dynamics of one and the same event from the "plot" of the present in ontogenetic time. In this case, t determined at the half-interval equals to the "thickness" of the present will assume one and the same value every time (i.e., for every subsequent cycle of the present). In other words, dt = 0. Then from equation (5.3) we have
![]() or
or ![]() . (5.6).
. (5.6).
It is interesting that the equation (5.6) is none other than the basic differential equation in "Theoretical Biology" by E.Bauer which was a starting point of his analysis (Bauer 1935). The solution of this equation at the initial biomass B0 and the initial specific total energy or, as it was named by Bauer, initial potential e0 will be the following equation:
![]() .
.
And taking into account that ![]() , where E is a total energy,
, where E is a total energy,
![]() ,
,
and, hence,
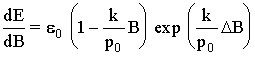 .
.
But as far as the initial energy is a positive value, the following inequality holds
![]() .
.
Thus, as Bauer has stated, at (k/p0 ) B < 1 the energy of the system as a whole will increase with that of the biomass up to a maximum attained at
![]() ,
,
where M=Bmax. Here it is seen that a cell or an organism maximum biomass is proportional to the initial rate of growth p0; a result that did not follow from Bauer theory. On the other hand, in accordance with Bauer we conclude that the increase of the cell or organism total energy at the expense of growth cannot continue to infinity but is limited by certain, its own in every case limited biomass.
The main importance of the fact, that basic Bauer differential equation has been derived as a particular case of our basic equation for the dynamics of the open biological system developed in complex time, is in the synthesis of these two approaches to the problems of theoretical biology in general, and to the growth and development regularities of biological system in particular.
Thus, thanks to the representation of two-dimensional biological time as a complex value, we succeeded in obtaining both cyclic and exponential dynamics of specific total energy in the open biological system. In our opinion, the above demonstrates the efficiency of this particular representation. As to multidimensional time presentation for all the levels of biological hierarchy as a whole, this aspect requires further development. But it should be noted that the introduction of two-dimensionality for time at every hierarchical level allows us to determine the nature of biological irreversibility as essentially only semantic one determined by the logical development of the "plot" for the given biological system.
6. Conclusion
Summarizing the above mentioned we can make the following logical chain.
Spontaneous appearance of "living" states in physics-chemical systems is impossible in that sense that it is extremely improbable. However, with the help of the biological systems this process constantly occurs. Hence, biosystems make re-normalization of probabilities of states and it is determined by higher structural level (omnicausal determinance). Such omnicausal re-normalization of probabilities, as was mentioned although not evidently by many authors, is a characteristic for all levels of the biological hierarchy from a cell up to the biosphere.
The Bayes equation can be the mathematical description of re-normalization of probabilities.
If this equation is considered as a formal model, it is necessary to look for reality, which is similar to the search of hidden parameters in quantum mechanics. However, there the hypothetical hidden parameters are meant as universal for all quanto-mechanical phenomena, while at different levels of the biological hierarchy interaction of different nature seem to act. It is not expected that the same forces set the order of molecules in a cell, deformations of layers at embryogenesis and the change of species in the process of the biosphere evolution. Thus, on this path we must not consider life as a whole phenomenon.
If Bayes approach is considered as not a model but a theory and, correspondingly, reflects up to a certain degree the essence of life as a process of re-normalization of probabilities, then we inevitably come to the idea of the reality of the function of state on the macrolevel (w-function) as probability filter. Then re-normalization of probabilities at all levels from a cell up to the biosphere will be reduced to multiplicative interaction of the functions of states for the corresponding macro-and-microlevels. For a cell the state function at the microlevel will be y-function.
The functions of state of micro-and-macrolevels are not equal to each other only when the function of macrostate is marked (designated) in the macroworld. But, as we know from practice, w-function of biosystems is not only marked (i.e., biosystems can distinguish a characteristic state for itself out of all possible ones and make automonitoring on this basis), but also possesses time "thickness" inside of which single microstates (events) advance in a certain successions ("plots"). Such time "thickness" of macrostate which, in its turn, is developed in time, being the event of the "plot" of the following hierarchy level, results in the idea of multidimensional (at every level of the biological hierarchy - two-dimensional) biological time.
On the other hand, the availability of the "plot" determines the context dependence and, hence, the semantic ambiguity of the events (states) constituting it, that is determined by the "plot logics" resulting in the semantic irreversibility that is not reduced to either statistical or bifurcational ones and organizing the time in a immensurable greater extent. In this case the events of the "plot" of the w-function at the macrolevel play the role of the designating, and their physical realization at the microlevel plays the part of the designated.
The context dependence at which the same event (microstate) can lead to quite different results (macrostates) determines the negative sign of entropy of these types of systems. The availability of omnicausal determinance makes us come to the same conclusion, because it assumes that macrostate is informationally richer than microstate in contrast to that we deal with in the systems with positive entropy. And, at last, time "thickness" of macrostate in biosystems for whose realization it is necessary the realization of not one of the alternatives but the whole set of contextually related microstates results in the value of its statistical weight < 1 and correspondingly to the value of the entropy less than zero.
Thus, omnicausality, the negative entropy sign and the consideration of macrostate function (w-function) as a probability filter not equal to the function of microstate and possessing the semantics (at any case for biosystem itself), organizing single events (microstates) into a connected "plot" - all this is only different aspects of a single process, the one of re-normalization of probabilities, which is in the basis of the phenomenon of life. Presentation of this process demands the introduction of two-dimensional time at every level of the biological hierarchy. And, at last, one of the possible manners of this two-dimensional time presentation is the use of complex values.
REFERENCES
ABRAHAM R. (1976). Simulation of cascades by video feedback. In: Lecture Notes in Mathematics.V. 525. Pp.10-14.
BAUER E.S. (1935). The Theoretical Biology. Moscow-Leningrad (in Russian).
von BERTALANFFY L. (1962). General system theory: A critical review. Gen. Syst. V.7. Pp.1-20.
DRIESCH H. (1919). Der Begriff der Organischen Form. In: Abhaundlungen zur Theoretischen Biologie. Berlin. Bd. 3. Ss.1-83.
d'ESPAGNAT B. (1976). Conceptual Foundations of Quantum Mechanics. 2-nd ed. Mass.
FEYNMAN R. (1967). The Character of Physical Laws. Cambridge,Mass.
KOBOZEV N.I. (1971). Investigations in the Field of Thermodynamics for Information and Thinking Processes. Moscow (in Russian).
MIKHAILOVSKY G.E. (1981). Negative entropy and dissipative structures initiated by the limited cycles. J. of Phys. Chem. V. 55. Pp.1877-1879 (in Russian).
MIKHAILOVSKY G.E. (1988). Description and Evaluation of Plankton Communities State. Moscow (in Russian).
NALIMOV V.V. (1981). In the Labyrinths of Language: A Mathematician's Journey. N.Y.
von NEUMANN J. (1956). Probabilistic logic and the synthesis of reliable organisms from unreliable components. In: Automata Studies. Princeton, New Jersey.
PRIGOGINE I. (1980). From Being to Becoming - Time and Complexity in the Physical Sciences. San Francisco.
VERNADSKY V.I. (1924). La Gйochimie. Paris.
VERNADSKY V.I. (1929). La Biosphere. Paris.
WADDINGTON C.H. (1968). The basis ideas of biology. In: Towards the Theoretical Biology. Birmingham. V. 1. Prolegomena. Pp.1-32.