3. Forces due to the action of time
According to N.A.Kozyrev’s causal mechanics (Kozyrev 1991), the action of time on our World is realized in cause-and-effect relations. Due to this action in the causal relations there appear small forces in addition to the conventional ones taken into account by classical mechanics. These forces are directed in such a way that they should lead to a mirror asymmetry between the cause and the effect, responsible for an objective difference between them in causal mechanics.
N.A.Kozyrev’s papers specify the values of the additional forces as applied to the case when a rotating perfect top is incorporated in the cause-and-effect link as one of the components. We would like to suggest possible generalizations to the cases of arbitrary pairs of interacting material points.

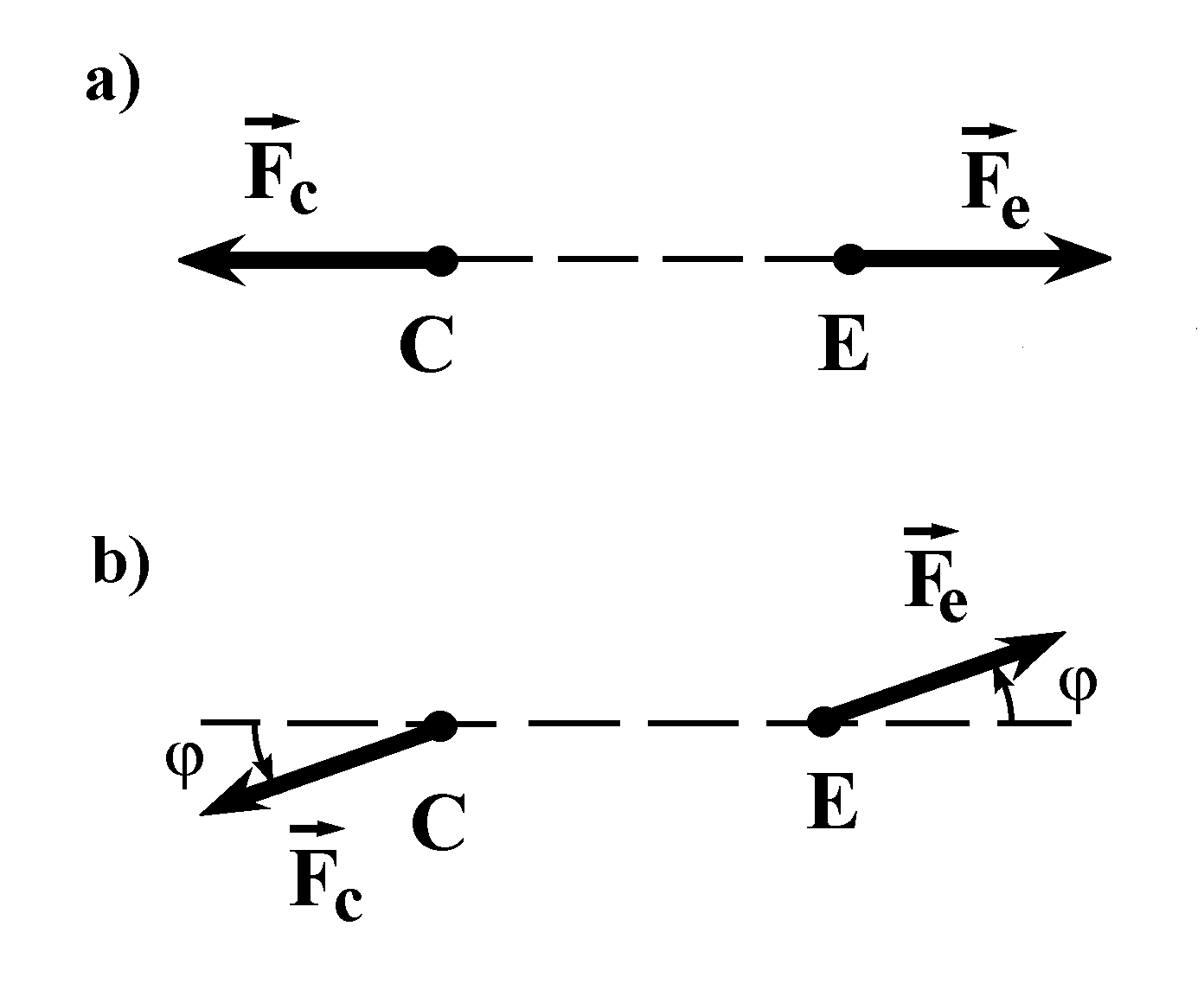
Fig.3. An elementary cause-and-effect link consisting of two material points:
a — the forces ![]() and
and ![]() having a common line of action; b — the lines of action of the forces
having a common line of action; b — the lines of action of the forces ![]() and
and ![]() are parallel but do not coincide; C — the cause, E — the effect;
are parallel but do not coincide; C — the cause, E — the effect; ![]() and
and ![]() — the action and reaction forces;
— the action and reaction forces; ![]()
Following N.A.Kozyrev, let us consider an elementary cause-and-effect link consisting of two material points, a cause point and an effect point, with no other material body between them. We shall assume that the cause point C acts on the effect point E by the force ![]() , and the effect E reacts on the cause C by the reaction force
, and the effect E reacts on the cause C by the reaction force ![]() . According to Newton’s third law the forces of action and reaction are equal in magnitude and opposite in direction, i.e.,
. According to Newton’s third law the forces of action and reaction are equal in magnitude and opposite in direction, i.e., ![]() = -
= -![]() . In addition to Newton’s third law, theoretical mechanics always assumes that the interaction forces between any two internal points of the system act along one and the same line (Polyakhov et al. 1985, p.137). As applied to the cause-and-effect link under consideration, this assumption means that the forces
. In addition to Newton’s third law, theoretical mechanics always assumes that the interaction forces between any two internal points of the system act along one and the same line (Polyakhov et al. 1985, p.137). As applied to the cause-and-effect link under consideration, this assumption means that the forces ![]() and
and ![]() are directed along the straight line connecting the points C and E (Fig.3a).
are directed along the straight line connecting the points C and E (Fig.3a).
Let us note the fact that classical mechanics does not consider the assumption of orientation of internal forces to be such a fundamental law of nature as Newton’s laws. Moreover, theories lacking such assumptions have been constructed for long in continuum mechanics, one of the branches of classical mechanics (Sedov 1983). The moment theory of elasticity, elaborated as early as at the dawn of the twentieth century, provides an example for such a theory (Nowacki 1970, Chapter 13). On breaking with that assumption, the forces of action and reaction may appear to be directed along collinear but uncoinciding lines (Fig.3b). Newton’s third law remains valid, as before, i.e., ![]() = -
= -![]() .
.
Suppose that the “interference” of time in the causal relation leads just to breaking the above assumption. Namely, let us assume that the action of time manifests itself in a deviation of the vectors of the forces ![]() and
and ![]() from the straight line by the same angle j О [0,p /2] to opposite sides. Three possible versions of such a deviation can be suggested.
from the straight line by the same angle j О [0,p /2] to opposite sides. Three possible versions of such a deviation can be suggested.
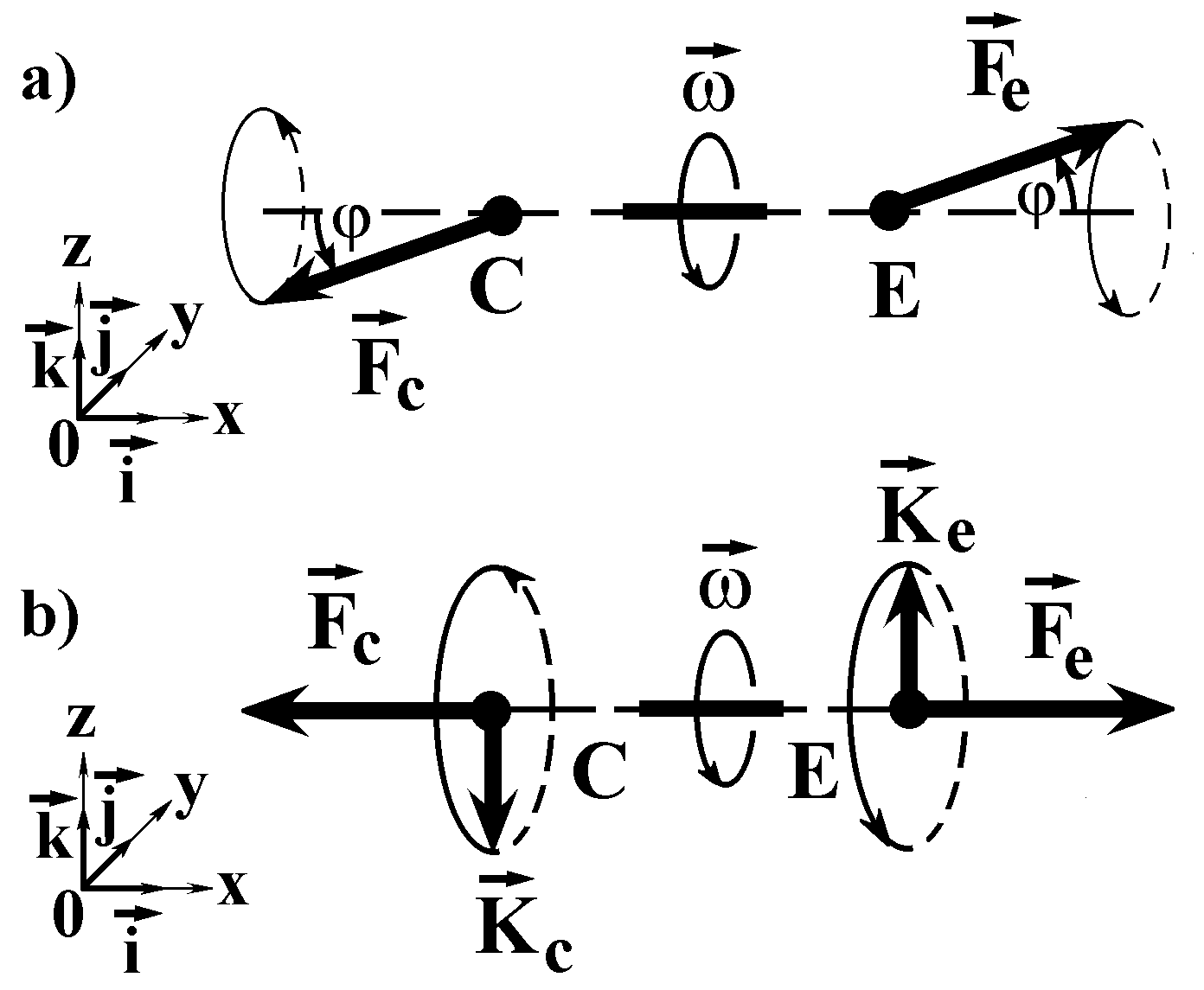
Fig.4. A possible influence of time on a causal link: a — the deflection of the forces ![]() and
and ![]() from the straight line CE by the angle j
Î
[
0,p
/
2]
with their rotation around this line with the angular velocity
from the straight line CE by the angle j
Î
[
0,p
/
2]
with their rotation around this line with the angular velocity ![]() (
(![]()
Version 1. Let the deviations of the forces ![]() and
and ![]() from the straight line CE be accompanied by their rotation about this line in the same direction with a certain angular velocity
from the straight line CE be accompanied by their rotation about this line in the same direction with a certain angular velocity ![]() (Fig.4a). In this case the two components of the cause-and-effect link turn out to be objectively different. Indeed, looking at one of the components from the place where the other is located, we see the rotation of the force vector occurring anticlockwise, and looking at the other component from where the first component is located, we see rotation of the force vector occurring clockwise. So this version relates the difference between the cause and the effect to that between the right and the left in our World, as it should be the case in accord with the fundamentals of Kozyrev’s causal mechanics.
(Fig.4a). In this case the two components of the cause-and-effect link turn out to be objectively different. Indeed, looking at one of the components from the place where the other is located, we see the rotation of the force vector occurring anticlockwise, and looking at the other component from where the first component is located, we see rotation of the force vector occurring clockwise. So this version relates the difference between the cause and the effect to that between the right and the left in our World, as it should be the case in accord with the fundamentals of Kozyrev’s causal mechanics.
Let us introduce a Cartesian right-handed rectangular coordinate system {O, x, y, z} with the Ox axis parallel to the straight line CE pointed from the cause to the effect, as shown in Fig.4a. Denote the unit vectors of the Ox, Oy, Oz coordinate axes by ![]() , respectively. Then the force
, respectively. Then the force ![]() in a position deflected from the line CE can be represented in the form of the sum of three components along the coordinate axes:
in a position deflected from the line CE can be represented in the form of the sum of three components along the coordinate axes:
![]() , (3.1)
, (3.1)
its projections on the coordinate axes being described by the formula
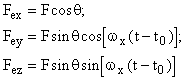 . (3.2)
. (3.2)
Here F = п ![]() п is the force magnitude; the force magnitude in this case coincides with that given by classical mechanics; q is the angle between the unit vector
п is the force magnitude; the force magnitude in this case coincides with that given by classical mechanics; q is the angle between the unit vector ![]() and the force vector
and the force vector ![]() , 0 Ј q Ј p ( q = j for 0 Ј q Ј p / 2 , which occurs when the effect repels the cause, and q = p - j for p / 2 Ј q Ј p , which corresponds to attraction of the effect to the cause, where j is the deflection angle of the forces
, 0 Ј q Ј p ( q = j for 0 Ј q Ј p / 2 , which occurs when the effect repels the cause, and q = p - j for p / 2 Ј q Ј p , which corresponds to attraction of the effect to the cause, where j is the deflection angle of the forces ![]() and
and ![]() from the line CE);
from the line CE); ![]() is the projection of the angular velocity pseudovector
is the projection of the angular velocity pseudovector ![]() on the Ox axis (in our case
on the Ox axis (in our case ![]() ); t0 is a time parameter characterizing the rotation phase of the force
); t0 is a time parameter characterizing the rotation phase of the force ![]() . Certainly the force
. Certainly the force ![]() may be decomposed into similar components differing from those of
may be decomposed into similar components differing from those of ![]() only by sign.
only by sign.
For a small angle j (j < < 1 ) this version of the action of time can be presented (in the linear approximation in j ) as the appearance of small, oppositely directed additional forces ![]() and
and ![]() applied to the cause C and the effect E. We denote these forces by the letter K after Kozyrev’s name. The forces
applied to the cause C and the effect E. We denote these forces by the letter K after Kozyrev’s name. The forces ![]() and
and ![]() are orthogonal to the straight line CE, rotate about it with the angular velocity
are orthogonal to the straight line CE, rotate about it with the angular velocity ![]() and satisfy the relations
and satisfy the relations
![]() , (3.3)
, (3.3)
where the forces ![]() and
and ![]() are now directed along the straight line CE (Fig.4b). Here
are now directed along the straight line CE (Fig.4b). Here
![]() .
.
As seen from (3.2), in the version under consideration the three scalar quantities: the angle j (or q ), the angular velocity projection w x and the parameter t0 are characteristics of the action of time on the causal connection. The parameter t0, setting the force rotation phase, most likely should not manifest itself in macroscopic experiments (in a similar way phases of thermal oscillations of atoms fail to affect the macroscopic properties of bodies). Thus only two quantities: j and w x may be regarded as essential characteristics of the action of time.
Assume that these quantities are related by a dependence close to
![]() , (3.4)
, (3.4)
where ![]() is the absolute value of the angular velocity pseudovector
is the absolute value of the angular velocity pseudovector ![]() ; w 0 is a constant of frequency dimension. Then at j = 0 we obtain the case studied by theoretical mechanics, with the system being purely determinate. On the contrary, at j = p / 2 the causal action completely disappears and the system becomes absolutely indeterminate (the latter follows from the fact that at j = p / 2 the forces
; w 0 is a constant of frequency dimension. Then at j = 0 we obtain the case studied by theoretical mechanics, with the system being purely determinate. On the contrary, at j = p / 2 the causal action completely disappears and the system becomes absolutely indeterminate (the latter follows from the fact that at j = p / 2 the forces ![]() and
and ![]() are directed perpendicular to the straight line CE and rotate about it infinitely rapidly and therefore their time averages over any time interval turn out to be exactly zero). The existence of the two limiting states of a system, one strictly determinate and another absolutely indeterminate, is in complete agreement with the ideas of causal mechanics.
are directed perpendicular to the straight line CE and rotate about it infinitely rapidly and therefore their time averages over any time interval turn out to be exactly zero). The existence of the two limiting states of a system, one strictly determinate and another absolutely indeterminate, is in complete agreement with the ideas of causal mechanics.
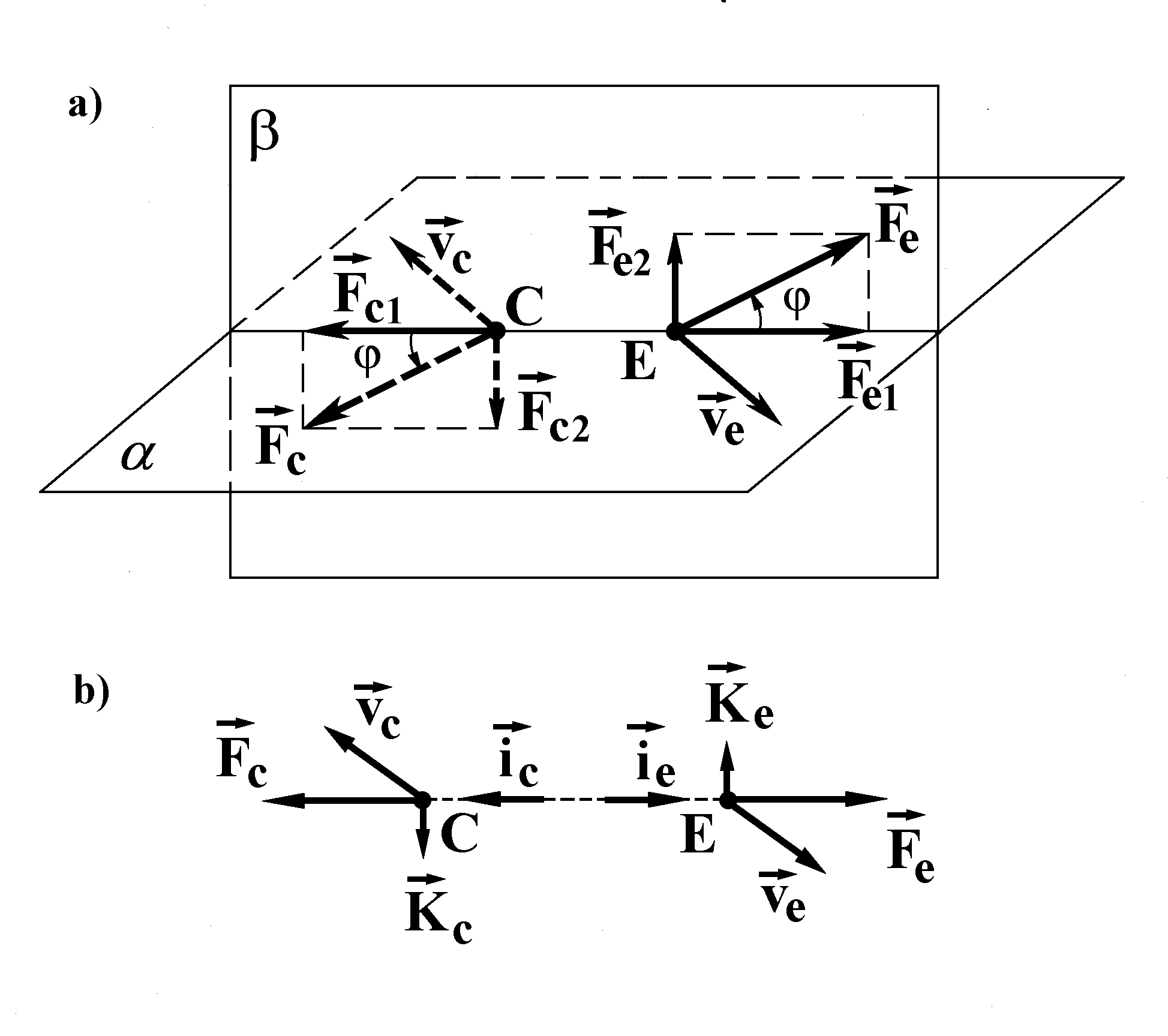
Fig.5. One more possible action of time on a causal link:
a — the deflection of the forces ![]()
Version 2. Let the forces ![]() and
and ![]() deviate from the straight line CE as follows. If the relative motion velocity of the cause C and the effect E is directed along the straight line CE or equal to zero, a deviation is absent. If the relative velocity of the points C and E is directed at a certain angle to the straight line CE, there occurs a deviation of the forces in the plane perpendicular to another plane containing the vector of relative velocity and the straight line CE. As this takes place, the forces
deviate from the straight line CE as follows. If the relative motion velocity of the cause C and the effect E is directed along the straight line CE or equal to zero, a deviation is absent. If the relative velocity of the points C and E is directed at a certain angle to the straight line CE, there occurs a deviation of the forces in the plane perpendicular to another plane containing the vector of relative velocity and the straight line CE. As this takes place, the forces ![]() and
and ![]() deflect from the straight line CE in opposite directions by the same angle, as we have agreed before (Fig.5a).
deflect from the straight line CE in opposite directions by the same angle, as we have agreed before (Fig.5a).
One of the two possible directions of force deflection in the above plane can be defined for each element of the cause-and-effect link in the following way. Consider three vectors: (i) the velocity with which the element under consideration moves with respect to the other one, (ii) the component of the force acting on it, directed along the straight line CE, and (iii) the component of the same force directed perpendicular to the line CE. Let us ascribe numbers to these vectors in the same succession as they are listed and assume that a deflection of the force from the straight line occurs in such a direction that the above ordered triad of vectors form a left frame for the cause point and a right one for the effect point. We shall assume that the force deflection angle from the straight line CE depends on the relative motion velocity of the cause and the effect in such a way that it vanishes when the relative velocity vector direction approaches that of the line CE.
Let us consider this version in more detail for the case of small j. In this case the force deflection from the line CE may be regarded as a consequence of action of the small additional forces ![]() and
and ![]() directed perpendicular to the line CE and connected with the angle j by the relations
directed perpendicular to the line CE and connected with the angle j by the relations
![]() (3.5)
(3.5)
(Fig.5b). We shall assume that the additional forces are described by the expressions
![]() ; (3.6)
; (3.6)
![]() , (3.7)
, (3.7)
where the forces of action (![]() ) and reaction (
) and reaction (![]() ) are directed along the line CE;
) are directed along the line CE; ![]() is the velocity of the effect point E with respect to the cause point C;
is the velocity of the effect point E with respect to the cause point C; ![]() ; c2 is a pseudoscalar parameter of velocity dimension, c2 > 0 in a right-handed coordinate frame (the pseudoscalarity of c2 is required to compensate the pseudovector nature of the vector product). From
; c2 is a pseudoscalar parameter of velocity dimension, c2 > 0 in a right-handed coordinate frame (the pseudoscalarity of c2 is required to compensate the pseudovector nature of the vector product). From ![]() = -
= -![]() and
and ![]() it follows that
it follows that ![]() = -
= -![]() , as expected. Since we are considering the case j << 1, one can write with (3.5), (3.6):
, as expected. Since we are considering the case j << 1, one can write with (3.5), (3.6):
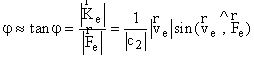 , (3.8)
, (3.8)
therefore the condition ![]() should be satisfied. For simplicity we shall assume that
should be satisfied. For simplicity we shall assume that ![]() . We shall discuss Eqs. (3.6), (3.7) below, after describing the third possible version of the action of time on the causal connection.
. We shall discuss Eqs. (3.6), (3.7) below, after describing the third possible version of the action of time on the causal connection.
Version 3. Assume that the forces ![]() and
and ![]() deflect from the straight line CE in the same way as in Version 2 with the only exception: the deflection direction is determined by another ordered triad of vectors. Namely, let us take the following three vectors: (i) that of relative velocity of the element under consideration of the cause-and-effect link; (ii) the unit vector lying on the straight line CE and pointed towards the given element (off the other); (iii) the component of the force acting on the given element, directed perpendicular to the line CE. (In Version 2 the force component directed along the straight line CE was taken as the second vector.) Assume that the deflection of the force from the straight line CE occurs in such a way that the above three vectors, numbered in the above order, form a left frame for the cause point and a right one for the effect point. The force deflection angle j is assumed to be the same as in Version 2.
deflect from the straight line CE in the same way as in Version 2 with the only exception: the deflection direction is determined by another ordered triad of vectors. Namely, let us take the following three vectors: (i) that of relative velocity of the element under consideration of the cause-and-effect link; (ii) the unit vector lying on the straight line CE and pointed towards the given element (off the other); (iii) the component of the force acting on the given element, directed perpendicular to the line CE. (In Version 2 the force component directed along the straight line CE was taken as the second vector.) Assume that the deflection of the force from the straight line CE occurs in such a way that the above three vectors, numbered in the above order, form a left frame for the cause point and a right one for the effect point. The force deflection angle j is assumed to be the same as in Version 2.
For small j one can again replace the deflections of the forces ![]() and
and ![]() from the line CE by adding small additional forces
from the line CE by adding small additional forces ![]() and
and ![]() perpendicular to this line and satisfying the relations (3.5). We shall assume that these forces are described by the expressions
perpendicular to this line and satisfying the relations (3.5). We shall assume that these forces are described by the expressions
![]() ; (3.9)
; (3.9)
![]() , (3.10)
, (3.10)
where ![]() ;
; ![]() and
and ![]() are the unit vectors lying on the straight line CE, so that
are the unit vectors lying on the straight line CE, so that ![]() is drawn from the point C towards the point E, and
is drawn from the point C towards the point E, and ![]() is drawn from the point E towards the point C (
is drawn from the point E towards the point C (![]() = -
= -![]() ); the other notations are the same as in Eqs. (3.6) and (3.7) (see Fig.5b). Here, as well as in Version 2, we assume that the condition п
); the other notations are the same as in Eqs. (3.6) and (3.7) (see Fig.5b). Here, as well as in Version 2, we assume that the condition п ![]() п <<п c2п is fulfilled.
п <<п c2п is fulfilled.
Now let us consider a particular case. Let the cause point C be at rest in a certain inertial frame of reference, and the effect point E revolve uniformly about it along a circle centered at the point C. In this case the relative velocity ![]() is perpendicular to the straight line CE and directed along a tangent to the circle, therefore Eqs. (3.9), (3.10) can be transformed to yield
is perpendicular to the straight line CE and directed along a tangent to the circle, therefore Eqs. (3.9), (3.10) can be transformed to yield
![]() ; (3.11)
; (3.11)
![]() , (3.12)
, (3.12)
where ![]() ;
; ![]() is a unit pseudovector perpendicular to the vectors
is a unit pseudovector perpendicular to the vectors ![]() and
and ![]() and pointed in the same direction as the pseudovector
and pointed in the same direction as the pseudovector ![]() ґ
ґ ![]() . Equations (3.11) and (3.12) are in agreement with those for the additional forces in causal mechanics (Kozyrev 1991). It is by similarity with the latter that we introduced the notation c2 for the parameter entering in the right-hand sides of our formula. Note that if the cause-effect interaction is of repulsive nature, then
. Equations (3.11) and (3.12) are in agreement with those for the additional forces in causal mechanics (Kozyrev 1991). It is by similarity with the latter that we introduced the notation c2 for the parameter entering in the right-hand sides of our formula. Note that if the cause-effect interaction is of repulsive nature, then ![]() , and Eqs. (3.6) and (3.7) from Version 2 acquire the form (3.9), (3.10). Therefore in this particular case they can be converted to (3.11), (3.12) as well. Thus, Versions 2 and 3 proposed for the action of time on the cause-and-effect connection may be regarded as possible immediate generalizations of the corresponding propositions of causal mechanics.
, and Eqs. (3.6) and (3.7) from Version 2 acquire the form (3.9), (3.10). Therefore in this particular case they can be converted to (3.11), (3.12) as well. Thus, Versions 2 and 3 proposed for the action of time on the cause-and-effect connection may be regarded as possible immediate generalizations of the corresponding propositions of causal mechanics.
It should be noted that the difference between Versions 2 and 3 manifests itself most noticeably in the case of a sign-variable interaction between the cause and the effect: as signs of the forces ![]() and
and ![]() change, the additional forces
change, the additional forces ![]() and
and ![]() in Version 2 change signs as well, whereas in Version 3 they remain unchanged. Also note that, strictly speaking, the appearance of additional forces of a certain magnitude and a deflection of the “classical” forces by the angle determined by Eqs. (3.5), are not identical results. However, for additional forces much less in magnitude than the “classical” ones these results differ by second-order small quantities and are indistinguishable within the measurement accuracy achieved in N.A.Kozyrev’s experiments.
in Version 2 change signs as well, whereas in Version 3 they remain unchanged. Also note that, strictly speaking, the appearance of additional forces of a certain magnitude and a deflection of the “classical” forces by the angle determined by Eqs. (3.5), are not identical results. However, for additional forces much less in magnitude than the “classical” ones these results differ by second-order small quantities and are indistinguishable within the measurement accuracy achieved in N.A.Kozyrev’s experiments.
A distinctive feature of the additional forces ![]() and
and ![]() introduced in Versions 2 and 3, is that in total they do not perform work over the cause-and-effect link.
introduced in Versions 2 and 3, is that in total they do not perform work over the cause-and-effect link.
Indeed, the total increment of work D A of these forces for a short time interval D t amounts to
![]() (3.13)
(3.13)
where ![]() and
and ![]() are the effect and cause velocities with respect to the inertial frame of reference under consideration. Taking into account that
are the effect and cause velocities with respect to the inertial frame of reference under consideration. Taking into account that ![]() = -
= -![]() and that the effect moves with respect to the cause with the velocity
and that the effect moves with respect to the cause with the velocity ![]() =
=![]() -
-![]() , we obtain from (3.13):
, we obtain from (3.13):
![]() .
.
Since the additional force ![]() , according to Eqs. (3.6), (3.9), is perpendicular to the velocity vector
, according to Eqs. (3.6), (3.9), is perpendicular to the velocity vector ![]() , we obtain finally that D A = 0.
, we obtain finally that D A = 0.
This result is of fundamental significance. It means that no additional expenses of work are required to realize actions on the cause-and-effect link described in Versions 2 and 3. The system energy also remains unchanged under such an action. Also note that since the principal vector of the additional forces is zero, ![]() +
+![]() =
= ![]() , the total momentum of the system remains unchanged. At the same time, this action can change the angular momentum of the system and the trajectories of the cause-and-effect link elements. Probably it is just the version of the action of time on causal connections to which N.A.Kozyrev inclined as his ideas were developed. In his first publications on causal mechanics he wrote that time was able to augment the energy of a system, while in more recent papers he asserted that time, via its active physical properties, increases the order of matter, preventing (to some extent) an increase of entropy in a system, i.e., it acts as a source of negentropy in our World.
, the total momentum of the system remains unchanged. At the same time, this action can change the angular momentum of the system and the trajectories of the cause-and-effect link elements. Probably it is just the version of the action of time on causal connections to which N.A.Kozyrev inclined as his ideas were developed. In his first publications on causal mechanics he wrote that time was able to augment the energy of a system, while in more recent papers he asserted that time, via its active physical properties, increases the order of matter, preventing (to some extent) an increase of entropy in a system, i.e., it acts as a source of negentropy in our World.
Thus we have considered three possible versions of force vector deflection from the straight line connecting the interacting points. This deviation cannot be explained within the framework of classical mechanics by the properties of the cause-and-effect link itself due to its symmetry. Material points in classical mechanics have no internal structure, hence their symmetry coincides with that of a geometric point. That implies that among the elements of symmetry of a cause-and-effect link there is an infinite order rotation axis passing through the cause and effect points, and mirror symmetry planes containing the rotation axis. With these elements of symmetry available, no internal cause is able to deviate the interaction force from the rotation axis in some direction (as it is the case in Versions 2 and 3) or lead to its deviation and rotation in a certain direction (as in Version 1). Hence, from the viewpoint of classical mechanics, a deviation like those described could result only from causes external with respect to our cause-and-effect link.
The above three versions of the action of time on a cause-and-effect link are, of course, not the only possible ones. However, which of these or other possible versions reflects the reality appropriately, can be decided only from the results of special experiments.
As seen from the present section, in classical mechanics itself there exists a possibility of force deviation from the straight line connecting the interacting points (there is, however, no physical reason for such a deviation in a certain direction). Therefore Kozyrev’s causal mechanics may be regarded as a natural development of Newton’s classical mechanics.