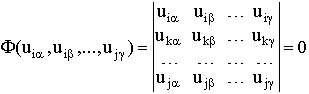 . (2)
. (2)CHAPTER 1. PHYSICS
STRUCTURE OF PHYSICAL SPACE-TIME
Yu. S. Vladimirov
This book is dedicated to studies of the concept of time; however, the author is convinced that TIME AND SPACE FORM A SINGLE WHOLE. The physical space cannot be imagined without time, as well as any discussion of time without space becomes scholastic. Moreover, this chapter asserts that the usual classical views of space and time conceal deeper concepts and relations from which both the space-time and the fundamental physical interactions are formed. Another feature of this chapter is that it rests on the RELATIONAL SPACE-TIME PARADIGM by which space and time describe only relations between material objects (events) and lose the right to exist in their absence. In this aspect the present chapter opposes the substantial views upon space and time, while some other chapters are written in the spirit of those views.
1. The present approach has been developed in the unified theory of space-time relations and physical interactions constructed by the author and called binary geometrophysics (Vladimirov 1988; Kulakov et al. 1992). It is built on the basis of binary physical structure theory (Kulakov 1968, 1971) and rests upon the ideas of the Fokker-Feynman direct interparticle action theory (Fokker 1929; Wheeler and Feynman 1945) and Kaluza-Klein type multidimensional geometric models of physical interactions (Kaluza 1921). Among the research programs represented in modern literature, the closest one to binary geometrophysics is the twistor program of R.Penrose (1968). One of the manifestations of this closeness is that in both programs the classical space-time is apprehended as a certain secondary construction to be obtained from deeper concepts used in microphysics. Second, both programs use two-component (complex) spinors (more precisely, pairs of two-component spinors) as the more primary entities. In the Penrose program they are called twistors.
However, there are significant differences between the two programs. Whereas in the Penrose program twistors and their properties are the primary concepts, in binary geometrophysics the starting premises are still deeper: they are derived from binary physical structure theory. The spinors appear as a necessary consequence from one of the key lowest rank binary structures. There exist other differences, too.
2. Since physical structure theory developed by Yu.I.Kulakov is not known widely enough, I would like to remind of its key statements. The theory assumes that there exist two sets m and n consisting of certain elements, and binary relations uia between elements belonging to different sets. Let us denote the elements of m by Latin indices and those of n by Greek ones. A relation uia is a real or complex number (a sort of metric). One obtains binary physical structure theory by postulating that, first, the relations uia obey some relationships called structure laws. The simplest thing has been assumed, namely, that these relationships are algebraic. If r elements are selected from the first set and s elements from the second one, such a relationship (law) is
F( uia , uib , ..., ujg ) = 0, (1)
where F is an algebraic function of rs variables, i.e., of all the possible relations between the elements selected from different sets. Second, it is assumed that the law (1) possesses the fundamental symmetry property: it is valid for any r elements of the first set and any s elements of the second one. The pair of numbers (r, s) is called rank of a binary structure. It turns out that these two requirements lead to a set of functional-differential equations, from which one can derive the properties of the binary relations and the possible forms of binary structure laws for rank (r, s) structures.
G.G.Mikhailichenko (1972) has shown that, for the case of real binary relations, the laws can exist only for ranks (r, r), (r, r± 1), (2,4) and (4,2). For all the other ranks there are no structures. The laws for rank (r, r) non-degenerate binary structures are expressed in terms of determinants containing the binary relations:
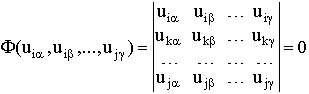 . (2)
. (2)
The binary relations are presented in the form
uia =![]() , (3)
, (3)
where il are the r-1 parameters corresponding to elements of the first set and al are the r-1 parameters corresponding to elements of the second set. Structure laws for other ranks have been obtained by Yu.I.Kulakov (1968).
3. A similar theory can be constructed using a single set of elements. In this case a rank is determined by a single integer r and the structure law for such a unary structure has the form
F( uik, uij, ..., ujp ) = 0, (4)
where an algebraic function F depends on r(r-1)/2 binary relations between r elements of the same nature. Again the fundamental symmetry principle makes it possible to formulate differential-functional equations from which the possible laws F and the forms of binary relations are obtained. However, now the equations turn out to be more complicated and the possible solutions, i.e., the structure laws, are more numerous. All of them have been found for the ranks r = 3, 4, 5 and probably 6. The studies performed by Kulakov's group have shown that all these solutions correspond to the known types of geometries whose dimensionalities n are connected with the structure ranks by the relation n = r-2. Thus, for r = 5 one obtains 10 different 3-dimensional geometries: the Euclidean, pseudo-Euclidean and Lobachevsky geometries, the Riemann geometry (of constant positive curvature), a specific simplectic geometry and some others. Among them there are some "exotic" geometries, known to very few people. Thus all these different geometries, so frequently used, can be viewed as particular cases of unary structures and the geometries themselves can be called UNARY, i.e, those determined by a single set of elements.
Kulakov's group has also shown that there are no consistent theories employing three or more sets of elements.
4. Since the theories of unary and binary structures rest on the same principles and the unary structure theories correspond to geometries, one can assert that the binary structures open a new class of geometries, BINARY GEOMETRIES. Modern physics is known to use widely different (unary) geometries in order to describe physical interactions, for instance, in the forms of general relativity, Kaluza-Klein theories, affine geometries, etc. As a new class of geometries has been discovered, binary ones, it is a natural idea to seek their applications to modern theoretical physics. Binary structure theory turns out to be simpler than that of the unary ones; moreover, it is possible to create unary structure from binary ones, while the reverse is wrong. Hence it is natural to expect that a geometrization program for physics (physical interactions) should start just from binary physical structure theory (binary geometry). That is what binary geometrophysics is aimed at.
It turns out that the very fundamentals of modern physics and space-time theory can be viewed through the prism of binary structures, i.e., it can be shown that practically all the key concepts and relations of fundamental physics may be treated in terms of the properties of the lowest rank binary structures. To achieve that it is sufficient to use complexified binary structures of symmetric ranks (r, r). Moreover, it turns out that such binary structures are already widely used in modern physics in the forms of spinors, quadratic expressions for observables in quantum mechanics and other concepts.
5. Binary structures of the lowest ranks (2,2) and (3,3) are of key significance for describing the microworld fundamentals and the classical 4-dimensional space-time. The rank (2,2) structure turns out to be embedded in the rank (3,3) structure, therefore it is natural to start from the latter. In binary geometrophysics the elements of the first set m of the rank (3,3) structure are interpreted as initial lepton states, and the elements of the second set n as final lepton states in an elementary transition of a particle between two states (Fig.1). According to the general formula (3), the binary relation uia between the two states has the form
uia = i1a1+i2a2, (5)
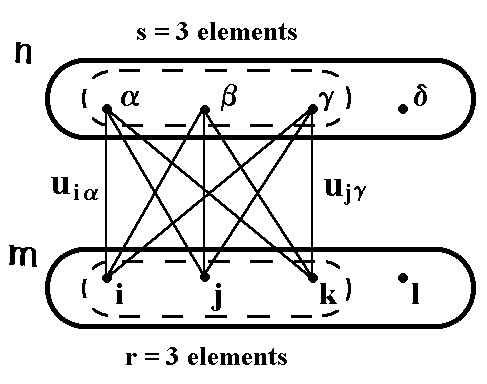
Fig. 1. The rank (3,3) complexified binary structure.
where i1 and i2 are two complex parameters put into correspondence to the first state (element i) and a1, a2 are those corresponding to element a. In other words, the states are described by vectors of a two-dimensional complex space. It is assumed that one element in each state describes a neutrino while two elements describe idealized massive leptons (electrons). The word "idealized" means that the electrons are considered to have a nonzero rest mass but no charge which, as well as the interaction itself, can be introduced only after inclusion of higher rank structures.
Within the rank (3,3) structure only free particles (leptons) can be described. The final states a and b of a free particle are expressed in terms of its initial states in the following way:
is = a*s ; ks =b*s (s = 1,2), (6)
where, as it is common to quantum mechanics, an asterisk denotes complex conjugates. The parameters is and as in (5) are defined only up to linear transformations
![]() , (7)
, (7)
where ![]() are complex transformation parameters obeying certain conditions.
are complex transformation parameters obeying certain conditions.
6. A key role in the theory of the rank (3,3) structure belongs to fundamental 2ґ 2-relations (minors from the law (2), a sort of 2-volumes), put into correspondence to two pairs of elements from different sets. They are presented in the form
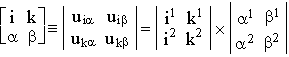 , (8)
, (8)
where the r.h.s. contains the determinants such that each was built from the element parameters of a single sort. The transformations preserving (8) must leave each of the determinants on the r.h.s. invariant. This imposes the following conditions upon the coefficients ![]() in (7):
in (7):
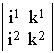 = i1k2-i2k1 = inv а
= i1k2-i2k1 = inv а ![]() =1, (9)
=1, (9)
i.e., the 6-parametric group of transformations SL(2,C), corresponding to the proper Lorentz group in the Minkowski space-time, comes into play.
The expression i1k2-i2k1 in (9) can be interpreted as an invariant metric in a 2-dimensional complex space. The vectors of that space (is and ks) are known as two-component spinors, while the invariant itself is their antisymmetric scalar product
i1k2-i2k1 є esr is kr є isks , (10)
where s = 1,2 and esr is the antisymmetric spinor metric (Rumer 1936). Similar things can be said about the conjugate space n where the metric is defined by the expression ![]() . Here and henceforth the conjugate space indices marked by dots.
. Here and henceforth the conjugate space indices marked by dots.
7. Just as in quantum theory observables are described by Hermitian operators, or in general relativity observables correspond to scalars, provided that frames of reference are defined by monads or tetrads, in binary geometrophysics a physical interpretation is realized by a transition from complexified binary structures to real unary structures (geometries). Such a transition is achieved by introducing certain matching conditions for the elements of the two sets and by determining real binary relations between the matched element sets (Fig.2).
The conditions (6) are just these matching conditions for the rank (3,3) structure. As it has been pointed out, massive leptons are characterized by four matched elements. Assuming that one lepton is characterized by the elements i, k,a ,b , and another one by the elements j, s,g ,d, the real binary relation of the two leptons a(1,2) is described by the expression
a(1,2) = ![]() , (11)
, (11)
where the symbol ![]() is defined in (8). It can be easily shown that this binary relation can be presented in the form
is defined in (8). It can be easily shown that this binary relation can be presented in the form
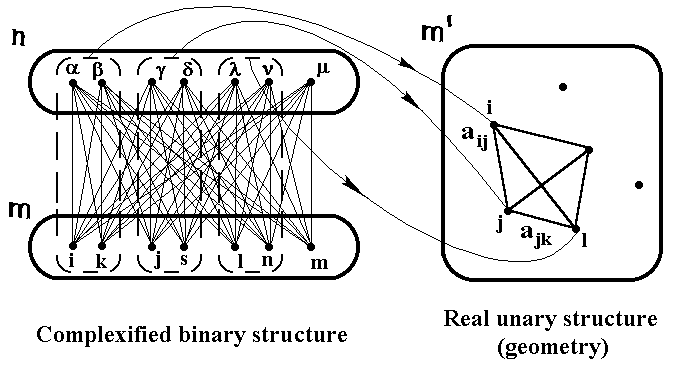
Fig. 2. A transition from a complexified binary structure to a real unary structure (geometry).
a(1,2) = ![]()
![]() , (12)
, (12)
where P(1)m for the first particle are
![]() ;
;
![]() ;
;
![]() ;
;
![]() . (13)
. (13)
Similarly P(2)m are expressed in terms of the element parameters j, s, g, d .
The components Pm from (13) are transformed under transformations (7) from the SL(2,C) group in the same way as the 4-dimensional vectors under Lorentz transformations. For massive leptons Pm are normalized to a certain quantity m02 c2:
a(1,1) = ![]() =Inv; a(2,2) =
=Inv; a(2,2) =![]() =Inv. (14)
=Inv. (14)
The real vectors Pm with the lengths (14) and the scalar product (12) determine the Lobachevsky geometry (the 3-dimensional hyperbolic geometry). In binary geometry the vectors Pm are interpreted as momenta of massive leptons and the real (unary) geometry as the momentum space. Under a proper choice of the Dirac gamma-matrix representation it is possible to present the components Pm from (13) in the form ![]() where Y(1) is the four-component column formed by the particle element parameters: i1, i2,
where Y(1) is the four-component column formed by the particle element parameters: i1, i2, ![]() and
and ![]() (1) is the row
(1) is the row ![]() .
.
In this approach the Dirac equations acquire a new interpretation in the momentum space: they have the meaning of covariant relationships connecting the components is and ![]() , parts of the four-component spinor Y:
, parts of the four-component spinor Y:
![]() , (15)
, (15)
where ![]() are spin tensor components expressed in terms of Pm . These relationships correspond to the basic twistor equation in Penrose's twistor program but have an essentially different interpretation. Recall that by Penrose the basic twistor equation characterizes a transition from the momentum variables (momentum and angular moment) to the space-time coordinates.
are spin tensor components expressed in terms of Pm . These relationships correspond to the basic twistor equation in Penrose's twistor program but have an essentially different interpretation. Recall that by Penrose the basic twistor equation characterizes a transition from the momentum variables (momentum and angular moment) to the space-time coordinates.
8. In binary geometrophysics a transition to the space-time coordinates is achieved in another way. It is done using the complexified binary structure of the lowest rank (2,2). Its law can be written in two forms:
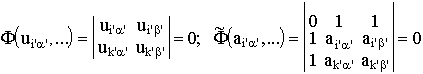 , (16)
, (16)
where the binary relations ![]() and the element parameters are connected by
and the element parameters are connected by
![]() (17)
(17)
9. Given the rank (2,2) complexified binary structure, one can pass to a real unary geometry by matching the elements of the two sets and defining binary relations between the matched element sets, just as it was done for the rank (3,3) structure. It has been shown that this results in a one-dimensional geometry on a directed line. In binary geometrophysics the real binary relations a(1,2) between two matched pairs of elements (i',a') and (k',b') are defined in the form
a(1,2) = ![]() (ai’b‘ + ak'a')
(ai’b‘ + ak'a') ![]() -S(1,2) = S(1) - S(2) (18)
-S(1,2) = S(1) - S(2) (18)
and are interpreted as a classical action between the two particle states.
The two forms (16) of the rank (2,2) structure correspond to the two aspects of particle mechanics, quantum and classical. Recall that in Feynman's formulation of quantum mechanics (Feynman 1948) an elementary amplitude of a transition from one particle state to another is characterized by the quantity
![]() . (19)
. (19)
Thus we can assert that Feynman's formulation of quantum mechanics (path integration) conforms with the spirit of binary geometrophysics.
10. In binary geometrophysics particle momenta Pm and actions S are obtained directly from element parameters of two structures. A transition to a 4-dimensional coordinate space-time is realized by a peculiar composition (multiplication) of two lowest rank ((2,2) and (3,3)) binary structures. It is suggested that the quantities S(1,2) and Pm of the two structures be connected with the invariant relation
![]() , (20)
, (20)
where Dxm are some coefficients to be interpreted as coordinate differences in a four-dimensional pseudo-Euclidean space-time. Since S(1,2) is invariant under transformations (7), Dxm must be transformed as a 4-vector in the Minkowski space. As long as xm appear in (20) in differences, it is an easy matter to understand the origin of the translation group in the coordinate space-time.
Thus one can assert that in binary geometrophysics the coordinate space-time is of secondary nature, being derivable from the more primary concepts of action and momentum. We have shown (Vladimirov and Karnaukhov 1989; Kulakov, Vladimirov and Karnaukhov 1992) the way how the Dirac equations (15) in the momentum space, combined with Feynman's dynamic principle, lead to the free Dirac equation in the coordinate space-time.
11. Physical interactions in binary geometrophysics are derived from the fact that actually the nature is described by higher-rank binary structures than (3,3), just as in multidimensional Kaluza-Klein theories the electromagnetic and other interactions are described by curved space-times with dimensions higher than four. In Kaluza-Klein theories the electromagnetic interaction is described within a 5-dimensional theory and the electroweak interaction can be dealt with in a 6-dimensional theory (Vladimirov 1987). In binary geometrophysics the rank (4,4) degenerate binary structure enables one to construct an algebraic model of electroweak interactions corresponding to the Weinberg-Salam model. The basic algebraic properties of chromodynamics (strong interaction theory) are described by the rank (4,4) non-degenerate binary structure. A transition from binary geometrophysics to the standard theory is accomplished via the Fokker-Feynman direct interparticle action theory.
REFERENCES
FEYNMAN R. (1948). Rev.Mod.Phys. V.20. N.2. P.367.
FOKKER A.D. (1929). Ein invarianter Variationssatz fuer die Bewegung... Z.Phys. Bd.58. Ss.386-393.
KALUZA Th. (1921). Sitzungsber.d.Berl.Akad. S.966.
KULAKOV Yu.I. (1968). Elements of Physical Structure Theory. Novosibirsk (in Russian).
KULAKOV Yu.I. (1971). Doklady AN SSSR. V.201. N.3. P.570 (in Russian).
KULAKOV Yu.I., VLADIMIROV Yu.S. and KARNAUKHOV A.V. (1992). Introduction to the Theory of Physical Structures and Binary Geometrophysics. Moscow (in Russian).
MIKHAILICHENKO G.G. (1972). Doklady AN SSSR. V.206. N.5. P.1056 (in Russian) .
PENROSE R. (1968). Structure of Space-time. N.Y.-Amsterdam.
RUMER Yu.B. (1936). Spinor Analysis. Moscow-Leningrad (in Russian).
VLADIMIROV Yu.S. (1987). Dimensionality of Physical Space-time and Unification of Interactions. Moscow (in Russian).
VLADIMIROV Yu.S. (1988). In: Vychislitel'niye Sistemy (Computer systems). V.125. Pp.42-87. Novosibirsk (in Russian).
VLADIMIROV Yu.S. and KARNAUKHOV A.V. (1989). In: Gravitatsiya I Elektromagnetizm. 4th issue. P.34. Minsk (in Russian).
WHEELER J.A. and FEYNMAN R.P. (1945). Rev.Mod.Phys. V.17. P.157.