© A.Zaslavsky
The concept of an abstract dynamic system’s intrinsic world from the subsystem-observer’s point of view
Alexander Zaslavsky
OBLIK corp., Dnepropetrovsk, Ukraine
This article will be presented as a poster at the conference "Quantum Mind 2003: Consciousness, Quantum Physics and the Brain”, The University of Arizona, Tucson, Arizona.
Correspondence concerning this article should be addressed to Alexander Zaslavsky, OBLIK corp., Dnepropetrovsk 49044, Ukraine, Artema’s str., b.11
E-mail:
![]()
Abstract
The concept of time is proposed and researched. Based on this concept any dynamic system (including the consciousness) is considered in two aspects:
Introduction
Two diametrically opposite approaches to the concept of time are possible:
The first approach conforms to the well-known relational concept of time. In this report time as a system is considered from the point of the second approach.
It is presupposed that the system of time is the relation based on the abstract set being born from causality and consequence unions (Zaslavsky 2002). Their nature is led by the outside world regarding to the system of time. Nevertheless, as we will see further, this relation has not got any determined link with the laws of interaction and movement of subsystems within its own world from the point of its inside observer.
Let us imagine certain creatures (demons) that do not belong to the system we belong. Let us call them conventionally outside and inside demons. In doing so outside demon observes our whole world as a dynamic system from the outside and in his/her time. At the same time the inside demon observes certain dynamic system, which is also comprehensible to our observation, in his own space and time from the inside. The main theses of the time system concept are as follows:
The essence of the initial hypothesis is that unlike the orthodox idea about time, there is a strict linear ordering of events (the absence of simultaneousness as it is) in a system of any nature, be it the system of “our world” or another one. This idea comes as logical consequence of the first and second theses. In fact, if events are linearly ordered and cannot be identified in a space then simultaneous different events cannot be observed. In this case it could be that different simultaneous events may have different points in a space but this is impossible according to the second thesis.
From the first sight such idea seams to contradict our experience. However, who can be confidently that everything in the world surrounding us and we all exist strictly at the same moments of time?
The example of events chain fragment within time system including multiple subsystems and observer himself/herself can be seen in the figure.
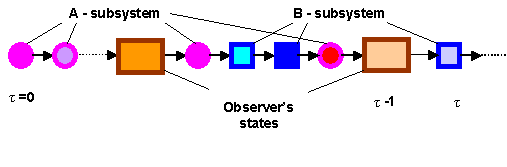
Method
According to the above concept, the informative image of the world to be observed in a given moment of time is determined by the sequence of its states prior to this moment but not by the set of simultaneous events. We can imagine the abstract automation as an observer with the sequence that is coming to its input. The reaction of abstract automation, that is the formation of the next event, is (according to hypothesis) the act of the comprehension of the present. Such automation can have sufficient intellect capable to analyze its past. But from the mathematical point of view, the automation of any degree of complexity is linearly ordered sequence of events.
The question is: how is it possible for the abstract automation–observer that has not having prior knowledge of state measure to reflect its own world within the space?
M. L. Tsetlin (1969) analyzed the reasonable behavior of the abstract automation during its interaction with the random medium and, noted one interesting aspect of this problem. Specifically, in order to maximize some target function of behavior (its winning) such automation must list scores of similar state repetitions (reactions) of the medium being observed by it. So, for the purpose of reaching the reasonability of its own behavior, the observer must distinguish one state from another not only by the quality but by the quantity too, i.e. to score the repetitions of each state of the system under observation.
With the help of this not very difficult procedure the abstract inside observer (subsystem-automation) that is pushed by the necessity to realize the reasonable behavior (in order to survive, for example) finds the measure of states in a form of a ratio of quantities of their repetitions in a chain of events. Whatever method of space and time extent measurements we devise it will always include the recording of state repetitions number of certain system with the help of which measurement is implemented. As far as we can recognize the final quantity of information only, this process must be discrete one i.e. the number of state repetitions must be countable (Harmuth 1989, Zaslavsky 2002).
Results
OWN WORLDS OF THE SYSTEM OF TIME
The main idea of the programme for investigation of own world’s’ laws of the time system is that to derive them as logical consequences from the supposition about strict logical ordering of events chain. With such formulation of a problem it is pointless to put the question about dependence of repetitions frequencies (probabilities) of states in events chain upon dynamic laws of movement and interaction of subsystems within the system of time. On the contrary, it is appropriate to inquire the following: how these laws are determined by the distribution of medium frequencies of repetition of states in the chain of events. Let the system of time during its travel from the event qa (τ) (the idea is that at the moment of time τ it is in a state α) to the event qβ(τ + Δτ) is turned out to be ΔNi times in i-state. This process can be considered as the repetition of i-state ![]() times or as the change of i-state by ΔNi discrete units. Hence,
times or as the change of i-state by ΔNi discrete units. Hence, . In this way, own measure of state change is introduced.
. In this way, own measure of state change is introduced.
![]() , (1)
, (1)
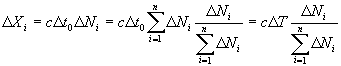 , (2)
, (2)
where X – own vector of state, Т - own time of a system (subsystem) of time, Δtо – quantum of time, c – constant that takes into account relation units of measurement of space extent of states and the time.
Now it is possible to construct arbitrary system of readout, its axes of coordinates correspond to the system states. In this system of readout projections of small movements (![]() ) of representative point are connected with corresponding small changes of own vector of state by linear expressions of general view
) of representative point are connected with corresponding small changes of own vector of state by linear expressions of general view
 , (3)
, (3)
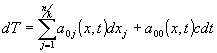 , (4)
, (4)
where x – state vector in an arbitrary system of readout, ![]() - conversion coefficients of an arbitrary system of readout in own system, t - time in an arbitrary system of readout.
- conversion coefficients of an arbitrary system of readout in own system, t - time in an arbitrary system of readout.
Space dimensionality equals the number of classes of the system states n. If we will study the system not as a whole but as an ensemble of k-subsystems, each of them is turned out to be one of n/k states (set of states intersections is empty), then the system is represented by points k in space of n/k dimensions. Let us emphasize that the representation of time system evolution with points and their trajectories in a space of states is the abstraction convenient for perception only. In reality, there are no points and trajectories in space because in each moment of time the system is turned out to be in one state only (only one coordinate has got defined value). But if on the small enough lengths of time the observer is able to distinguish separate events but is not able to distinguish their sequence within the time, then state changes for him/her will occur as if they are simultaneous ones. In this case, he/she needs the idea of multi-dimensional space as a receptacle of these simultaneous changes. The absence of ability to distinguish the order of events that are close enough in time, is typical for the level of prototemporal perception (Fraser 1972). For example, based on capabilities of people’s sensations, periods of 20-50 ms duration can accommodate events that possible to count but people cannot these events in any time order.
The very relevant disparity is received from the formula (2) testifying about the limitation of the rate of state change in the system of time.
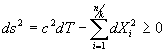 . (5)
. (5)
This disparity can be converted to an invariant kind (valid in an arbitrary system of readout), substituting in it of value variable, taken from the formulas (3,4).
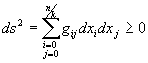 , (6)
, (6)
where is indicated ![]() ,
,
![]()
![]() . (7)
. (7)
An invariance of an interval ds to a transformation aij(x,t) of coordinates of space and time follows from the formulas (1,2,5).
Analysis of the dependence of events chain number having different order of states running upon the length of events chain resulted in the second fundamental inequality testifying the increase of accumulated entropy within the system of time.
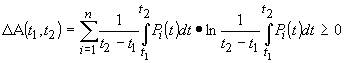 , (8)
, (8)
where Pi = ![]() – probability of i-state on so small period of time that the order of states running is imperceptible for the observer; ΔA(t1,t2) – the change of accumulated entropy of events chain.
– probability of i-state on so small period of time that the order of states running is imperceptible for the observer; ΔA(t1,t2) – the change of accumulated entropy of events chain.
THE PRINCIPLE OF THE MOST PROBABLE CHAIN OF EVENTS
Let us watch the movement and interaction of subsystems in the most probable chain of events. For this purpose we take into account the limitation of the rate of states change (pl. ref. before) and additions of probabilities normalization. Let us express state change frequencies in the chain of events via the increment of coordinates of its own space. Therefore, we reach the variation problem of the analysis of conditional extremum of entropy growth because the last is proportional to logarithm of events chain probability.
 (9)
(9)
where 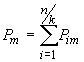 – probability of states of m-subsystem,
– probability of states of m-subsystem, ![]() – invariant time-space interval.
– invariant time-space interval.
Here values
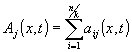 (10)
(10)
play the same part as components of vector potential in a theory of electromagnetic interactions. The solution of this problem is the application of equations that are analogous by the form to equations describing the interaction of electrically charged particles in our world.
The joint set of equations (7) and (10) indicates existence of intercoupling of electromagnetic and gravitational fields in an own world of a system of time.
Label by  the medium probability of events chain. Note the normalization of probabilities. Place energy levels Ei in correspondence with the states of the system. Try to keep the average energy U of the system unchangeable.
the medium probability of events chain. Note the normalization of probabilities. Place energy levels Ei in correspondence with the states of the system. Try to keep the average energy U of the system unchangeable.
Examine this problem
 (11)
(11)
When solving this problem we get equations that underlie thermodynamics (Haken, 1978). But unlike derivation of the above equations that was suggested by Haken (1978), our derivation is true with regard to any thermodynamic processes including irreversible ones that are far away from the state of thermodynamic equilibrium.
It works due to the fact that in the most probable chain of events the maximum of accumulated entropy is gained during the time interval ![]() irrespective the maximum degree of uniformity of probabilities Pi distribution that is reached in the state of thermodynamic uniformity only.
irrespective the maximum degree of uniformity of probabilities Pi distribution that is reached in the state of thermodynamic uniformity only.
Discussion
It is important to emphasize that in the present paper the laws of state change and interaction of subsystems in the own world of the abstract system of time were derived without the use of empiric generalizations. Moreover, these laws happened to be analogous in form to well-known physical laws of our world. Therefore, the most probable of these laws have occurred due to linear ordering of events and due to the method of system states measured by its inside observer (as previously discussed in this paper).
The model of consciousness from the position of the theory of psychophysical identity (Ivanov, 1998) can be given in a form of time system including outside and inside observers. In doing so an outside observer comprehends its evolution as a chain of random events subjected to the influence of outside world and inside observer as determined movement and interaction of subsystems within his own world. It is important to emphasize that the nature of subsystems movement in the own space of the system does not depend on the order of states running within the chain of events. It is defined by the distribution of relative number of repetitions of similar states only. As far as this distribution in the most probable chain of events, at least, meets the determined laws then random distribution of states matches the determined movement of subsystems in its own world.
Maybe it is here that we shall look for the bridge between the spontaneousness of wave function reduction in quantum model of consciousness (Hameroff, Penrose, 1996) and the determinacy of the observer’s perceptions of his/her own world? Maybe it is here that we shall look for the bridge between the determinacy of reasons that produce the system of time and inside observer’s free will in its own world?
References
Fraser, J.T. (1972), The study of time. I:, New-York: Springer-Verlag,- 479pp.
Haken, H. (1978), Synergetics, Springer-Verlag Berlin Heidelberg New-York, -404pp.
Hameroff, S., Penrose, R. (1996), Orchestrated Reduction of Quantum Coherence in Brain Microtubules : A Model of Consciousness // Toward a Science of Consciousness. The First Tucson Discussions and Debates. Tucson.
Harmuth, H. (1989), Information Theory Applied to Space - Time Physics, M.: “Mir”,- 342pp, (in Russian).
Ivanov, E. M. (1998), Matter and subjectivity, Saratov State University, -168pp, (in Russian).
Tsetlin, M. L. (1969), Researches on automata theory and simulation of biological systems, M.: “Nauka”, - 316pp, (in Russian).
Zaslavzky, A. M. (2002), Metaphysics and system analysis, Institute of researches of the nature of time, (in Russian).