STARS AND KOLTSARS1
V. E. Zhvirblis
1. Introduction. Time as hidden variable
The basic publication of N.A.Kozyrev (1958) devoted to the time phenomenon touched upon two fundamental problems that often attracted attention of the physicists, have only recently been considered methodically and thoroughly. The first problem concerns the occurrence of macroscopic irreversibility in systems that are microscopically reversible by definition. The second one, which is usually not related to irreversibility, is the problem of quantum nonlocality and hidden variables.
Two preceding publications of Kozyrev that present his original ideas under respectable disguise allow one to understand the hidden logic of appearance of the heretic “causal” or “nonsymmetrical” mechanics. Relying upon numerous astrophysical observations, he called in question the then generally accepted thermonuclear hypothesis of star energy origin (Kozyrev 1948, 1951). As followed from these publications, the Sun and the stars were to be considered not as isolated systems tending during evolution to thermodynamic equilibrium, but rather as open systems exchanging energy with the environment and capable of self-organization, that is, as somewhat similar to the living organisms. (It might be well to make a parenthetic remark that by the end of 1940s the thermodynamics as a science describing vital activity, evolution, and self-organization did not exist at all.)
Kozyrev approached the problem of irreversibility in a very original manner. Beginning from L.Boltzmann, vain attempts were made to derive irreversibility of thermodynamics from reversibility of mechanics, preserving simultaneously determinism (statistical distribution is a rather strong hypothesis). Kozyrev assumed that irreversibility by itself is the fundamental property of any real system (which is the only subject of the thermodynamics if it claims to describe correctly the observable natural phenomena) and that reversibility occurs only if (as happens with the classical mechanics dealing with speculative models) interaction is disregarded of these systems with the flow of a special substance that defines objectively the direction of “time arrow,” penetrates all at once the Universe, and, therefore, can cause what today would be called nonlocality effects. (Note also that the Bell theorem relating nonlocality and determinism dates back only to the mid-1960s.)
Kozyrev called this substance “time” causing much terminological misunderstanding. Had he called this substance “physical vacuum”2, there would have been no problem, but by the middle of this century the quantum electrodynamics was only in the making. If so, the Kozyrev “causal” or “nonsymmetrical” mechanics should be ranked with the theories of hidden variables.
If interpreted in this way, the Kozyrev’s research turns out to lie (by its essence, not form) along the mainstream of the ideas of modern thermodynamics of irreversible processes that deals exactly with manifestations of nonlocality (Prigogine, Stengers 1984). If the stars are nonlocal natural objects existing at the expense of physical vacuum energy, one cannot exclude the plausibility of artificial objects that feature the same properties and can be studied in the laboratory environment. In doing so, one has to take into consideration that the observed effects must be extremely small and look as impossible at their superficial consideration, that is, from the standpoint of the classical equilibrium thermodynamics.
2. Lazarev’s koltsar
2.1. Phenomenology
As was shown earlier (Zhvilblis 1991, 1993), the observed by M.F. Lazarev continuous circulation of volatile liquid in closed ring-shaped vessel with porous partition (the so-called “koltsar,” from Russian “koltso” — ring), which formally looks like continuous current circulation in a superconductive ring, is not an experimental artefact, but rather a direct consequence of the difference between any real thermodynamic system (that is, system with nonequilibrium metastable structure) and the ideal structureless systems considered by the classical thermodynamics and maintained in a state close to that of true thermodynamic equilibrium.
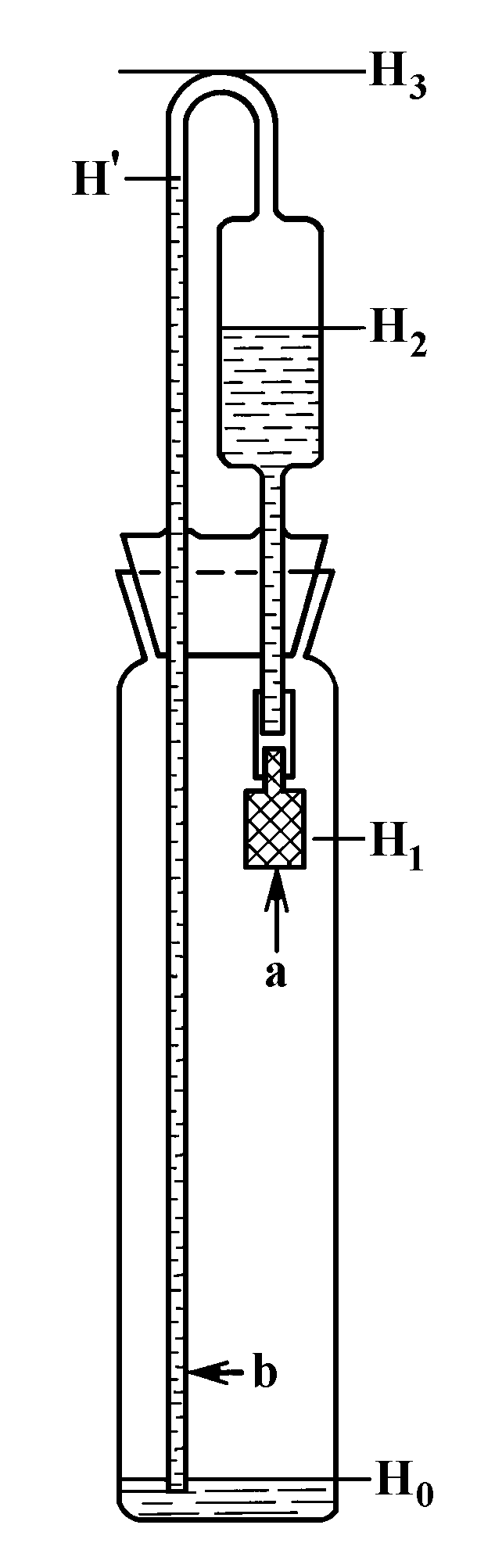
One of the most informative experiments by Lazarev was as follows. Some amount of water was placed into the upper part of a closed ring-shaped vessel with a porous partition (Fig.1), and dynamics of water rise in the bypass pipe was observed during a long interval (up to four years).
Simple calculations show that owing to the surface tension forces existing in the capillaries of porous partition, the liquid in the bypass pipe must rise not to the level H2-H1, but rather to the level
![]() ,
,
where s is the surface tension, q is the boundary angle, r is the liquid density, r is the radius of porous partition capillaries, and g is the free fall acceleration. It is natural to imply here that the system is maintained in strictly isothermic conditions and is completely isolated from the environment.
It is precisely this additional rise of liquid due to the capillary pressure forces that was observed by Lazarev (Fig.2). It is in good agreement with the quantitative estimates. Three distinct parts of the process can be identified in the figure: fast attainment of the hydrostatic pressure balance (break at the level H2-H1), much slower rise of the liquid level in the bypass due to the capillary pressure forces until the balance of all forces (break at the level Hў ), and, finally, long quasi-stationary stage where no changes are observed in the system.
It is, thus, obvious that the level of water (or any other liquid) in the bypass can be steadily over that above the porous partition, provided that the following simple condition is satisfied:
![]() , (1)
, (1)
which is the case in the above experiment. It is also evident that the quasi-stationary stage cannot last arbitrarily long, because it is a basically nonequilibrium system, and the liquid above the porous partition must move down eventually. The problem is only in what manner and how soon this will happen.
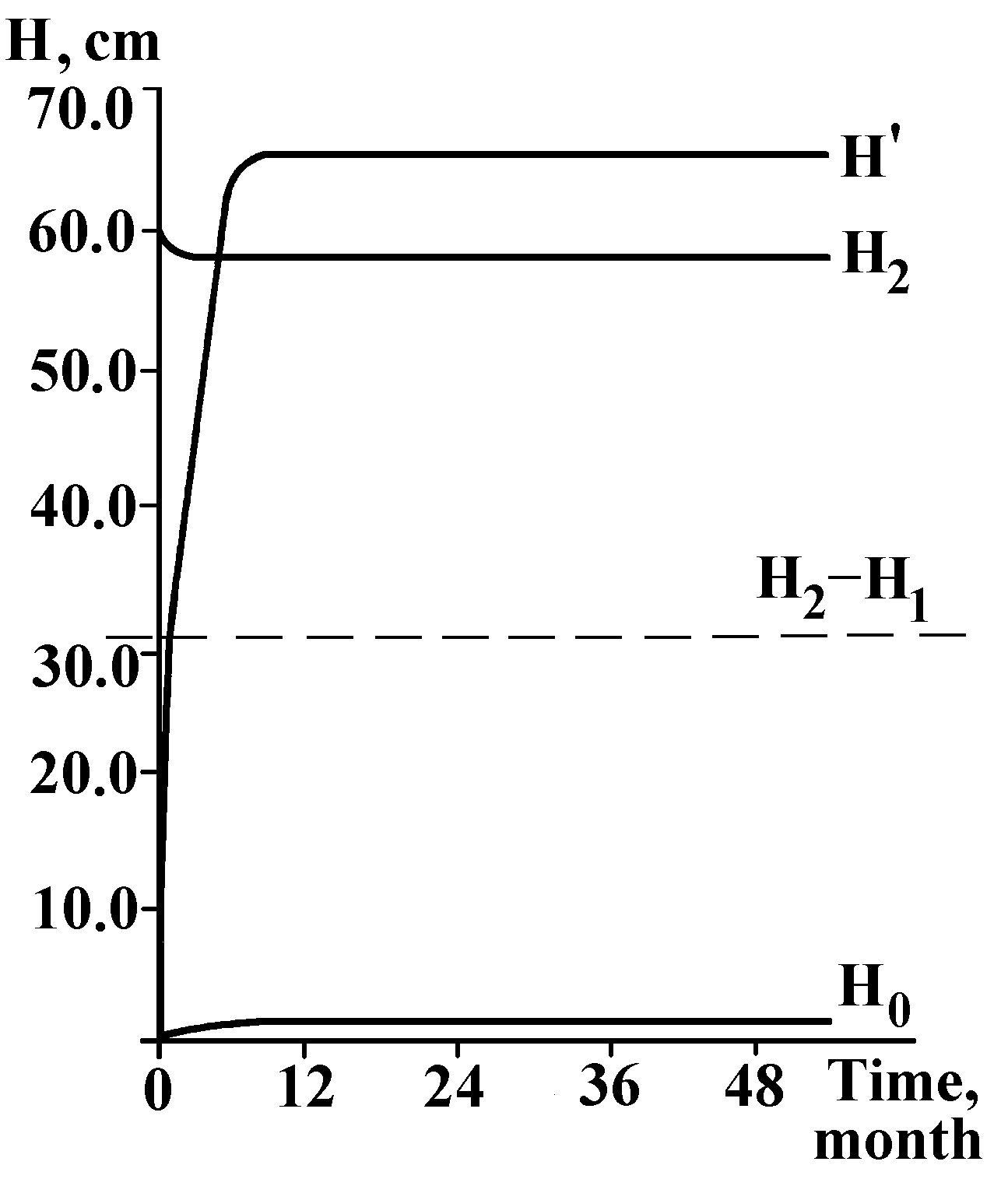
Fig.1. Diagram of the Lazarev’s koltsar: a — porous partition; b — bypass pipe.
Fig.2. Results of one Lazarev’s experiment. Liquid — water; porous partition made of chamotte; H3 ~ 70cm > Hў .
It seems that we deal with an extremely slow process, because Lazarev observed no noticeable change in the level Hў during four years. This could be isothermic recondensation occurring because of the difference of pressures of saturated liquid vapor in the gravity field at the level H0 regarded conventionally as zero level, and at the level H1 near the surface of porous partition.
If the saturated vapor pressure immediately over the liquid surface is P0, at the height H its pressure PH is defined by the so-called barometric formula
![]() ,
,
where m is the liquid molecule mass, k is the Boltzmann constant, and T is the absolute temperature. That is why in the setup of Fig.1 the liquid will evaporate spontaneously from the porous partition surface and condensate on the vessel bottom. Because the levels H2 and Hў go down very slowly, the following difference between them being steadily preserved:
![]() .
.
When no liquid at all is left above the porous partition and nothing handicaps pressure equalization, the bypass level will drop quickly to ![]() and the system will pass into the equilibrium (or, more accurately, conditionally equilibrium) state. This process that seems to require many decades for realization is depicted in Fig.3.
and the system will pass into the equilibrium (or, more accurately, conditionally equilibrium) state. This process that seems to require many decades for realization is depicted in Fig.3.
2.2. Circulation mode paradox
The rise of liquid in the bypass to the level Hў >H2 is, therefore, a trivial phenomenon readily explainable by the elementary physical laws and observable experimentally. It is not yet an engineering challenge to create conditions where koltsar’s behavior becomes puzzling. Namely, if
H3 < Hў , (2)
the liquid can return spontaneously by natural course from the bypass into the space over the porous partition, thus resulting in substance circulation, the passage to the conditionally (we stress it again!) equilibrium state becoming practically impossible if s , q , r , g and r that define additional liquid rise in the bypass, and also the vessel size are constants. It turns out that, although these variables are not defined by the conservation laws, it is their relation that defines koltsar’s ability either to pass into the equilibrium state, or to be indefinitely long in the mode that is not envisioned by the equilibrium thermodynamics (Fig.4).
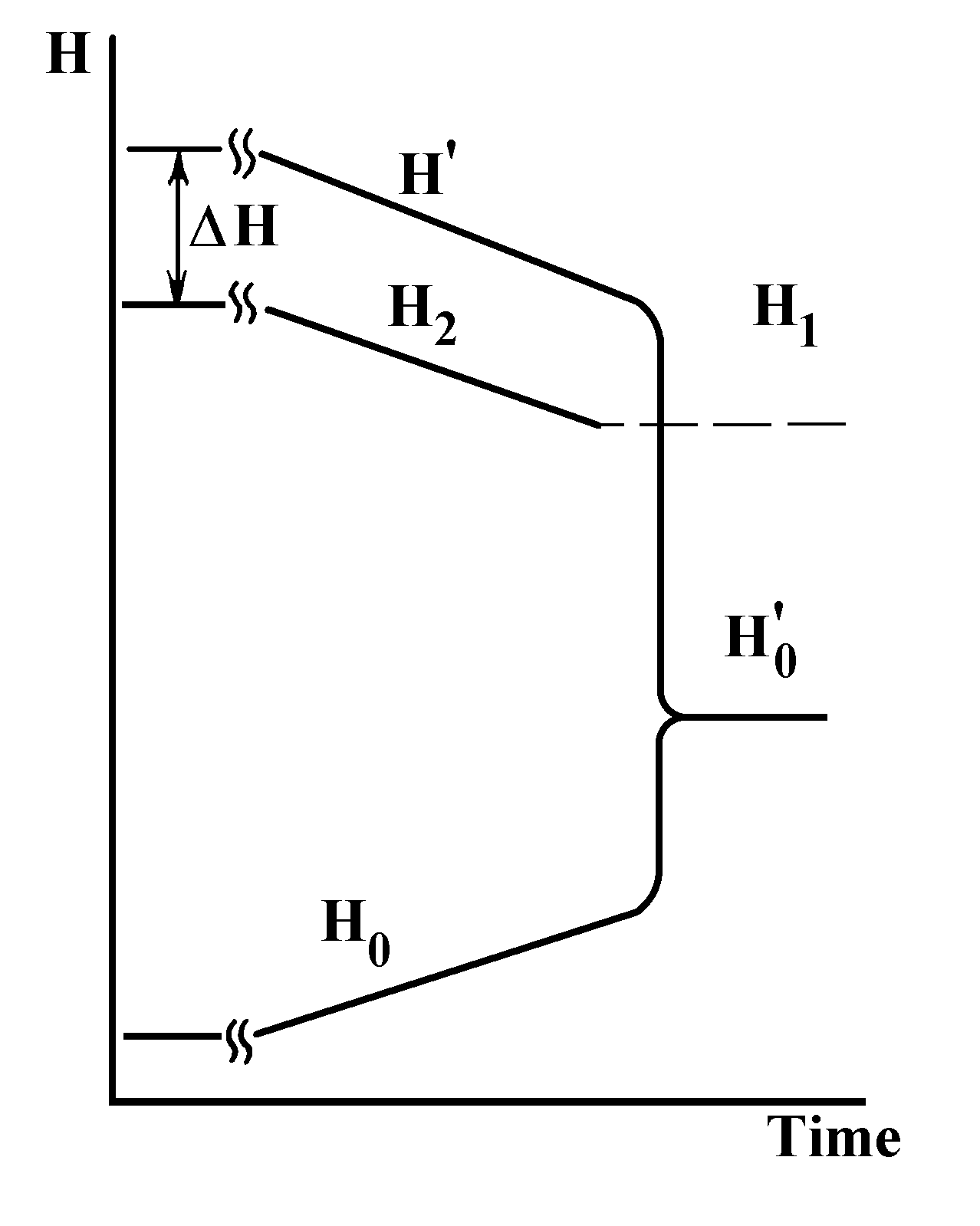
Fig.3. Diagram of koltsar transition into the equilibrium state as a result of isothermic recondensation.
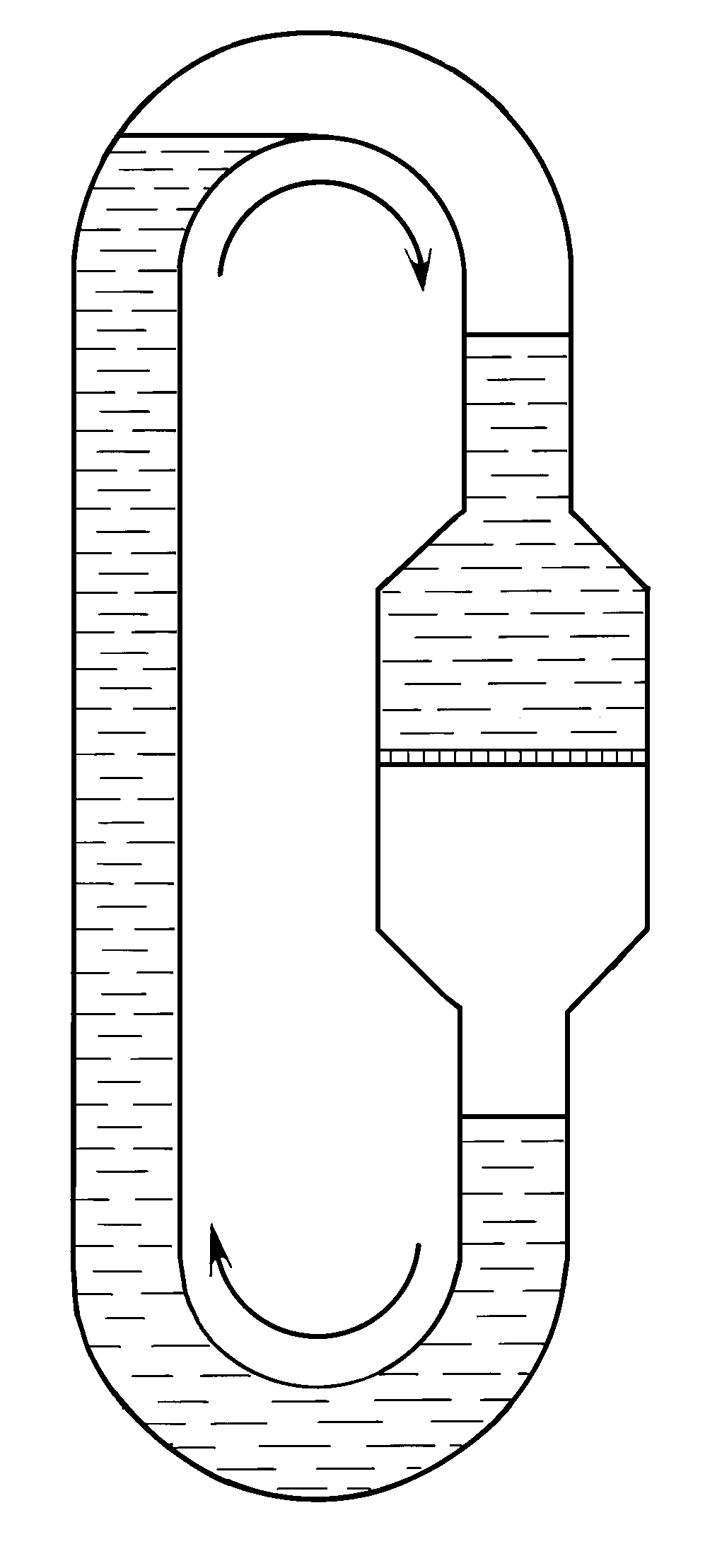
Fig.4. Circulation of liquid in the Lazarev’s koltsar under H3<Hў .
Also, it can be shown that the system passage to the equilibrium state, as shown in Fig.3, should not at all occur if the condition (1) is satisfied and (2), is not. The point is that in addition to the isothermic liquid recondensation between the porous partition surface and the vessel bottom, the same process must occur between the liquid surface in the bypass at the height Hў and the liquid above the porous partition at the height H2. If the velocities of these processes are equal (they depend not only on the saturated vapor pressure, but also on the area of free liquid surface defined arbitrarily by the vessel dimensions), circulation may go on indefinitely long.
The paradoxical behavior of the Lazarev koltsar becomes even more evident if one takes into consideration that evaporation and condensation are accompanied by thermal effects. This means that in a system that is isothermic by definition, spontaneous stationary temperature difference must occur, that is, a phenomenon must be observed that can be formally interpreted as an obvious violation of the second principle of thermodynamics.
This thermodynamic paradox looks so unusual because of its discouraging simplicity and obviousness — it seems as if solvable if one either sacrifices the elementary physics and denies the existence of elementary phenomenon (capillary pressure), or repudiates the classical thermodynamics and confesses realizability of the second-kind perpetuum mobile. Such dichotomy is erroneous in principle, because the problem is not in revising the natural laws, but in determining correctly their domain of application.
Indeed, the classical physics is incapable of accounting for the quantum phenomena such as superconductivity, to which the thermodynamic laws are not applied, whereas the classical thermodynamics failed to explain the phenomenon of life that turns out to be explainable in terms of the thermodynamics of irreversible processes3. The Lazarev paradox, therefore, could be easily solved by recognizing the koltsar either as a quantum system, or as living nonbiological structure existing at the expense of energy exchange with the environment. Still, even these quite plausible hypotheses seem like too strong for the today scientific mentality. Instead of stimulating the search of a reasonable answer, the effect of koltsar causes an absolutely irrational, purely defensive psychological response of ignoring stubbornly both the problem and the experimental facts underlying it.
2.3. Nonquantum bistable systems
The ability of quantum systems to be simultaneously in two different stationary states, that is, to exist as certain metastable dynamic structures, is one of their distinguishing features. The only electron in the molecular hydrogen ion H2+ cannot be coupled to only one of the two identical protons, but is in constant motion trying to belong to both. As a result, besides the usual Coulomb repulsion force, the so-called exchange interaction force appears making the system stable, because the particles are in the potential wells. At low temperatures, the same exchange-type interaction forces relating the electrons into the Cooper pairs are responsible for the phenomenon of superconductivity taking place near the absolute zero. The superconductive ring where current can circulate arbitrarily long can also be called koltsar in a sense, because by appearance it does not fit the scope of phenomena tolerated by the classical thermodynamics.
The reasons why the well-known quantum effects such as superfluidity and tunnelling, to say nothing about superconductivity, are not regarded from the standpoint of thermodynamics are more of historical than scientific nature and are not related directly to adequate description of physical reality. Namely, these effects were first discovered experimentally and only then explained theoretically, which required the quantum mechanical concepts that differ from those of the classical mechanics at the axiomatic and even preaxiomatic level and just ignore the very existence of the second principle of thermodynamics. All the real world objects were classified accordingly into two groups — classical and quantum, although this division is obviously conventional and concerns the means of description rather than the objects themselves. Therefore, the fact that the koltsar effect is observed and described at the macroscopic level, but is not explained theoretically ab ovo, that is by the traditional theories, and systems of postulates and preaxiomatic notions, whereas superconductivity and other quantum effects are observed and accounted for even at the macroscopic level, does not imply at all that there exists no such effect and/or that there can be no rational explanation of it.
Application of the second principle of thermodynamics to the real world systems is known to require great care. It provides reasonable results only if the very notion of “system” is defined strictly. In strongly nonequilibrium systems, circulation-like phenomena are possible. The only question is their duration. If the system is isolated, circulation duration will be defined by the free energy margin and process kinetics that can be hampered significantly, especially at low temperatures, by high potential barriers. If the system is open, circulation duration will depend on the free energy margin of the environment that can be extremely great and, at the limit, infinite. If one is afraid of not knowing something about the system characteristics and the circulation causes, the koltsar enables one to judge about them by the results of observations.
Besides the observed circulation of substance particles (electrons or molecules) that is not accompanied by noticeable dissipative processes, do the superconductive ring and the Lazarev koltsar have some other features in common? First and foremost, both are obviously very distant from thermodynamic equilibrium, if for no other reason than that they feature quite certain structure and are metastable in principle. Therefore, applicability of the reversible thermodynamics laws to them seems questionable. In both systems, circulation is due to two different forces of physical interaction, that is, to forces having different physical nature — these are Coulomb interaction and exchange forces in the case of superconductive ring, and gravitational and intermolecular interaction forces in the case of Lazarev koltsar. Joint action of two forces gives rise to two different stationary states that are directly responsible for circulation.
Thus, the quantum and nonquantum systems are phenomenologically very similar from the point of view of thermodynamics, the difference is only in the interpretation of this similarity — what is to be regarded as cause, and what, as effect. For instance, in the quantum system the exchange interaction forces are considered as the effect of two stationary states, which is postulated initially; whereas in the nonquantum system it is the forces given as physical reality that are the cause of two stationary states.
Therefore, one can assume that any (and not only quantum) nonequilibrium physical system where two stationary states can be discovered theoretically and/or experimentally, must behave like the Lazarev koltsar.
3. Osmotic koltsar
3.1. Solution of the paradox
In the Lazarev koltsar, one stationary state is due to the system’s trend to equal pressure of saturated vapor over the liquid in the bypass and above the porous partition (it is attainable for Hў = H2), and another, to the trend to equal hydrostatic pressures produced by the liquid columns from the left and the right (attainable for Hў =H2-H1). Because both conditions cannot be satisfied simultaneously, circulation occurs in the koltsar that is terminated or does not occur at all in two cases: if H1=0 (the surface tension forces do not act), or if Hў =0 (there is no gravity force). The problem, therefore, is how the koltsar can pass into the equilibrium state.
The Lazarev koltsar is of interest because it allows us to observe experimentally the circulation effect and explain its mechanism. Yet as a model for quantitative evaluations it is inconvenient. Such a model can be obtained by using a koltsar where two states occur because of osmosis.
If in a ring-shaped closed vessel with semipenetrable partition one places on one side pure solvent (e.g., water), and on the other side, solution of some nonpenetrative substance such as saccharose, according to the Van’t Hoff equation for ideal solutions, the following osmotic pressure will act from the solvent to the solution:
![]() ,
,
where ![]() is the actual solute concentration near the semipenetrable partition, R is the gasconstant, and T is the absolute temperature. The system hydrostatic equilibrium condition is as follows:
is the actual solute concentration near the semipenetrable partition, R is the gasconstant, and T is the absolute temperature. The system hydrostatic equilibrium condition is as follows:
![]() , (3)
, (3)
where ![]() is the mean solution density, r 2 is the solvent density, g is the free fall acceleration, H is the solution level, and h is the solvent level (Fig.5).
is the mean solution density, r 2 is the solvent density, g is the free fall acceleration, H is the solution level, and h is the solvent level (Fig.5).
In the equilibrium isothermic environment, the solute concentration varies with height under the action of the gravity force. At the zero level, near the semipenetrable partition it will be
![]() (4)
(4)
and at height H
![]() , (5)
, (5)
where r 1 is the solute density, m1 and M1 are its mass and molecular weight, and m2 is the mass of solvent in the solution. The mean solution density is as follows:
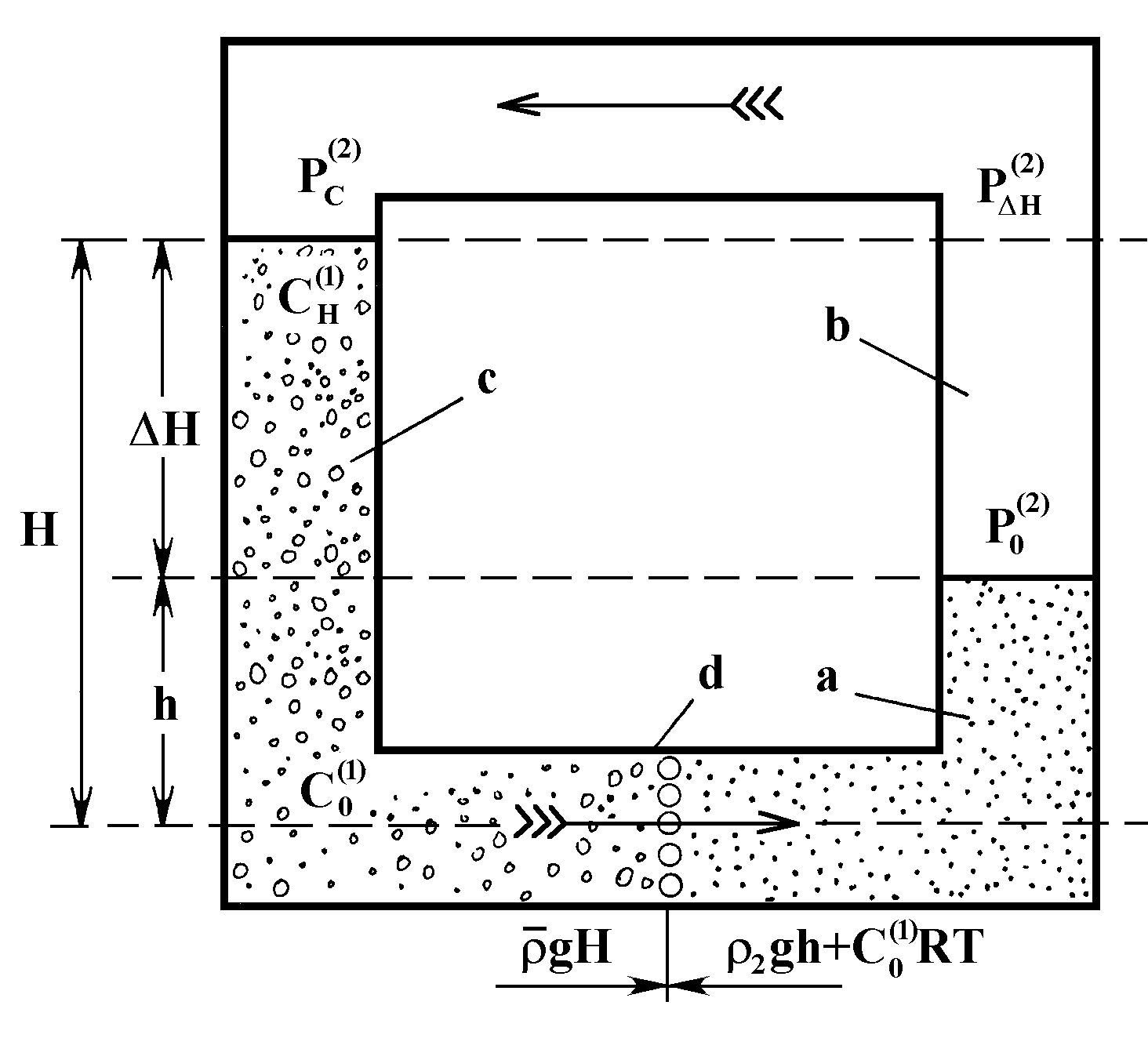
![]() . (6)
. (6)
Fig.5. Diagram of osmotic koltsar: a — solvent, b — saturated vapor, c — solution, d — semipenetrable partition.
By substituting (4) and (6) into (3), we obtain that
![]()
![]() .
.
If the saturated vapor pressure above the pure solvent is ![]() , at height H it will be
, at height H it will be
![]()
with M2 for the solvent molecular weight. The pressure immediately above the solution with concentration ![]() as defined by (5) will be in compliance with the Raoult law as follows:
as defined by (5) will be in compliance with the Raoult law as follows:
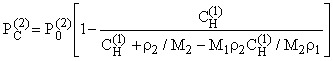 .
.
As a result, one can determine
![]()
as the function of C, H and T. Its analytical form of this function is extremely cumbersome. Therefore, using on the reference sources, calculations were carried out for saccharose water solutions with concentrations 1.5% and 15% (it was assumed that at 288K, r 1 = 1.558g/cm3 and ![]() = 12.788mm Hg). Their results are plotted in Figs.6 and 74.
= 12.788mm Hg). Their results are plotted in Figs.6 and 74.
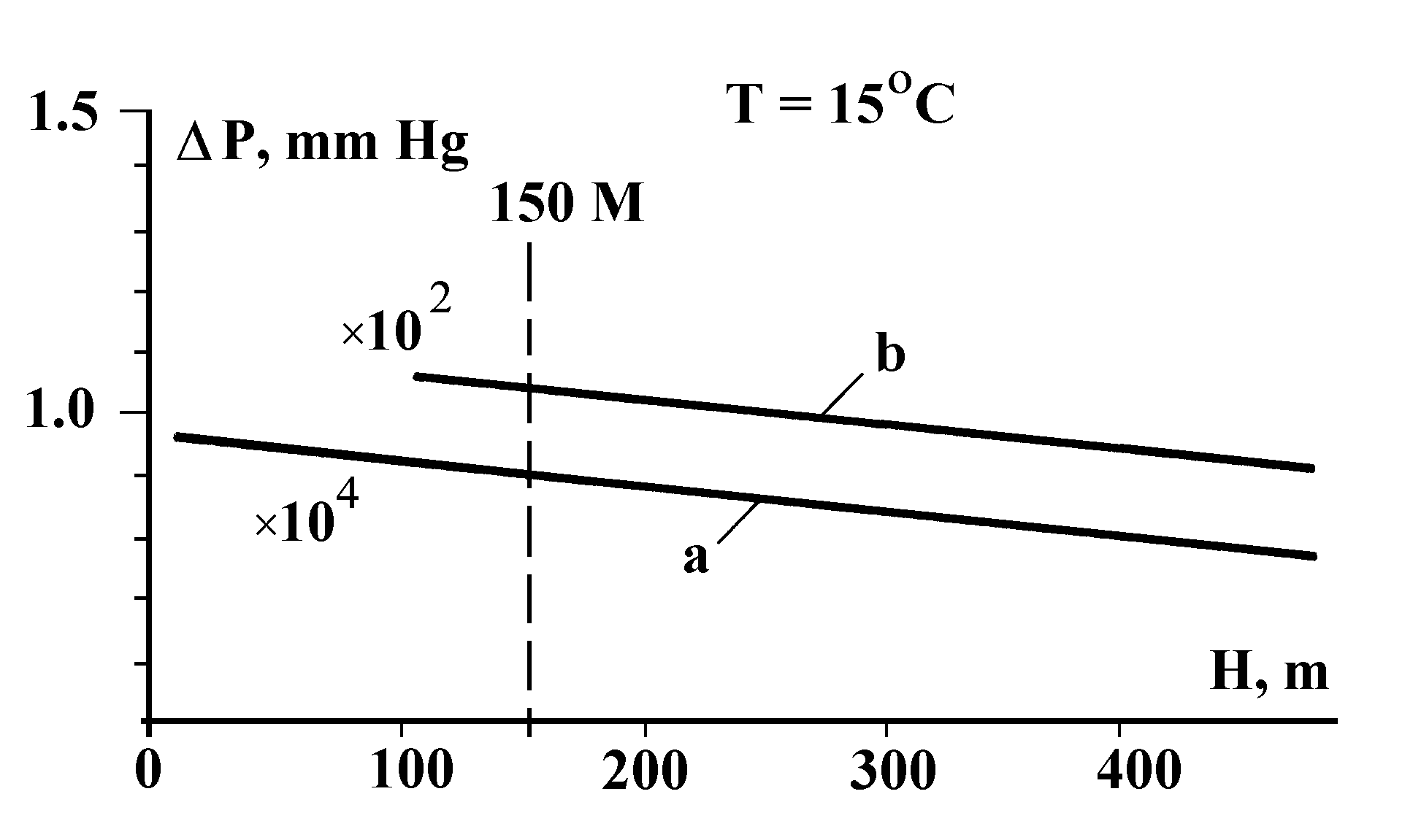
Fig.6. D P vs. size of osmotic koltsar: a — for 1.5% solution of saccharose, b — for 15% solution of saccharose (at 15° C).
The obtained dependencies of D P on solution concentration, koltsar size and temperature lead to several fundamental conclusions.
1. If D P № 0, there should be solvent circulation in the system (in the direction shown by the arrows in Fig.5) similar to circulation in the Lazarev koltsar.
2. Solvent circulation is terminated only if at least one of the following conditions is satisfied: C® 0, H® Ґ , T® 0K. Stated differently, circulation is impossible only in the true ideal system, that is, infinite-dimensional system with infinitely diluted solution at the temperature of absolute zero.
3. The fact that the Van’t Hoff equation and the Raoult law are inapplicable to the real solutions has no effect on the essence of the matter — a precisely “correct” result (D P=0) has been obtained for the ideal solution, and any correction could only lead to “incorrect” result (D P№ 0) even under the conditions C® 0, H® Ґ , T® 0K. The fact that circulation is impossible below the solvent freezing temperature and above its critical point, also does not change the heart of the matter, but rather confines the effect feasibility domain to the liquid phase existence domain.
Fig.7. D P vs. system temperature: a — for 1.5% solution of saccharose, b — for 15% solution of saccharose (koltsar height 150 m).
4. Like with the Lazarev koltsar, the effect occurs because the osmotic koltsar belongs to the class of bistable systems where one state is defined by the condition (3), and another, by the requirement of equal pressures of saturated vapor at height H above the solution and pure solvent.
5. Like the Lazarev koltsar, the osmotic koltsar is a system initially far from the thermodynamic equilibrium, because the semipenetrable partition prevents mixing of the solution and pure solvent and solute volatility practically can be zero. Also, no matter how large solute molecular weight is (e.g., it may be a protein with molecules of much larger size than the diameter of partition pores), there is always a theoretical nonzero possibility that the solute will penetrate through the partition and evaporate from the solution (this process may be enhanced by spontaneous destruction of solute molecules as well as of the partition material, that is, by system ageing). In other words, the deviation of D P from zero is the result of kinetic difficulties, that is, of the existence of finite-height potential barriers. Also, the stronger the difficulties, the longer is koltsar “lifetime”5.
Therefore, although koltsar lifetime is theoretically limited by its nonequilibrium, metastable state (i.e., its existence as a certain structure), it can practically be arbitrarily long and comparable, for example, with that of the Universe. This is the solution of the koltsar paradox (as of the thermodynamic aspect of superconductivity) — the laws of the classical thermodynamics are applicable only to the ideal systems, whereas the koltsar (as the quantum object) is a system whose behavior can be described correctly only by the irreversible process thermodynamics that was created primarily for accounting for the phenomena of life and biological evolution.
3.2. “Demon” of koltsar
The semipenetrable partition screening molecules by size performs in essence the same functions as the Maxwell demon sorting molecules by velocities. And if such a device exists in real fact, one should specify its relation to the laws of thermodynamics.
If the demon had worked, that is, shifted thermodynamic equilibrium and, in doing so, consumed no free energy, we would have dealt with violation of the second principle of thermodynamics. If the demon had worked and consumed free energy obtained from nowhere, we would have dealt with violation of the first principle of thermodynamics. But if the demon works and, in doing so, consumes free energy from certain source and produces entropy, no thermodynamic law is violated. The problem is in determining where is the energy source — inside or outside the system under consideration. In the first case, demon’s work will be accompanied by inevitable degradation of the system, its ageing protracted for some time; in the second case, the demon can work indefinitely long without any internal changes in the system, because it is the environment that will degrade.
Because, according to Lazarev, the liquid in koltsar not only may circulate but must also do so by virtue of the two different stationary states existing in this and other similar structures, and because we have no ground to question the validity of the laws of thermodynamics, the quest for the effect cause should be aimed at the source of demon’s energy.
First of all, attention is drawn to the fact that the free energy activating koltsar is of explicitly nontrivial nature because it does not appear at all in the Van’t Hoff and Raoult laws from which circulation feasibility follows6, but appears rather as some phantom. In this connection, it remains to assume that some physical reality appears implicitly in these simple laws at some preaxiomatic level, that is, as something that goes without saying. Indeed, circulation in koltsars appears not because of attaining the equilibrium state, but because of two different stationary states appearing by virtue of physical interaction forces. The origin of these forces is not considered at all, their existence being accepted as a perfectly obvious physical reality.
Further, the kinetic energy of solvent molecules circulating in the closed loop of osmotic koltsar can be transformed obviously into useful work (e.g., by placing across the vapor flow a turbine lifting a weight). The total system energy will still remain constant — as the weight is lifted, the temperature of koltsar, which can be regarded as being strictly isolated from the usual thermodynamic contacts with the environment, drops until the process is terminated spontaneously at 0K. Now, the potential energy stored by the weight can again be transformed into heat that will warm up the koltsar precisely to the initial temperature. It seems that isothermic transformation of heat into useful work and vice versa can be repeated as often as desired (at least, as long as the koltsar exists as metastable structure). It turns out that the problem of irreversibility is a false one — reversibility of thermodynamics is inferred from reversibility of mechanics as applied to koltsar as metastable structures! Correspondingly, irreversibility of thermodynamics can be inferred from mechanics only if the latter is postulated to be irreversible, which is what Kozyrev did.
Therefore, no matter how hard we try to isolate the koltsar from the usual thermodynamic contacts with the environment, it remains a basically open system to which high- potential energy is delivered continuously and from which low-potential energy is removed. This energy flow supporting koltsar and other metastable structures (i.e., any material objects in essence) in the stationary nonequilibrium state is most probably of cosmophysical nature as witnessed not only by most general considerations, but also by appreciable relation between power fluctuations in the Lazarev koltsar and variation of Sun activity.
It is precisely in this cosmophysical context that one can solve the problems of Maxwell demon as a special device supporting contacts between all bodies in the Universe and manifesting itself in nonlocality effects like macroscopic fluctuations observed in systems of different natures (Udal’tsova, Kolombet, Shnol’ 1987; Vladimirsky 1990), or Sun activity rhythm defined by the motions of the solar system planets, or solar-terrestrial relationships (Miroshnichenko 1981).
3.3. Kinetic attributes of two states
Detection of liquid circulation in closed loop cannot by itself provide a reliable proof of koltsar effect, because one cannot find in this manner how long circulation will go on, if it is not just a trivial transient process, or if it is not caused by a trivial external action. Such a proof can be provided by establishing that the system can be in two different stationary states, because here one can assert with full confidence that circulation must occur inevitably and can go on arbitrarily long, that is, as long as the koltsar exists as a certain physical structure.
In the osmotic and Lazarev koltsars, one state is due to system’s trend to equalize the pressures created by liquid columns in the communicating vessels, and another, to the condition of equal pressures of the saturated vapor over the liquid in the right and the left parts of the vessel. To bring the system into one of these states, one has to break the osmotic koltsar loop either from below, or from above and allow the system to reach dynamic equilibrium where the velocities of solvent molecules (in the liquid phase or in the vapor) become equal from the right to the left and from the left to the right.
If, then, one again closes the koltsar loop and records the direction and velocity of solvent mass transfer, it will be seen that to each of the two different system states its characteristic kinetics corresponds. Namely, in one case smooth enter of the mass transfer velocity into the plateau must be observed, whereas in another case this enter must be preceded by a change of mass transfer direction (Fig.8). Since the liquid has inertia and experiences viscous friction, and since the partition resists significantly its motion, at the beginning of circulation mode in the koltsar there should be mass transfer oscillations with period and decay time characteristic of each particular system.
Detection of two such kinetics provides an irrefutable proof of the existence of two different stationary states in the system. As a result, liquid circulation is the only possible form of stable state of the system much as continuous motion is the only possible form of stability of the system of celestial bodies.
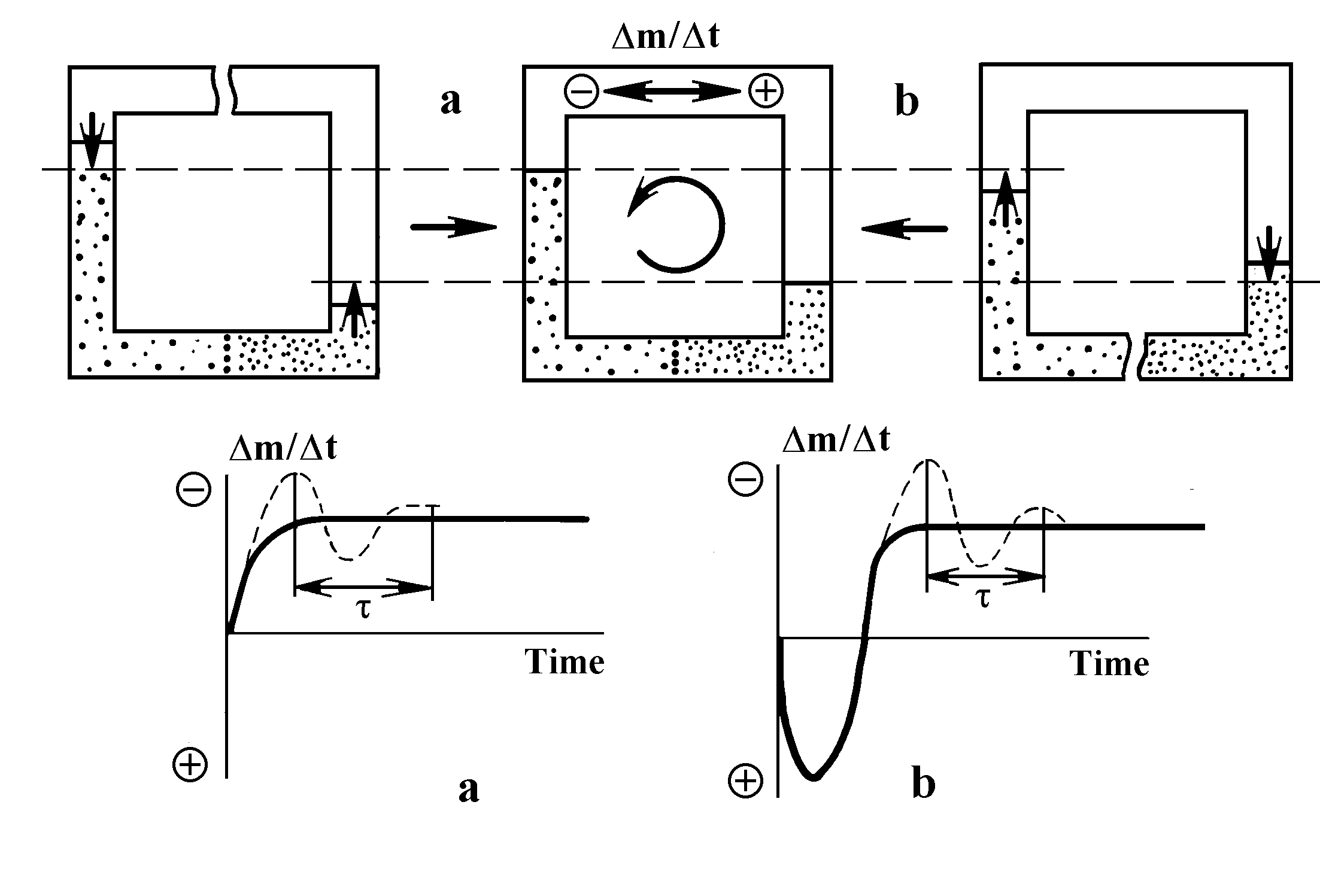
Fig.8. Two different kinetics for transition of the osmotic koltsar into the circulational mode from two different stationary states (dashed line depicts decaying oscillations with characteristic period t that accompany mass transfer velocity enter to the plateau).
4. Electrophysical koltsar
4.1. Problem formulation
Since there exists a certain formal analogy between liquid moving in pipes and current in wires, there is reason to consider an electrophysical analogue of the osmotic koltsar where the conductivity electrons play the role of solvent molecules, and the semiconductor, of the semipenetrable partition. In such a system will charge carriers circulate like liquid molecules in the Lazarev or osmotic koltsars?
The answer will be Yes if, besides the current generation effect, one detects in the device schematized in Fig.9 two different stationary states, that is, two different kinetics of current entering the plateau.
If two metals with different electron work functions are brought in contact, the so-called contact potential difference appears between them
![]() , (7)
, (7)
where E1 and E2 are the electron work functions of Metals 1 and 2, respectively, and e is the electron charge. No useful work, yet, can be produced by this potential difference, because if the ends of a dipole are closed by a third conductor, between it and Metals 1 and 2 contact potential differences will also occur such that the electron gets no additional energy by making a complete turn around the closed loop. Yet, it is often overlooked that motion of bodies (conductivity electron including) is controlled not by energy, but by forces that can create two stationary states and, thus, generate circulation that does not violate the energy conservation law.

Fig.9. Diagram of electrophysical koltsar: a, b — metals with different electron work functions and concentrations of conductivity electrons, c — semiconductor.
The point is that apart from the contact potential difference D j ![]() another potential difference, D j
another potential difference, D j ![]() appears due to the difference in concentrations of charge carriers n01 and n02 in Metals 1 and 2
appears due to the difference in concentrations of charge carriers n01 and n02 in Metals 1 and 2
![]() .
.
In their turn, the concentration of conductivity electrons in metal can be regarded in the classical approximation as equal to
![]() ,
,
where NA is the Avogadro number, and k , A and r are, respectively, valence, atomic weight and density of the metal. Whence,
![]() . (8)
. (8)
As follows from (7) and (8), D j ![]() and D j
and D j ![]() are absolutely independent of each other, because one (D j
are absolutely independent of each other, because one (D j ![]() ) is defined by interaction of electrons with the crystal lattice of metal (i.e., the work function is counted from the Fermi level), and another (D j
) is defined by interaction of electrons with the crystal lattice of metal (i.e., the work function is counted from the Fermi level), and another (D j ![]() ) depends on the characteristics of crystal lattice atoms such as valence, mass and ability to interact with each other. That is why D j
) depends on the characteristics of crystal lattice atoms such as valence, mass and ability to interact with each other. That is why D j ![]() and D j
and D j ![]() of various contact pairs can have either identical, or opposite signs. For example, if the values of D j
of various contact pairs can have either identical, or opposite signs. For example, if the values of D j ![]() and D j
and D j ![]() of the Indium-Nickel pair as computed through (7) and (8) are +400 and -11.7mV, respectively, for the Beryllium-Silver pair they are, respectively, +400 and +35.7mV. This fact defines ability of a system consisting of two contacting metals to be in two different stationary states that are defined, one by the electron work function, and another by charge carrier concentration.
of the Indium-Nickel pair as computed through (7) and (8) are +400 and -11.7mV, respectively, for the Beryllium-Silver pair they are, respectively, +400 and +35.7mV. This fact defines ability of a system consisting of two contacting metals to be in two different stationary states that are defined, one by the electron work function, and another by charge carrier concentration.
Comparison of the osmotic koltsar and its electrophysical analogue, suggests that the roles of hydrostatic pressure and saturated vapor are played in the bimetallic system by electron interaction with crystal lattice (defining the work function) and charge carrier concentration, respectively. When Metals 1 and 2 that are initially under identical potentials conventionally regarded as zero, are connected by a conductor, a current appears in it whose direction depends on the ratio of work functions. When the potential difference between the metals becomes D j ![]() , the work functions should become equal and the primary current vanishes. In the general case, however, the charge carrier concentrations in Metals 1 and 2 will not be equal under potential difference D j
, the work functions should become equal and the primary current vanishes. In the general case, however, the charge carrier concentrations in Metals 1 and 2 will not be equal under potential difference D j ![]() , and there will be a secondary current in the conductor defined by the sign and value of D j
, and there will be a secondary current in the conductor defined by the sign and value of D j ![]() . In its turn, this will violate the initial equality of work functions and again cause current in the conductor, etc. Stated differently, two different metals connected by a conductor are in dynamic equilibrium defined by the potential difference D j 12 = D j
. In its turn, this will violate the initial equality of work functions and again cause current in the conductor, etc. Stated differently, two different metals connected by a conductor are in dynamic equilibrium defined by the potential difference D j 12 = D j ![]() +D j
+D j ![]() .
.
In the setup of Fig.9, there should be the same charge redistribution processes. However, because of its asymmetry introduced by the semiconductor, the secondary charge carrier redistributes as defined by D j ![]() can take place in a closed loop. This implies that in the electrophysical koltsar there should be current whose value and direction are defined by the sign and values of D j
can take place in a closed loop. This implies that in the electrophysical koltsar there should be current whose value and direction are defined by the sign and values of D j ![]() and semiconductor resistance. Since D j
and semiconductor resistance. Since D j ![]() is of the order of tens of mV, current of the order of 10-9-10-10 A must exist in the circuit with resistance of the order of tens of MOhms. Experimental measurement of such a current is a feasible task.
is of the order of tens of mV, current of the order of 10-9-10-10 A must exist in the circuit with resistance of the order of tens of MOhms. Experimental measurement of such a current is a feasible task.
4.2. Materials, instrumentation and methods7
The specimens for study were prepared by thermal deposition in high vacuum of thin layers (10 - 20 mcm) of Aluminium and Silver or Silver and Beryllium (purity at least 99.99%) on the opposite sides of wafers (diameter 30 - 40mm, thickness 0.2-0.8mm) cut of monocrystals of Gallium phosphide (p- and n-types), Indium phosphide (n-type) and Gallium phosphide-based p/n junctions. Specimen numbers, their structure and the results of qualitative tests for the ability to generate current are tabulated below.
|
Specimen N |
Specimen structure |
Wafer thickness |
Effect availability |
|
1 |
Ag-p[GaP]p-Al |
0.8 mm |
- |
|
2 |
Ag-n[GaP]p-Al |
0.8 mm |
+ |
|
3 |
Ag-p[GaP]n-Al |
0.8 mm |
- |
|
4 |
Ag-n[GaP]n-Al |
0.8 mm |
+ |
|
5 |
Ag-n[InP]n-Al |
0.8 mm |
- |
|
6 |
n[GaP]n (control) |
0.8 mm |
- |
|
7 |
Ag-n[GaP]n-Al |
0.2 mm |
+ |
|
8 |
Ag-n[GaP]n-Be |
0.2 mm |
+ |
The preliminary qualitative tests of the specimens were carried out by means of a simplistic mirror microamperemeter. With scale factor 1mA, closure of the circuit with Specimens 2 and 4 provided light spot deviation by 3 -5 divisions, changes in polarity of the specimens used resulted in changes of current direction. Specimens 1, 3, 5 and 6 (control) generated no current.
For all subsequent quantitative measurements, the electrometric high-resistance voltmeter V7 -45 (V.I. Lenin factory, Minsk, Belorussia) was used to measure currents within the range from 10-7 to 10-17A. According to the certificate, the zero drift is not more than 10-17A over 24 hours of continuous work; the rms noise amplitude at the analogue output is 2Ч 10-18A at most. Measurements were carried out in the subranges 10-9 -10-10A in three different modes:
- numerical indication and instrument memory;
- recorder connected to the analogue output;
- computer interfaced to the analogue output via ADC.
The specimens under study were placed either directly in the closed measurement chamber of the instrument and connected to the circuit by two copper electrodes (diameter 50mm, thickness 5mm) with silvered contact surfaces (Fig.10), or in an external screened grounded Permalloy chamber (Fig.11). The specimen voltage-current characteristics were measured by the cheme shown in Fig.12.
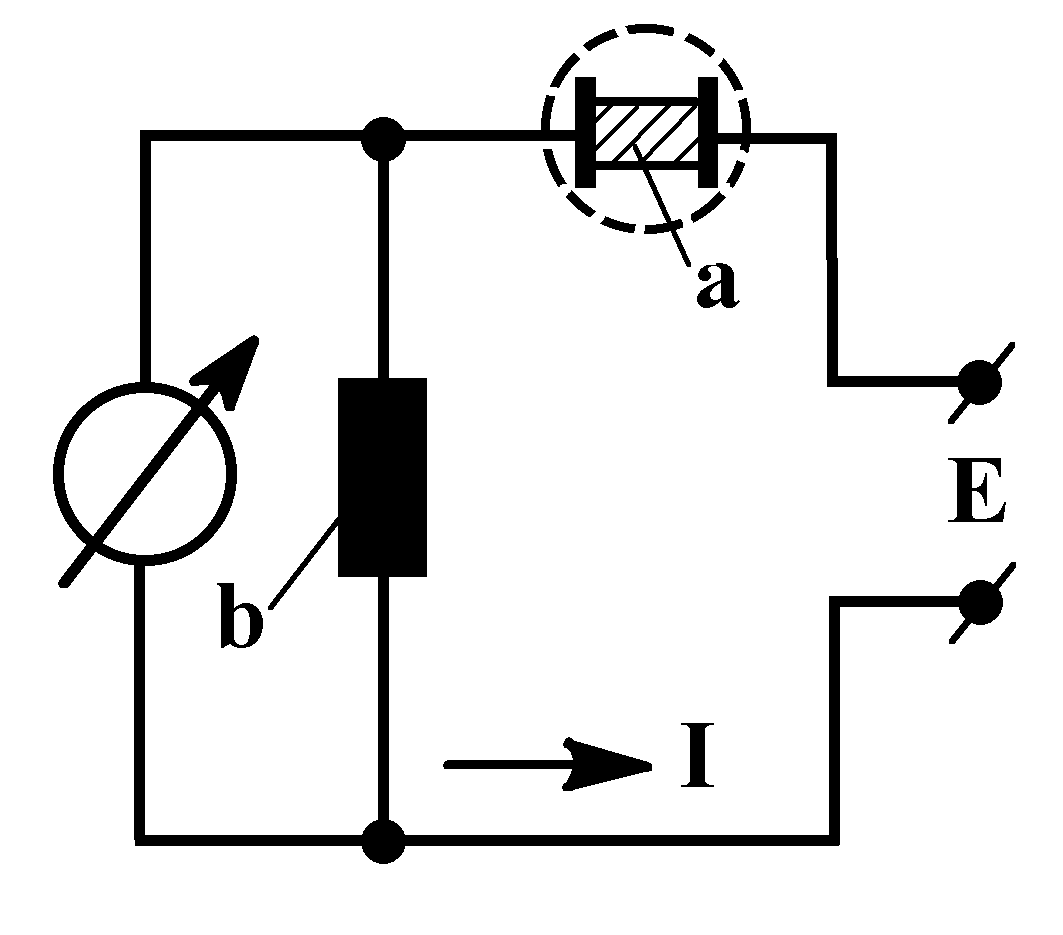
Fig.12. Diagram of voltage-current characteristic (VCC) measurement: a — specimen, b — load resistance (9.1MOhm).
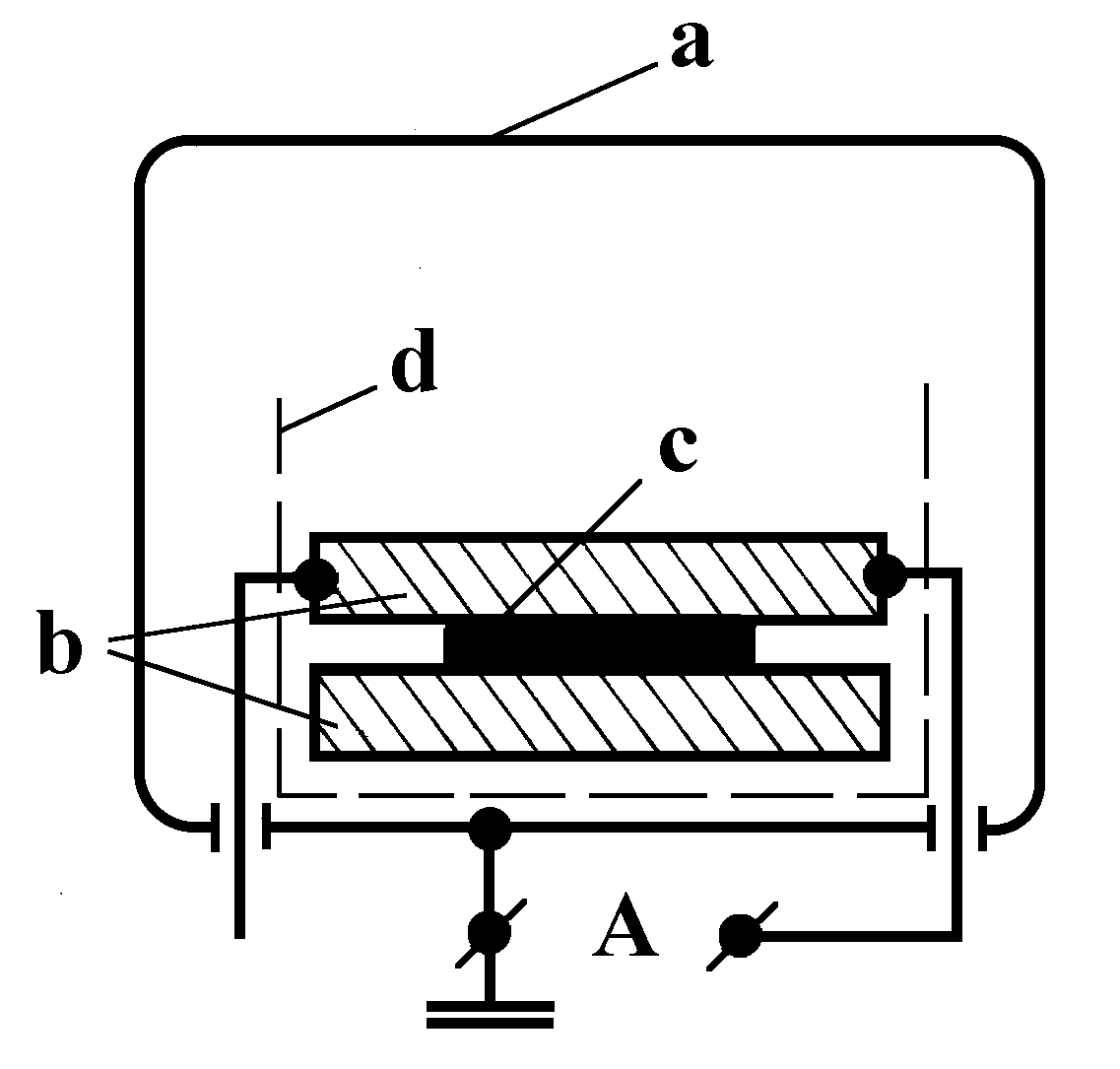
Fig.10. Position of specimens in the measuring chamber: a — chamber, b — copper electrodes with silvered contact surfaces, c — specimen, d — polyethylene isolation.
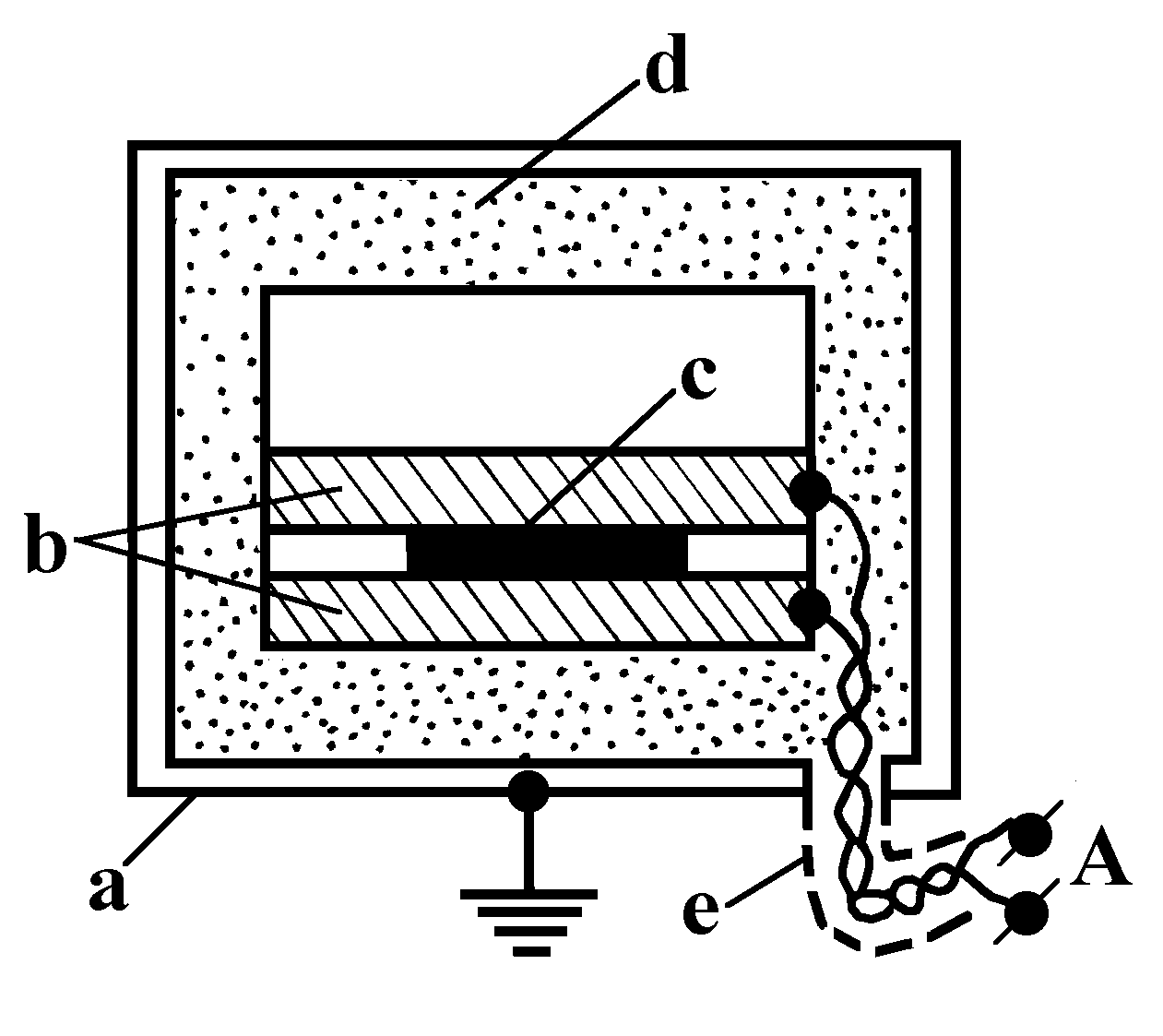
Fig.11. Position of specimens in external measurment chamber: a — grounded Permalloy screen, b — copper electrodes, c — specimen, d — Teflon isolation, e — screened grounded cable.
4.3. Experimental results and discussion
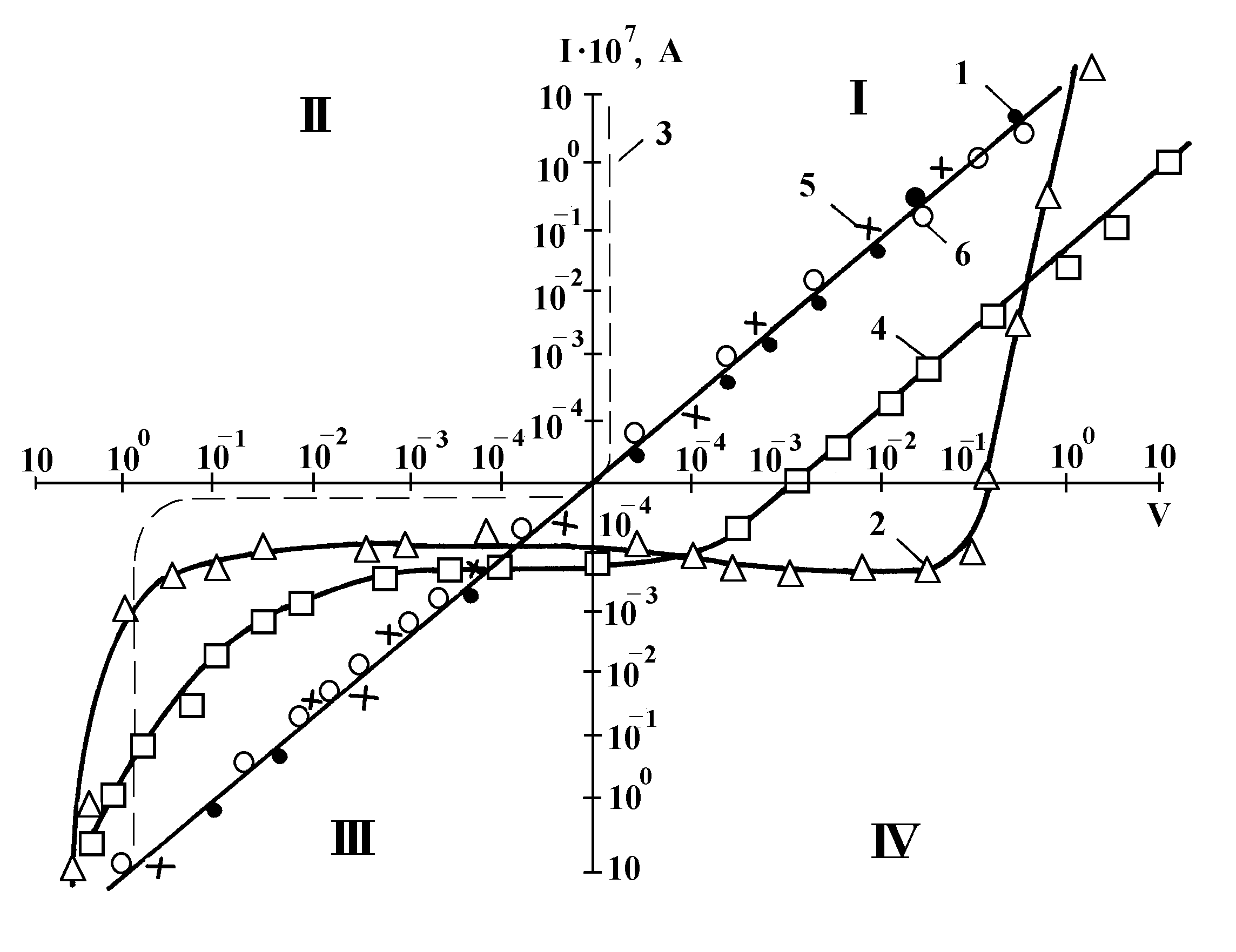
The measurements of voltage-current characteristics confirmed the above described qualitative tests and revealed somewhat unusual electrophysical properties of the specimens (Fig.13). If, for example, Specimens 1, 5 and 6 (that is, the bimetallic systems based on p-type Gallium phosphide and n-type Indium phosphide, and the control specimen of Gallium phosphide without the bimetallic cover) that do not generate current have standard linear voltage-current characteristics, those of 2, 3 and 4 feature pronounced nonlinearity. The nonlinearity of Specimen 3 differs essentially from that of 2 and 4. Like Specimens 1, 5 and 6, Specimen 3 generates no current, but its voltage-current characteristic has the form peculiar to the usual diodes when a cutoff potential is applied to them, in that it goes through the origin and is sharply asymmetrical. Contrastingly, the voltage-current characteristics of Specimens 2 and 4, are symmetrical, but go through the negative-resistance area (quadrant IV), that is, these specimens are active current sources. Specimen 4 features another interesting anomaly requiring further investigation — it demonstrates “memory” of a kind (Fig.14).
Fig.13. Voltage-current characteristics of different specimens (each point is the average of 600 readings made in 60 sec): Specimens 1, 5 and 6 do not generate current and feature usual linear VCCs; at application of cutoff potential Specimen 3 has diode-like VCC and generates no current; Specimens 2 and 4 generate current and feature symmetrical VCCs passing through the negative-resistance area (quadrant IV).
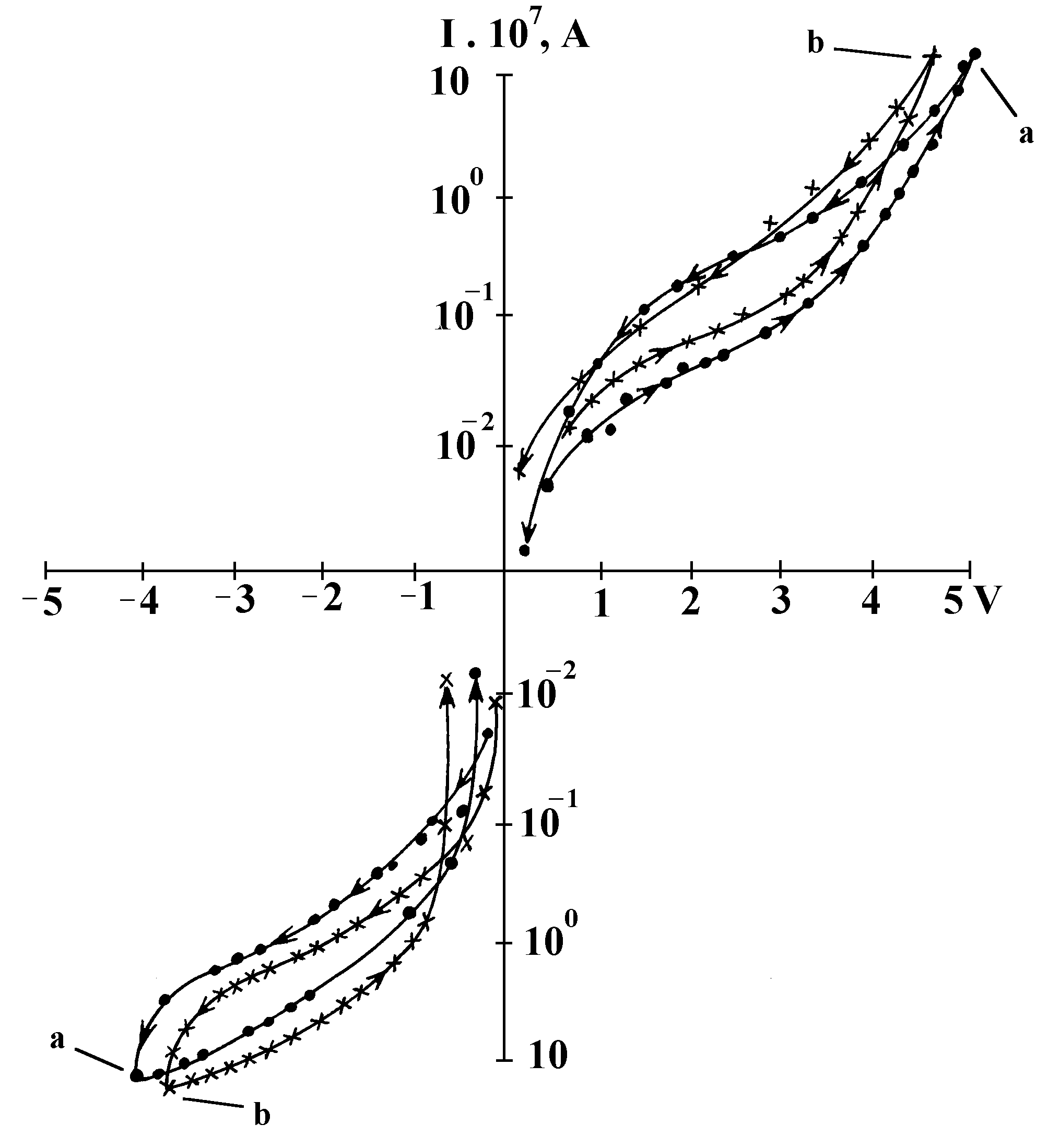
Specimens 2 and 3 differ only in orientation with respect to the same p/n junction of oppositely charged metals. The essential difference in their voltage-current characteristics can be explained by the fact that in Specimen 3 charge orientation assists in increasing resistance of the double electrical layer on the p/n junction, and in Specimen 2, in decreasing resistance. The calculated value of D j ![]() for the Silver-Aluminium pair is about -28mV. The recorded direction of current generated by Specimen 4 demonstrates precisely that Silver has negative charge, and Aluminium, positive. Specimen 4 lacks p/n junction. Nevertheless, its voltage-current characteristic is similar to that of 2, and not of 3 or 1, 5 and 6. Specimens 2 and 4 generate current of the order of 10-9-10-11A and develop emf of the order of tens mV, that is, close in value to D j
for the Silver-Aluminium pair is about -28mV. The recorded direction of current generated by Specimen 4 demonstrates precisely that Silver has negative charge, and Aluminium, positive. Specimen 4 lacks p/n junction. Nevertheless, its voltage-current characteristic is similar to that of 2, and not of 3 or 1, 5 and 6. Specimens 2 and 4 generate current of the order of 10-9-10-11A and develop emf of the order of tens mV, that is, close in value to D j ![]() .
.
Fig.14. Hysteresis phenomena observed in Specimen 4: a — each point is the average of 100 readings made in 10 sec, b — each point is the average of 300 readings made in 30 sec.
Generally speaking, such emf might also be due to some trivial factors, but they can show to have no bearing on the effect of current generation as observed in the koltsar.

Fig.15. Current generated by Specimen 4 vs. measurement chamber temperature.
Temperature difference of the electrodes contacting different sides of specimens. It is true that the generated current varies with specimen temperature (Fig.15). This effect, however, is evidently due to the decrease of semiconductor resistance under practically constant koltsar emf, because a thermoelectromotive force of the order of 1mV can occur at temperature difference of the order of 30° C, but such a gradient never occurred experimentally — the gap between the massive copper electrodes being less than one millimeter, the temperature gradient could hardly be more than tenth fractions of a degree. This factor can be rejected as a possible source of current generation also because rotation of the specimen by 180° (at the same polarity of electrodes) results in current of opposite direction, which would not be the case had the temperature gradient been the cause of current.
Physicochemical and chemical ageing processes. Processes such as diffusion of metal atoms into semiconductor and/or their chemical interaction could, in principle, create emf, all the more so that the electrophysical koltsar develops a very moderate power of the order of only 10-11-10-14 W. Then, Specimens 1 and 5 should be able to generate current, which is not the case. The conclusive proof that the observed phenomenon is indeed the koltsar effect is offered by pronounced kinetic indications that two different stationary states exist in Specimen 4, which is the principal distinction of the koltsar from other usual current sources. Namely, if the metals on the surface of high-resistance semiconductor are grounded, their potentials are identical, and the electron work functions, different (State 1). If the metals are short-circuited by a third conductor, potential difference occurs between them and the electron work functions tend to become equal (State 2). As shown in Fig.8, connection to the measurement circuit of so prepared specimens (that is, after preliminary grounding or short-circuiting) should be accompanied by two different kinetics of entering the plateau. The usual current source cannot give such an effect in the measurement circuit. Connection of Specimen 4 to the measurement circuit enabled one to observe precisely two different kinetics corresponding to two stationary states (Fig.16), which attests unambiguously to the fact that the system is a real electrophysical koltsar. (It might be well to note in parentheses that current generated by koltsar should be called Galvani current, whereas that generated by the galvanic cells, Volta current.) Correctness of the analogy between the osmotic and electrophysical koltsars is corroborated by that current entering the plateau is accompanied by decaying harmonic oscillations featuring amplitudes, periods and decay times inherent to each particular specimen (Fig.17). Exactly the same oscillations occurred when pulse current was excited in the measurement circuit (Fig.18), which is indicative of the fact that oscillation period and decay time are defined by the RC characteristics of the specimens.

Fig.16. Two different kinetics of entering the plateau indicating to two different states in Specimen 4: a — prior to switching the measurement circuit ON, the specimen electrodes are grounded, b — prior to switching the measurement circuit ON, the specimen electrodes are shot-circuited (t ~ 40 sec).
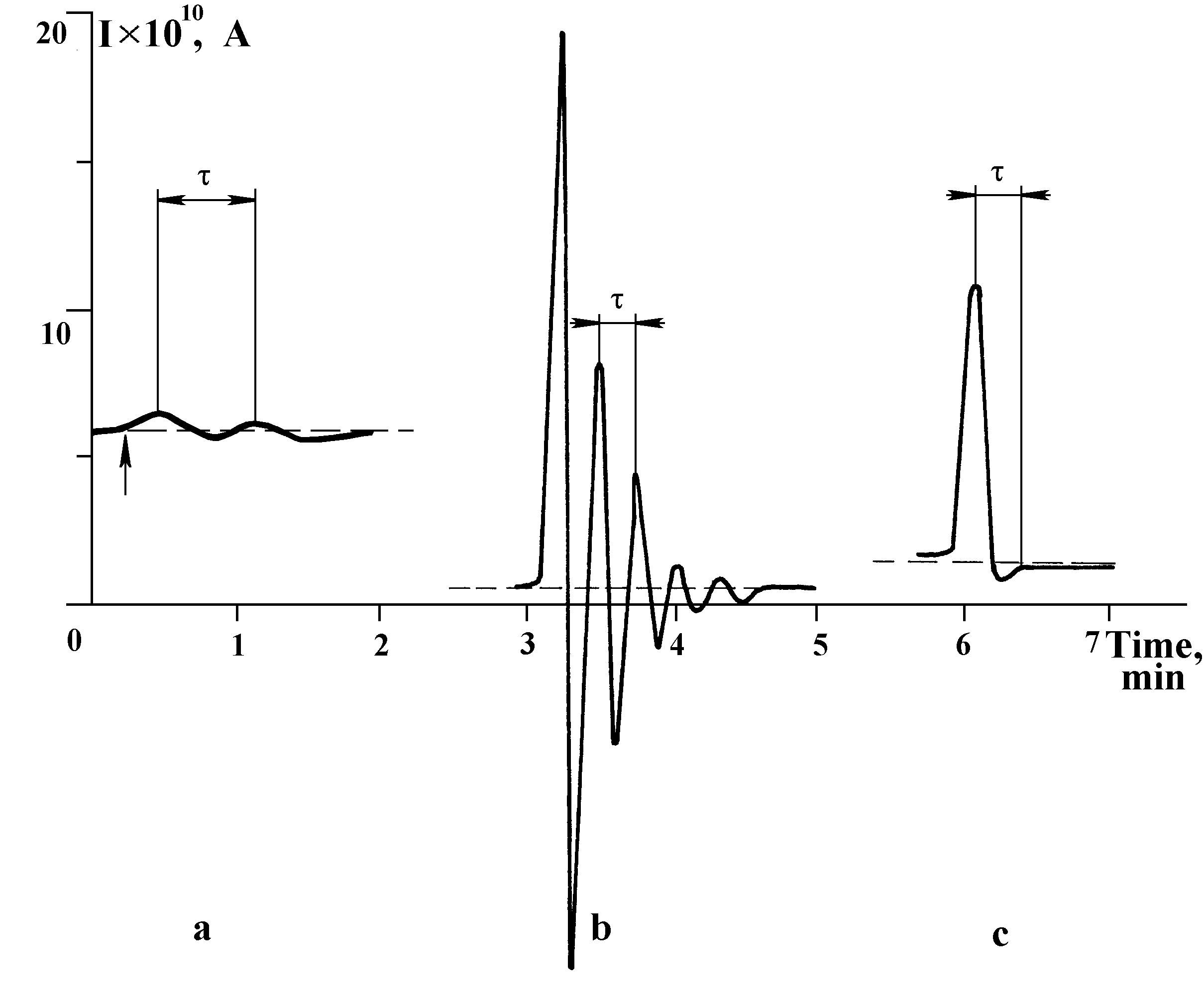
Effect of natural and/or artificial external electromagnetic inductions. The decaying harmonic oscillations shown in Fig.18 appeared in the measurement circuit because of a pulse magnetic field created by a permanent magnet of intensity of about 100 Oersted that was carried quickly past the measurement chamber, the specimen being inside it or outside, in an external measurement chamber. The specimens themselves proved to be completely insensitive to the magnetic field of such intensity. Fundamentally, the geomagnetic field varying with amplitude 10-2 Oersted at most can excite in the measurement circuit harmonic current oscillations with amplitude not exceeding 10-12A (Specimen 7) and 10-14A (Specimen 4), but it cannot excite direct current, because, judging from its voltage-current characteristic, Specimen 4 does not feature diode characteristics. Besides, the measurement circuit is least sensitive to excitation by pulse magnetic field precisely for Specimen 4 generating a maximal current. As for the high radio-frequency radiation, it is sufficiently well screened by the measurement chamber walls, to which stable operation of the instrument in subranges down to 10-15A attests. The walls play the role of the Faraday cage screening the measurement circuit and the specimens also from the electrostatic fields.
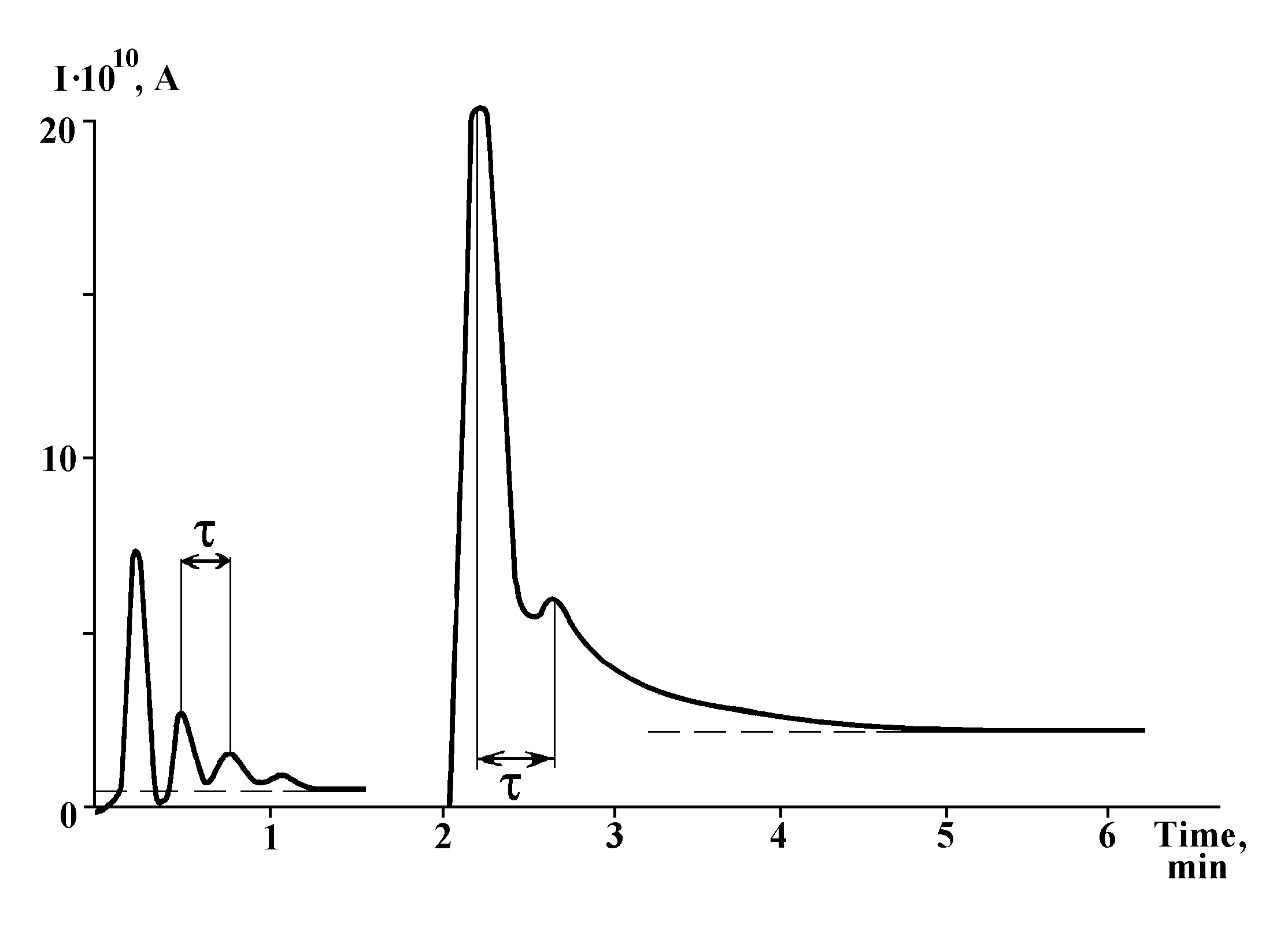
Fig.17. Current plateau entering kinetics as observed with different specimens: a — Specimen 7 (t ~ 15 sec), b — Specimen 8 (t ~ 25 sec).
Since there exist no other trivial factors causing current in the elecrophysical koltsar, the observed effect (of spontaneous current circulation in nonsuperconductive ring at room temperature8) can be regarded as a fundamentally new and previously not observed natural phenomenon. The koltsars are thermodynamically reversible nonlocal classical objects (they may also be called dynamic dissipative structures) whose plausibility was first suggested by Kozyrev.
The electrophysical koltsar has another property following from its nonlocality — observed in it (at least, partially) are fluctuations of explicitly cosmophysical origin. Their study is the subject of concluding part of the present experimental research.
The currents generated by the specimens under consideration differ not only in value (that was noted to vary from experiment to experiment, sometimes appreciably and without any evident cause), but also in the nature of fluctuations that were recorded continuously.
Specimen 4, for example, generates the greatest current with smallest fluctuation amplitude; the small current of Specimen 7 has greater fluctuation amplitude making it to change even its direction, the current fluctuations of Specimen 8 are also significant, but do not result in changes of the effect sign (Fig.19). The choice of Specimen 4 for further methodical study of current fluctuations dwells on a simple reason that they cannot be classified as simple instrumental noise, but are related explicitly to the current itself.
Fig.18. Occurrence of decaying harmonic oscillations after excitation of pulse current in the measurement circuit: a — Specimen 4 (t ~ 40 sec); b — Specimen 7 (t ~ 15 sec); Specimen 8 (t ~ 25 sec).
First, it might be well to note that current fluctuations as generated by the electrophysical koltsar have the nature of nonequilibrium noise of 1/f type with pronounced harmonics. If the constant current component that can be regarded as fluctuation of frequency f® Ґ is compensated, an extended, yet a clearly pronounced maximum is observed in the power spectrum in the domain 0.4 - 0.8 cps (Fig.20). Although the general form of the spectrum in time remains invariable, in details it varies continuously, as if “breaths”, which, by the way, provides another proof in favor of koltsar current being due to anything but temperature. Since only usual small-amplitude noise is observed in the domain of higher frequencies limited by the cycle frequency of voltmeter V7 -45 (10 cps), attention was focused on the low-frequency spectrum domain.

Fig.20. Fluctuations of current generated by Specimen 4: above — the signal; below — signal power spectrum after compensation of the constant current component.
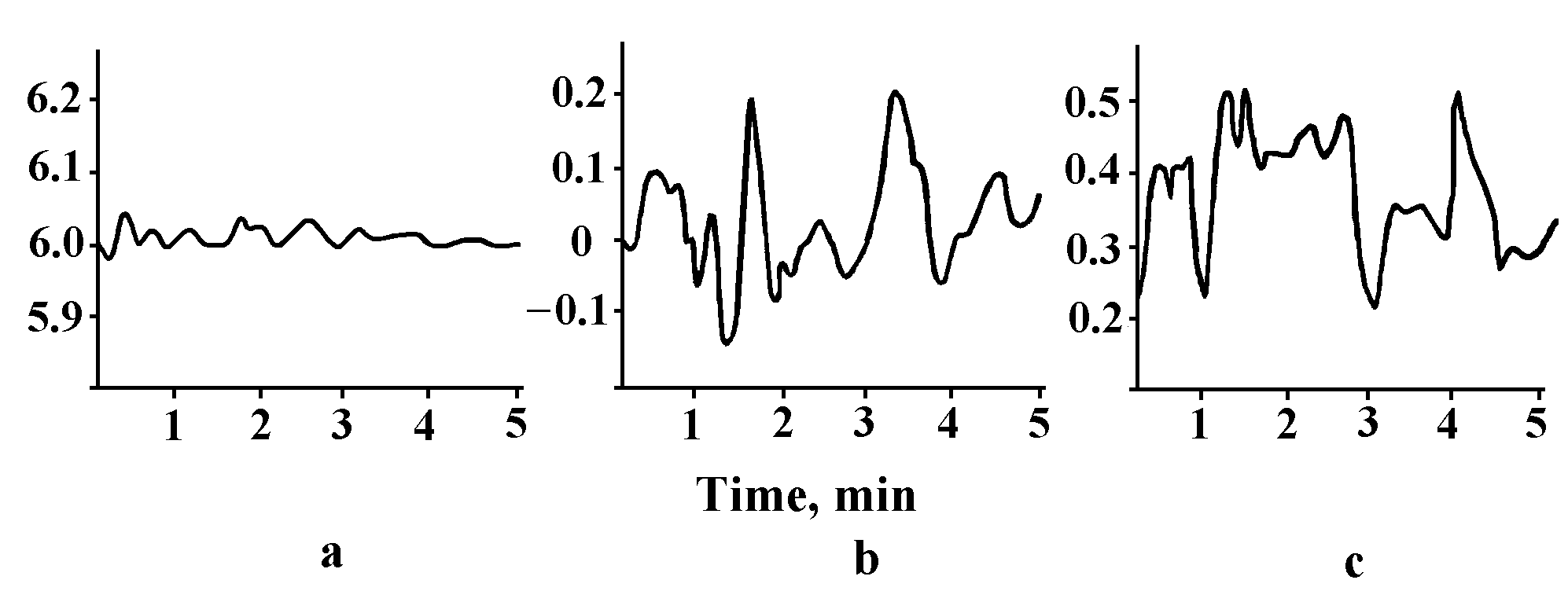
Fig.19. Fluctuations of current generated by different specimens (with integration constant of 10 sec): a — Specimen 4, b — Specimen 7, c — Specimen 8.

To this end, a long measurement run was carried out of the current generated by Specimen 4 (72 days of continuous observation), readings being made each 15min with integration constant 100sec. Figure21 depicts a typical current profile for the same time of the day. It is not only significant fluctuation amplitude (for current of about 1.5Ч 10-10A, the instrumental error was about 3Ч 10-12A at most) that engages attention, but also the fact that daily average current can either be constant, or change sharply under practically constant temperature (± 0.2° C), that is, where the temperature drift (see Fig.15) could not be over about 2Ч 10-12A. Examination of long-term observations convinces that current fluctuations are of explicitly cyclic, and not random, in nature (Fig.22).
Fig.21. Fluctuations of current generated by Specimen 4 at the same period of time of different days (LT, local time, Moscow): a — June 1, 1992; b — June 2, 1992; c — June 3, 1992.
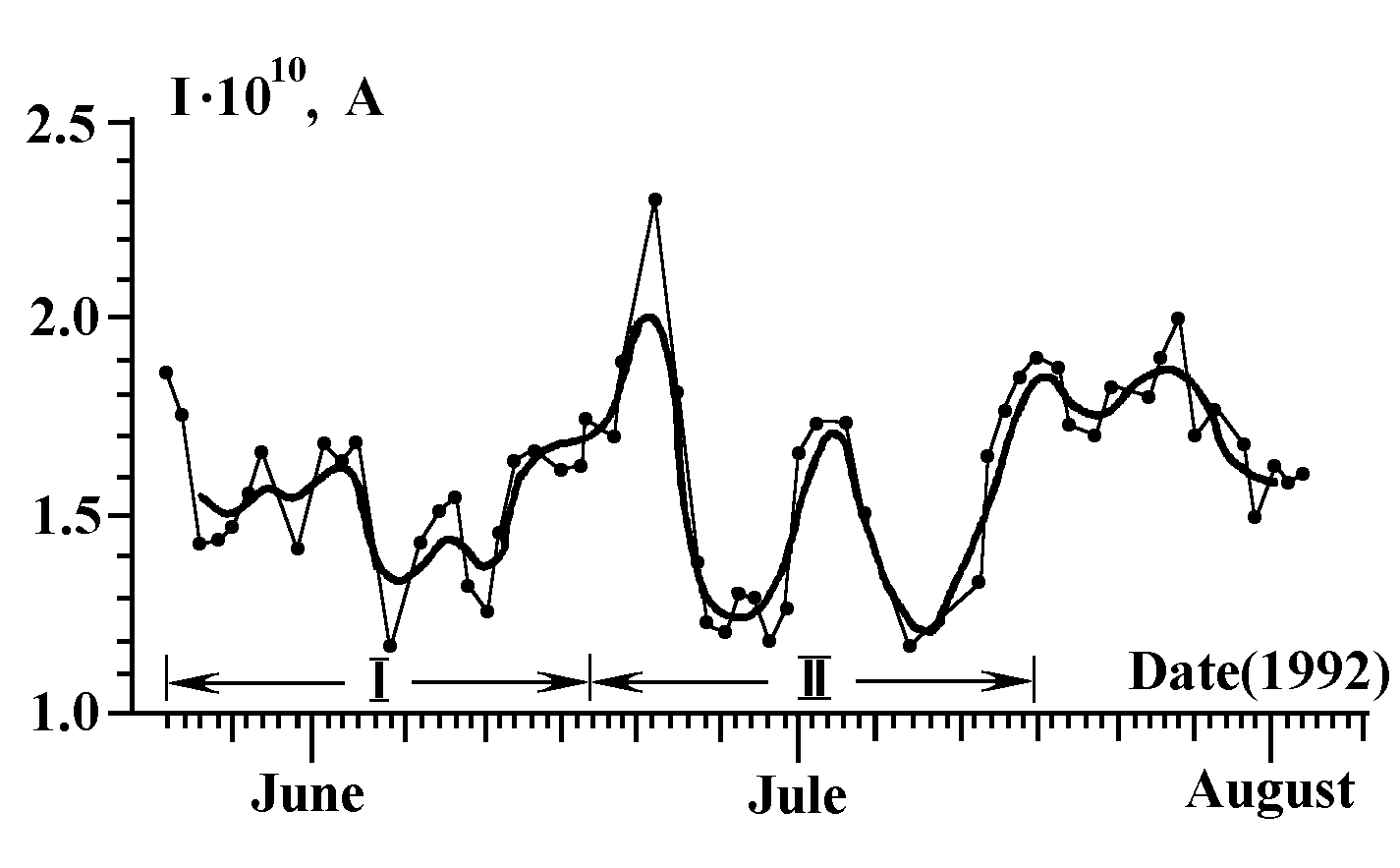
On the average, the current generated by the electrophysical koltsar is constant over a long time, but continuous fluctuations, sometimes with significant amplitude, go on against this background. By and large no significant relation was observed between these fluctuations and variations of measurement chamber temperature, individual sharp peaks (June 21, for instance) most likely being attributable to the temperature factor (Fig.23). Yet the rhythm of current fluctuations (confidence period about 33 days) coincides amazingly with that of Sun activity (period about 32 days) observed at the same season (Fig.24) and has some features in common with the rhythm of variations in the general planetary geomagnetic perturbation.
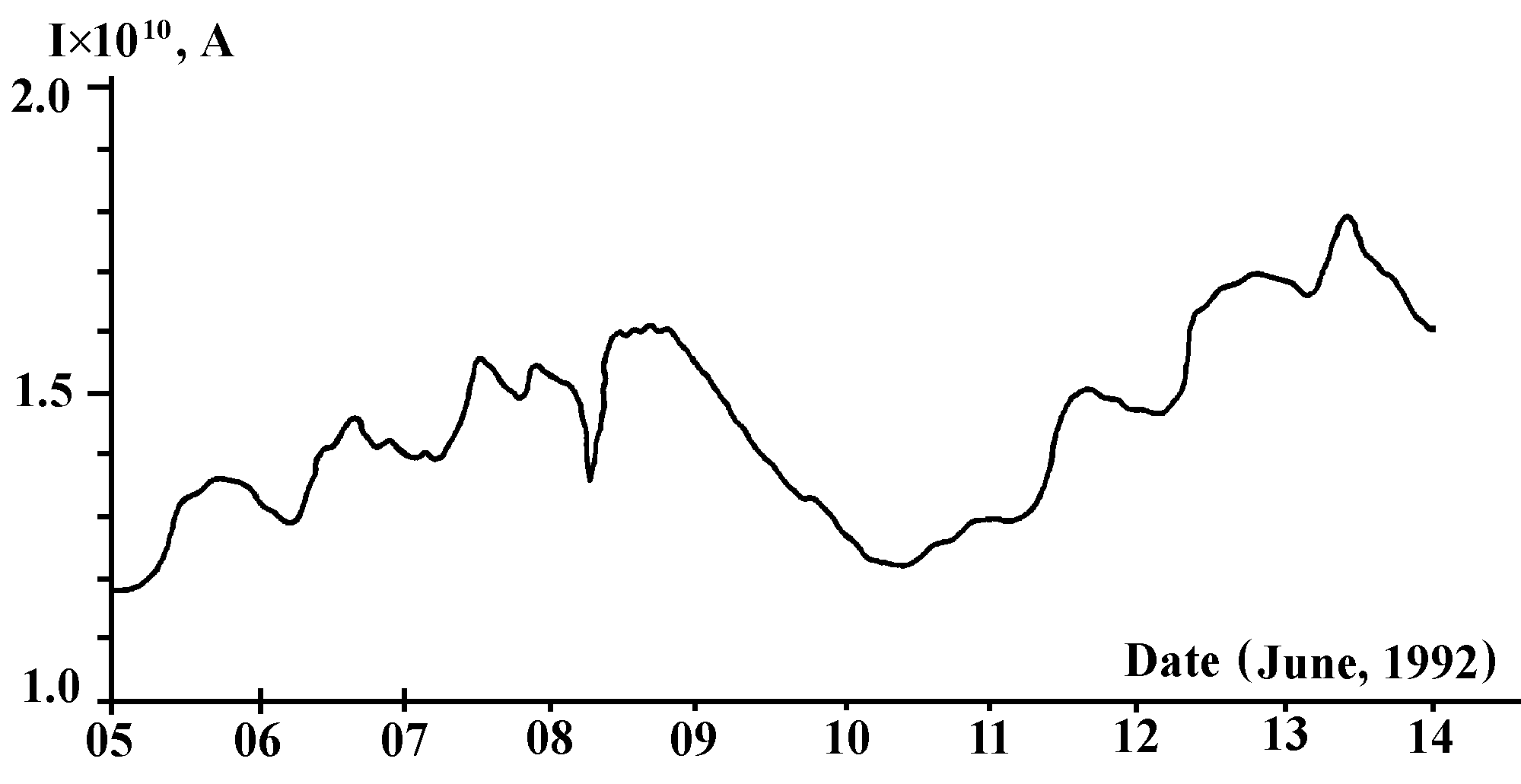
Fig.22. Fluctuations of current generated by Specimen 4 as recorded continuously over 9 days. One can see a well pronounced cycle of about 6 days (the mean time of passing the interplanetary magnetic field by the Earth is about 7 days).
The mutual correlation functions of current fluctuations, Sun activity changes and geomagnetic perturbations provide a better insight into the causes of general rhythms (Fig.25) enabling the following conclusions:
1. Current fluctuations in the electrophysical koltsar are related explicitly to Sun activity changes and are carried from the Sun to the Earth by solar wind (the observed delay of about 5 days is characteristic of the solar-terrestrial relationships, including solar-biospheric ones).
2. Variations of geomagnetic field perturbation have no direct effect on current fluctuations in the electrophysical koltsar, but are related to it indirectly through various components of solar wind — most probably they are due to a special cosmophysical factor exerting specific influence on the biosphere (Zhvirblis 1989).
3. There is a slight indication to correlation without phase shift between current fluctuations in the electrophysical koltsar and solar activity variations (inflection of the function rc at 0d noted also in the Lazarev’s experiments), that is, to the plausibility of fast (instantaneous?) solar-terrestrial relations, or (more likely) to synchronism of solar activity and koltsar power fluctuations, because both objects are subjected to the action of the same nonlocal cosmophysical factor.
Fig.23. Fluctuations of daily average current generated by Specimen 4 (each point is the average of 90 readings with 15-min interval); the sections denoted as I and II were used for processing by the superimposed epoch method (see Fig.27 below).
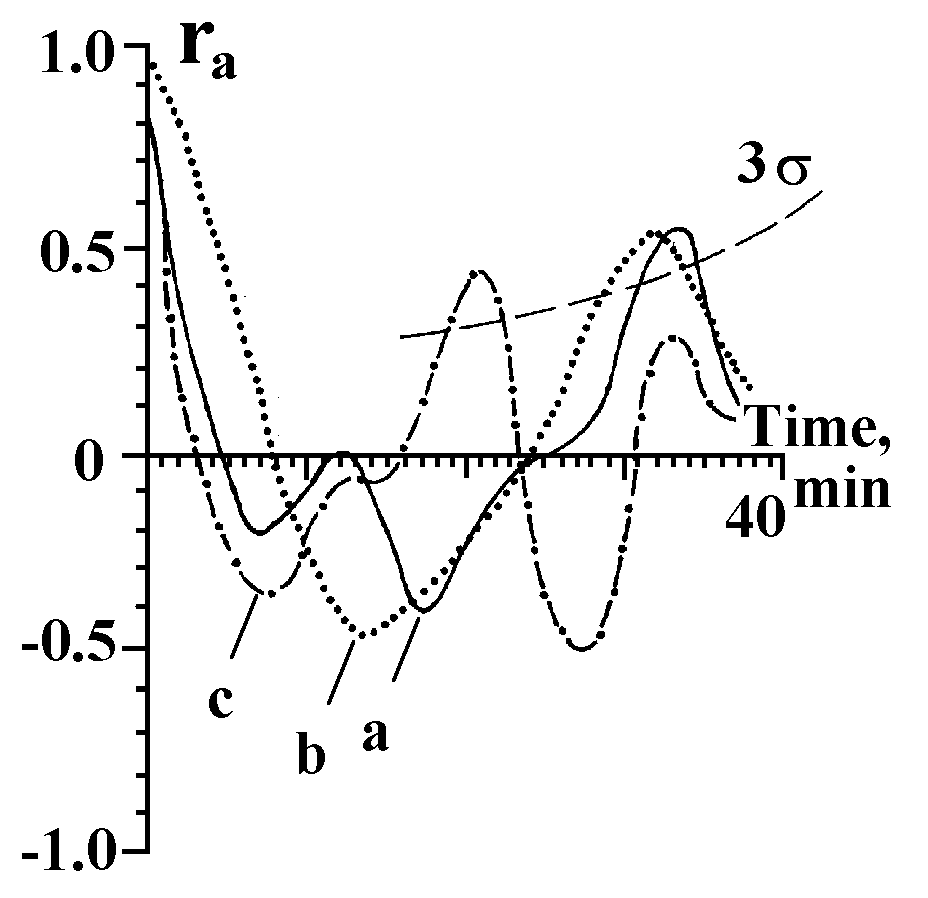
Fig.24. Autocorrelation functions (ra): a — fluctuations of current generated by Specimen 4; b — Sun activity variations (international indices Ri are used); c — variations of daily average general geomagnetic field perturbation (Ap-indices). The confidence level 3s (p<0.005) exceeded by the periods ~33d, ~32d and ~21d.

Fig.25. Corss-correlation functions (rc): a — Specimen 4 current fluctuations and Ri-indices (solar activity); b — current fluctuationas and Ap-indices (geomagnetic activity); c — Ap- and Ri-indices. The dependences of current fluctuations and genomagnetic perturbations on solar activity are identical, but there is no direct relation between current fluctuations and deomagnetic perturbations.
Two more observations stress the uncommonness of the cosmophysical factor responsible for the koltsar effect and for realization of the solar-biospheric relationships. First, attempts to eliminate current fluctuations in the electrophysical koltsar by screening low-frequency electromagnetic fields give no appreciable effect (Fig.26); besides, no variations in the constant current component are observed. Second, when well reproducible regular daily components were extracted from current fluctuations by the superimposed epoch method (Fig.27), they turned out to bear a striking resemblance to the regular daily components of azimuth variations of the major axis of polarization ellipsis of the so-called micropulsations of the geomagnetic field Pc3 (i.e., its orientation with respect to the terrestrial meridian), the two absolutely different processes being amazingly synchronous.
The micropulsations Pc3 lie within the frequency range 0.02 - 0.1cps, the magnetic vector oscillation amplitude is about 5Ч 10-6Oersted, and the vertical electrical component — a few V/m. This cosmophysical factor was found to be closely related to solar activity manifestations, and is assumed to play an important role in the solar-biospheric relationships. This factor is still too weak to cause conspicuous physical effects, all the more so that it should be attenuated strongly by the grounded Permalloy screen. In general, the position of the major axis of electromagnetic oscillation polarization ellipsis has no relation to their energy characteristics and exerts no influence on their interaction with the substance. Therefore, if the noticed synchronization between the fluctuations of electrophysical koltsar-generated current and the variations of the polarization ellipsis major axis azimuth of micropulsations Pc3 is not occasional, it can be due only to changes in the physical properties of the space where the substance occurs and where the electromagnetic waves pass.
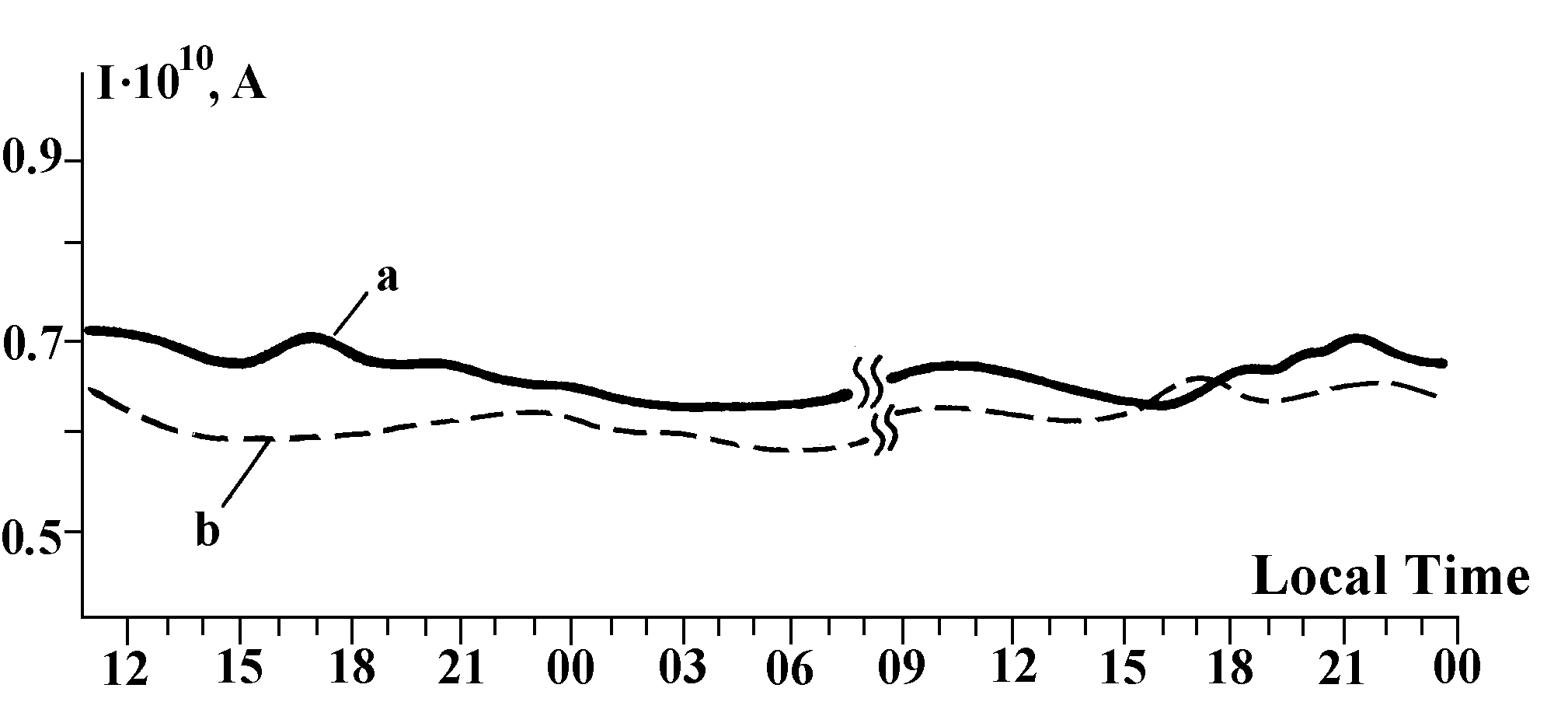
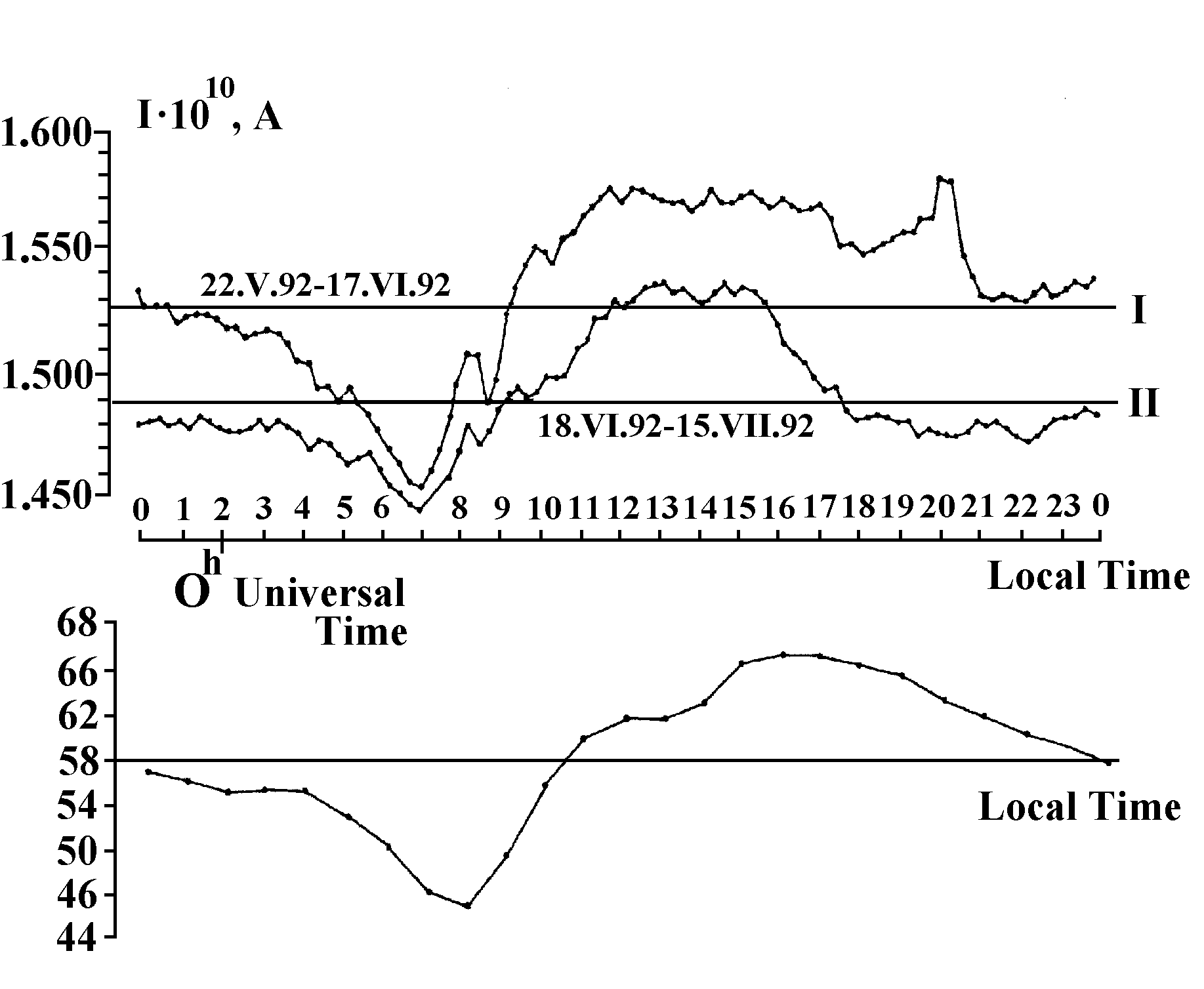
Fig.26. The results of checking the effect of possible external electromagnetic inductions in the electrophysical koltsar: a — the specimen in a nonscreened external measurement chamber (no protection against external influences); b — the specimen in an external measurement chamber with grounded Permalloy screen (see Fig.11).
It seems that the direct cause of koltsar-generated current fluctuations are the changes in electron work functions, that is, minor fluctuations in height of potential barriers (this, in particular, can account for the macrofluctuations in precise physical measurements). In their turn, potential barrier height variations in the electrophysical koltsar must result in the corresponding redistribution of charge carriers between the double electrical layers and, as a result, to occurrence of fluctuations of the main current in measurement circuit (Zhvirblis 1992). Therefore, the electrophysical koltsar might prove to be extremely promising for methodical study of macrofluctuations observed in systems of different nature (it is but logical to assume that they are due to changes in potential barrier height), because here the output is the direct consequence of its own cause, and requires only corresponding amplification and handling.
Fig.27. Regular daily current fluctuation components of Specimen 4 (extracted by the superimposed epoch method, see Fig.23), and variations of azymuth q of the major axis of polarization ellipsis of micropulsations of geophysical field Pc3 (data of the Borok Laboratory, Russia).
5. Koltsar thermodynamics
5.1. Conservatism and variability
The existence of physical interaction forces giving rise to two different stationary states is the direct cause of koltsar effect, circulation of liquid or of charge carriers. The existence of physical interaction forces (and, thus, potential barriers of one or another height) accounts for our existence in the world of finite-dimensional stationary objects that are capable, in principle, to change. Stated differently, conservatism and variability, which are generally recognized as foundations of life and biological evolution, should also be regarded as the foundations of existence and evolution of all the material world.
We live in an inherently metastable world, the world of relative equilibria and dissipative, nonequilibrium structures whose spontaneous origination is described by the irreversible process thermodynamics. From the standpoint of this thermodynamics, however, stable existence of what has already appeared is not a less intriguing problem, than origination of what is already existing. Namely, the thermodynamics accounts only for the variability of the material structures, whereas their conservatism is explained by the kinetic difficulties postulated as a consequence of only potential barriers (that is, eventually, by the existence of physical interaction forces); as a result, many really observed natural phenomena are moved outside the domain of action of the laws of thermodynamics.
The quantum electrodynamics explains origination of the physical interaction forces quite in the spirit of the thermodynamics of irreversible processes — by exchange of virtual, unobservable particles such as virtual photons in electromagnetic interactions. Yet the quantum electrodynamics considers the virtual particles as phantoms of a sort becoming physical reality because of high-energy processes (e.g., appearance of electron-positron pairs), whereas the thermodynamics does not stipulate reality by observability. In other words, if a system is a “black box”, its unobservable contents cannot be regarded, according to the quantum mechanical concepts, as a physical reality, which it is for thermodynamics.
In this sense, the koltsars give the situation that existed in physics at the turn of the century. They are systems to which the principles of thermodynamics are applicable generally, but which realize a most prominent feature of quantum behavior — the seemingly causeless ability to be arbitrarily long in dynamic nonequilibrium state.
5.2. Illegal postulate
The laws of thermodynamics are known to be correctly applicable only to strictly isolated systems consisting of ideal gas particles interacting only at direct instantaneous and absolutely elastic collisions9. If such ideal systems exchange substance and/or energy with their environment, this fact is easily accounted for by the irreversible process thermodynamics. It is assumed similarly that the real gas whose particles interact through some physical fields, can be both open or close system.
Yet as one can see for koltsars, the only introduction into a system isolated by definition of physical interaction forces causes an amazing paradox of feasibility of a process whose occurrence in the isolated system is forbidden by the second law of thermodynamics. The only reasonable way out of the situation is to recognize that the systems where stationary physical interaction forces exist, cannot be strictly isolated in principle10 .
In other words, this paradox can be solved theoretically only if the mechanism of origination of physical interaction forces in thermodynamic system is described only in terms of the thermodynamics itself. That is, if an answer is given to the question: What is “force” for thermodynamics?
If size and form of a body remain permanent indefinitely long, this means that the particles constituting the body are in potential wells owing to the action of stationary attraction and repulsion forces balancing each other. A piston positioned in the middle of an absolutely rigid closed cylinder filled with ideal gas at T > 0K (Fig.28, a) provides a thermodynamic model of such a system. At small shifts of the piston from the equilibrium state defined by the equality of gas pressures from the right and the left, a quasi-elastic force will occur directly proportional to the shift. In linear approximation, it is precisely in this manner that all the condensed phases behave resisting to extension and compression.
Thus, this model has in the state of mechanical equilibrium two pairs of stationary forces F1 and F2 making no work because the movement is zero. It is inferred as if logically from this fact that the very existence of these forces is in no way related to thermodynamics, that is, to mutual conversion of various forms of energy. Being equilibrium mechanically, this system is yet nonequilibrium thermodynamically because the gas producing the forces F1 is kept under pressure by the external forces F2 of unknown origin.
Generally speaking, the forces F2 can be produced in the same way as F1, that is, by purely thermodynamic means. Here one would have to introduce into the system additional pistons and cylinders, and so on ad infinitum (Fig.28, b); but in an infinitely large system the laws of thermodynamics have no sense. If an isolated system is finite-dimensional, one cannot make stationary acting forces appear in it by purely thermodynamic means.
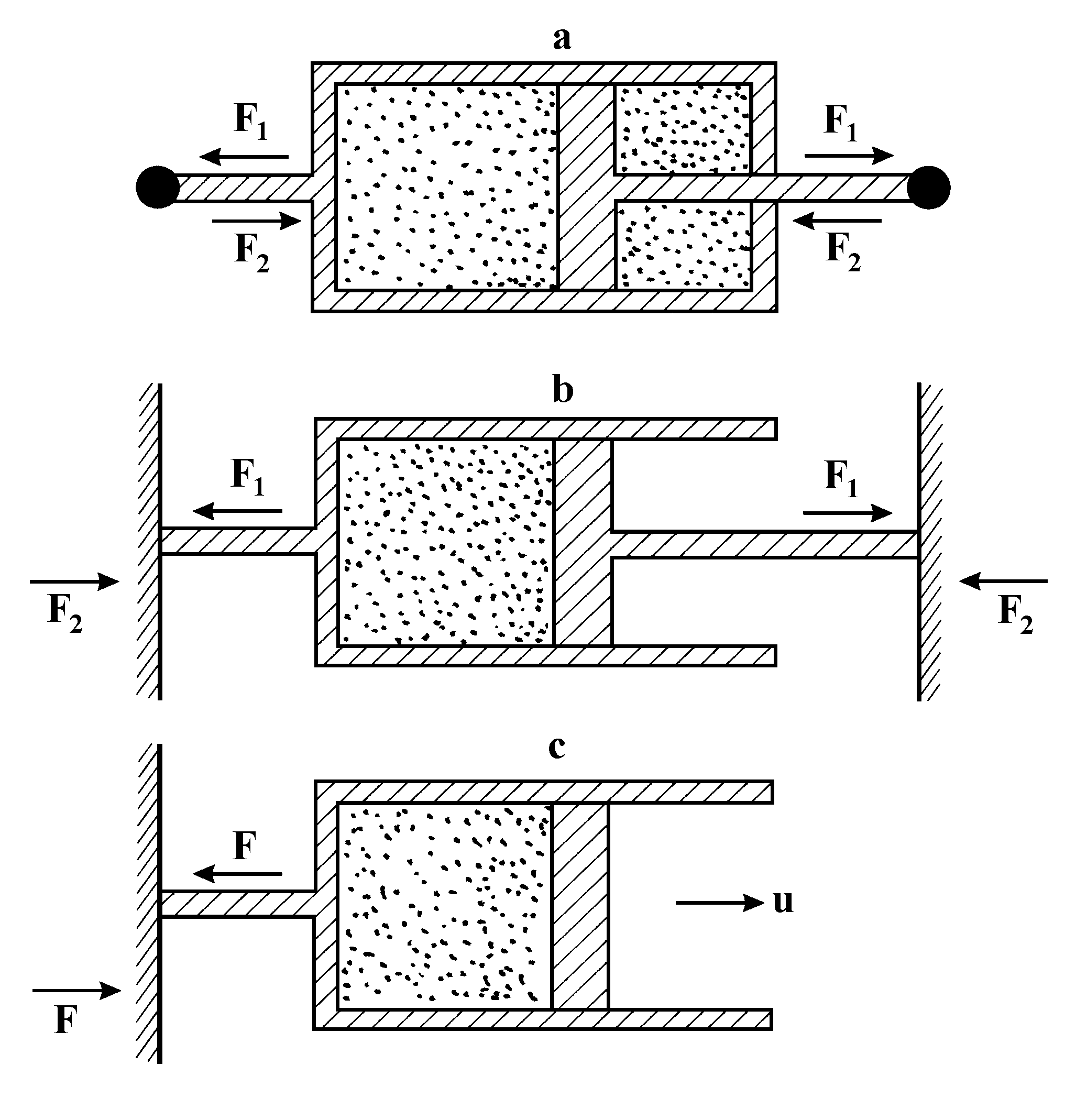
In other words, the quantum mechanical postulate about possible existence of stationary electronic orbits (eventually suggesting the possibility of phenomena such as superconductivity) is illegal from the thermodynamic point of view — it amounts to a postulate that stationary forces can exist in finite isolated systems. That is why the quantum mechanical phenomena are outside the scope of thermodynamic laws.
5.3. Origin of force
A stationary acting force can be created simply by thermodynamic means. For example, one can allow the ideal gas to expand ad infinitum in a cylinder with free piston (Fig.28, c). Cylinder shift here may be zero and, therefore, the work made by the force will also be zero. Simultaneously, the very existence of the force requires irreversible gas expansion associated with changes in system free energy.
The force appearing because of irreversible process can be stationary if the system is not isolated, but exchanges substance and/or energy with its environment. This phenomenon can be described by one of the so-called Knudsen effects observed in what is known as technical vacuum, that is, gases rarefied so that the length of particle mean free path becomes larger than the vessel linear dimensions, which is the case in many technical devices. The particles of “Knudsen gas” practically do not interact, but only collide elastically with the vessel walls exerting pressure on them.
Fig.28. Various ways of creating force in a thermodynamic system by its own means.
If one takes two vessels filled with the Knudsen gas and connects them by long and sufficiently thin capillaries (Fig.29), it is only natural that the pressures in the vessels will be equal, P1 = P2 if the walls with which the particles collide have equal temperatures T1=T2. If one vessel is constantly heated and another cooled, there will be stationary temperature difference between them D T = T1-T2, and their pressures cannot be equal.
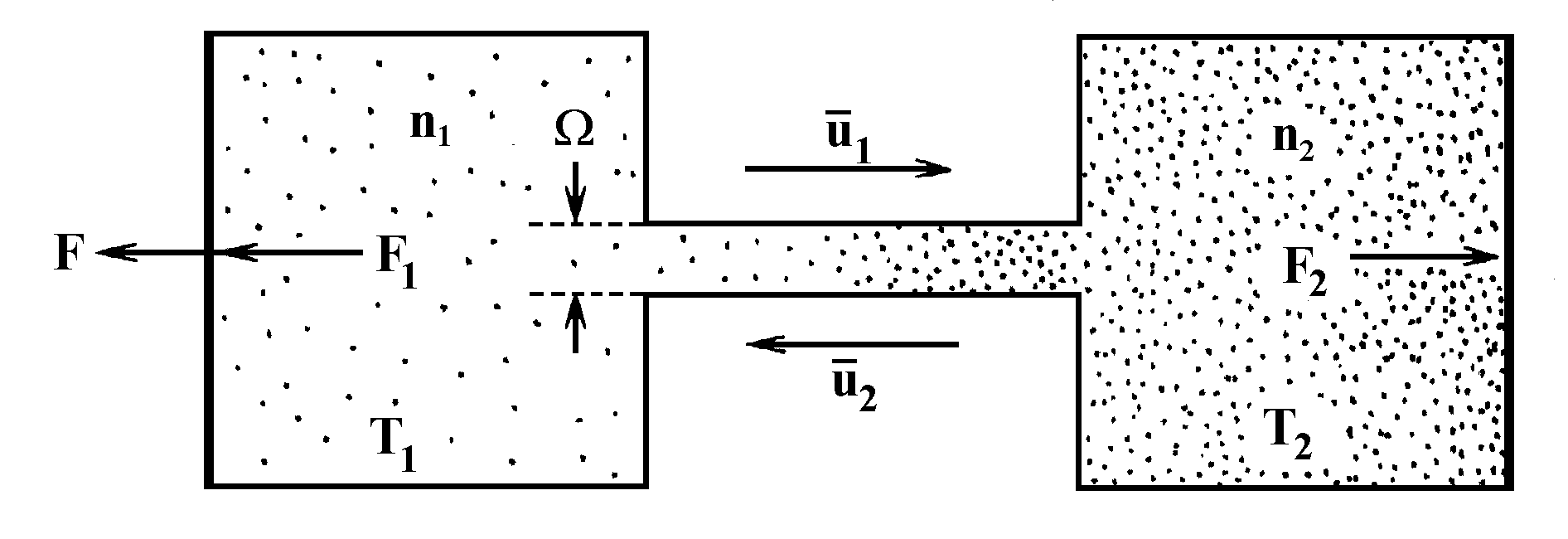
Namely, when the number of “fast” particles reflected by the “hot” wall of Vessel 1 and moving in a time unit through the capillary in one direction becomes precisely equal to that of “slow” particles reflected from the “cold” wall of Vessel 2 and moving in a time unit through the capillary in opposite direction, the system state will become stationary, that is, n1![]() 1= n2
1= n2![]() 2 where n1<n2 are volume concentrations of particles, and
2 where n1<n2 are volume concentrations of particles, and ![]() 1>
1>![]() 2 are their average velocities, so that stationary pressure difference D P=P1-P2 exists between Vessels 1 and 2, P1/P2 =
2 are their average velocities, so that stationary pressure difference D P=P1-P2 exists between Vessels 1 and 2, P1/P2 =![]() .
.
Fig.29. Creation of force in thermodynamic system by the Knudsen effect.
This and other Knudsen effects have been known for a long time, but nobody seems to have drawn attention to a fact that looks strange at first glance. If the capillary connecting Vessels 1 and 2 has cross section W , a force F1=W P1 acts upon the portion of Vessel 1 wall of area W that is against the capillary, and the same portion of Vessel 2 located against the opposite capillary end is subjected to force F2=W P2. As a result, the entire system is subjected to the following force that seems to be compensated by nothing:
![]() .
.
Actually, the third Newton law is not at all violated here. Assume that Vessel 1 is heated by a coil connected to a battery. Electrical power is high-potential. For the system to develop stationary force F, low-potential energy, i.e., heat must be removed continuously from Vessel 2. If the heat is radiated into the surrounding space as infrared quantums, something like photon propelling agent results, and nothing more (Fig.30). Nothing happens if we assume another way of creating heat flow causing the force F — action is equal to counteraction, and the momentum conservation law cannot be violated. This effect is only a good illustration of the well known L. Onsager’s mutuality relations — if a “force” (e.g., concentration gradient) causes “flow” (diffusion of substance), the flow of heat (energy, in general) produces force.
The heat flow required for occurrence of the force F can be readily evaluated by solving the following system of equations:

Allowing for F = F1 - F2, obtain
![]() , (9)
, (9)
where ![]() is some inherent constant of each particular thermodynamic system (velocity of relative motion of its component particles) depending only on the temperatures of heater and cooler, and on the mass of Knudsen gas particles, because
is some inherent constant of each particular thermodynamic system (velocity of relative motion of its component particles) depending only on the temperatures of heater and cooler, and on the mass of Knudsen gas particles, because ![]() ~
~ ![]() . In other words, the constant u0 is the inherent system standard velocity that can serve for objective measurement of velocities of any processes going on in the environment. Yet the system where no physical interaction forces exist, lacks “watch” of this kind.
. In other words, the constant u0 is the inherent system standard velocity that can serve for objective measurement of velocities of any processes going on in the environment. Yet the system where no physical interaction forces exist, lacks “watch” of this kind.
5.4. Force and work
Let free energy D E come over time D t to Vessel 1 (heater at temperature T1) creating thermal flow D Q/D t and, as a result, force F; and let heat be removed continuously from Vessel 2 (cooler at temperature T2). If under the action of force F and during this time the system moves rectilinearly and uniformly at distance D x, the energy balance condition will be as follows:
![]() , (10)
, (10)
where S is the entropy of production rate
![]() . (11)
. (11)
Substitution of (11) into (10) gives
![]()
and since (T1 - T2)/T1 = h is the efficiency of heat engine operating by the reversible Carnot cycle at heater and refrigerator temperatures, respectively, T1 and T2,
![]() . (12)
. (12)
This means that the free energy arriving at the system from outside cannot be transformed completely into the work directed to offsetting the external forces (uniform rectilinear motion of the entire system with velocity u = D x/D t in the presence of friction, for example), because a part of the energy must be used necessarily for creation of the same force (thermal flow D Q/D t). The same energy should be used for creating force also if the force acts, but produces no work (system motion is zero).
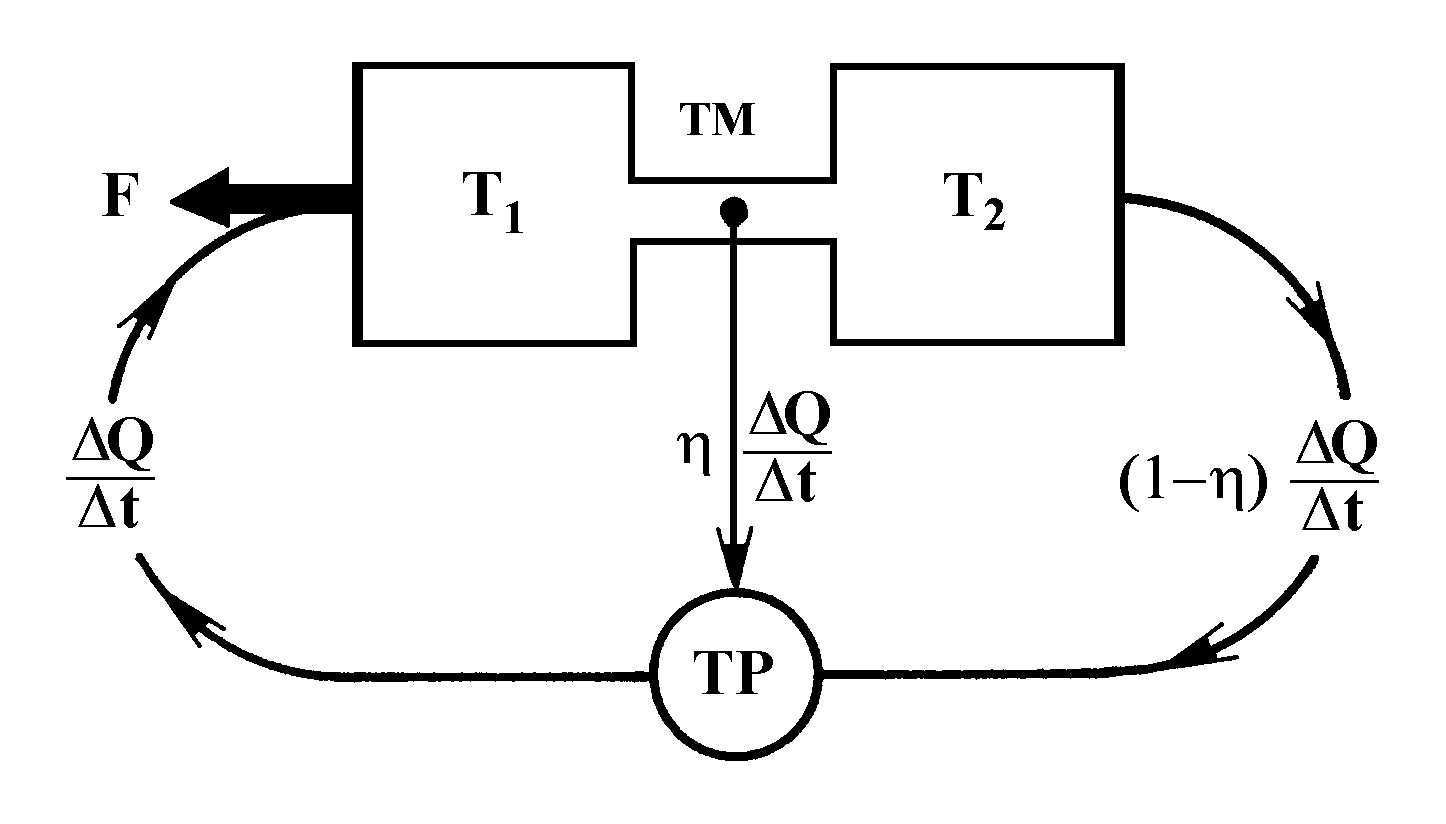
This conclusion, which is a direct consequence of the second principle of thermodynamics, requires some explanation. The thermal flow D Q/D t required for the force F to appear may be created by the refrigerating machine operating by the reverse reversible Carnot cycle (the so-called thermal pump) consuming exactly as much power as can be developed by a thermal machine operating by the direct reversible Carnot cycle between the same heater and refrigerator temperatures (Fig.31). Consequently, two systems can interact with force F if and only if they exchange energy whose flow, according to (9) and (12), is h Fu0 (Fig.32). If one speaks about exchange of particular virtual particles, and not about energy exchange in general, the mechanism of interaction as derived from the laws of thermodynamics does not differ in principle from the interaction mechanism as postulated by the quantum electrodynamics.
Fig.30. The Knudsen effect-generated force does not violate the momentum conservation law.
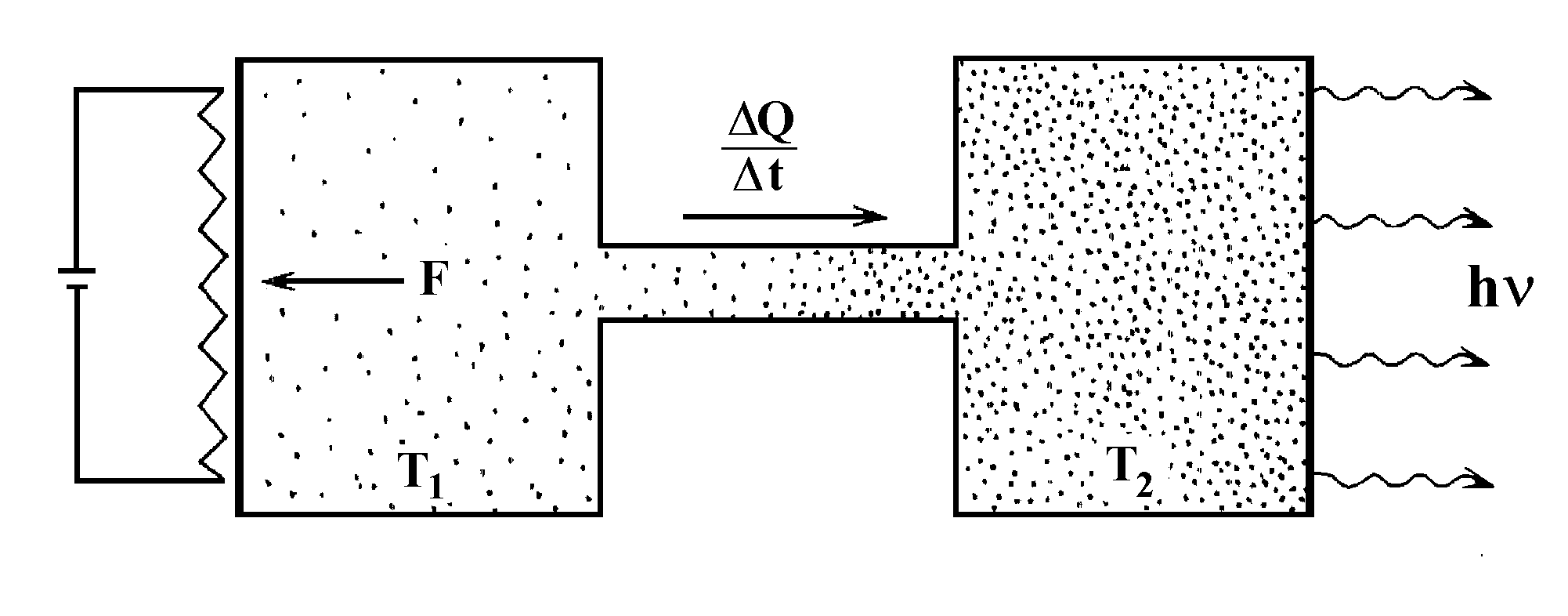
The thermodynamics, however, enables one to make another important conclusion of general nature: if a force F of no matter what nature acts upon the substance in the system, the latter, in principle, can by no means be regarded as isolated, because it is related to the environment by the energy flow D E/D t = h Fu0, the velocity standard for physical interactions u0 being taken equal to the light velocity in vacuum, c =3Ч 1010cm/sec11. Since for the thermodynamics, in contrast to the quantum electrodynamics, this flow is physically real in spite of nonobservability of virtual particles, koltsar-like effects in real systems must be quite usual. Also, these effects (escaping attention namely because of their universality and as if nonobservability) must be universal in nature, because any real body has gravitating mass and, therefore, is energy-related to all the bodies of the Universe, even if the sum of forces is zero. Stated differently, no isolated system exists in the nature in principle; this conclusion is the basic idea underlying the Kozyrev’s studies.
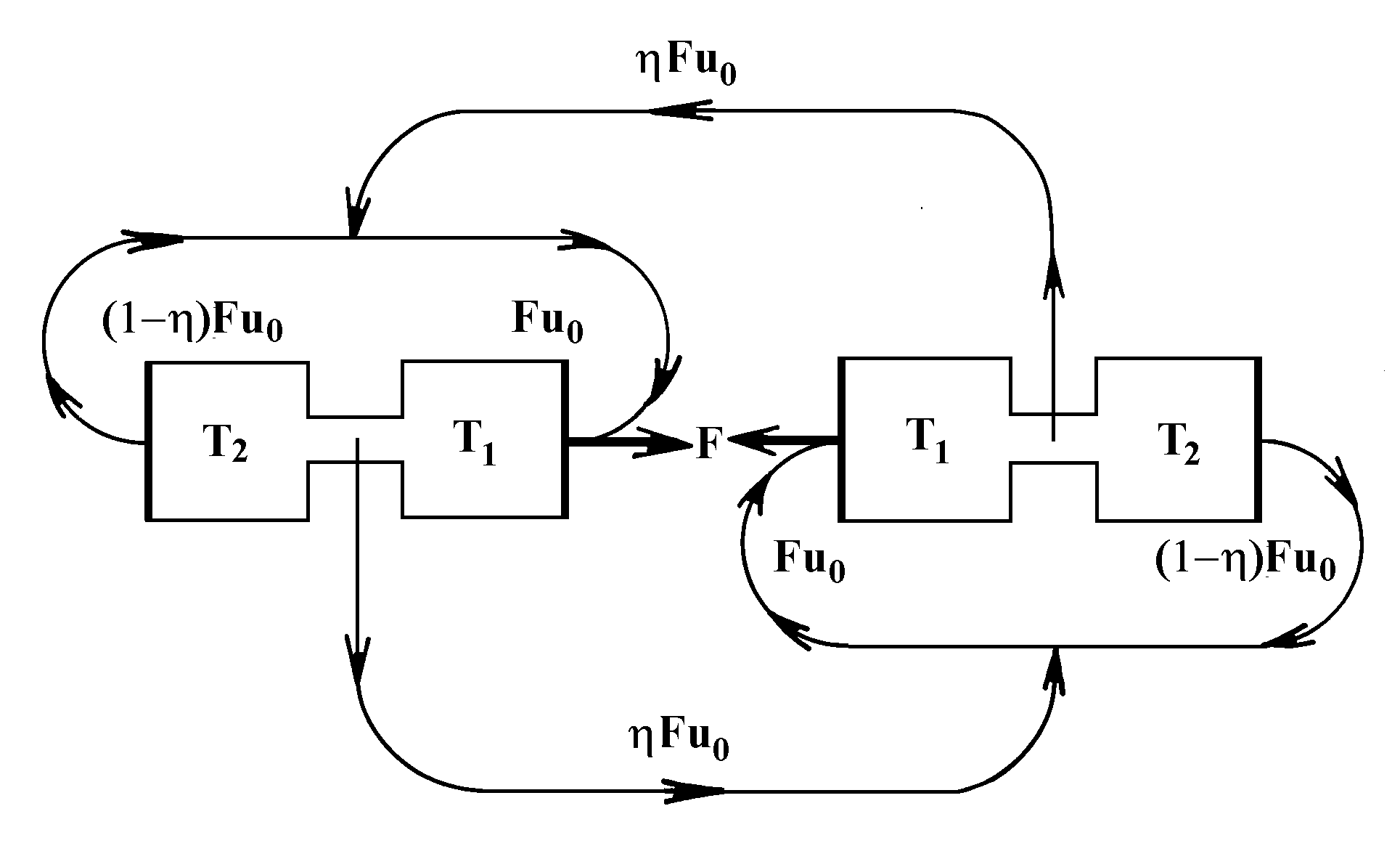
Fig.31. Only the moment of force appears in closed thermodynamic cycle (TM; thermal machine; TP; thermal pump).
6. Conclusion. Stars as cosmophysical koltsars
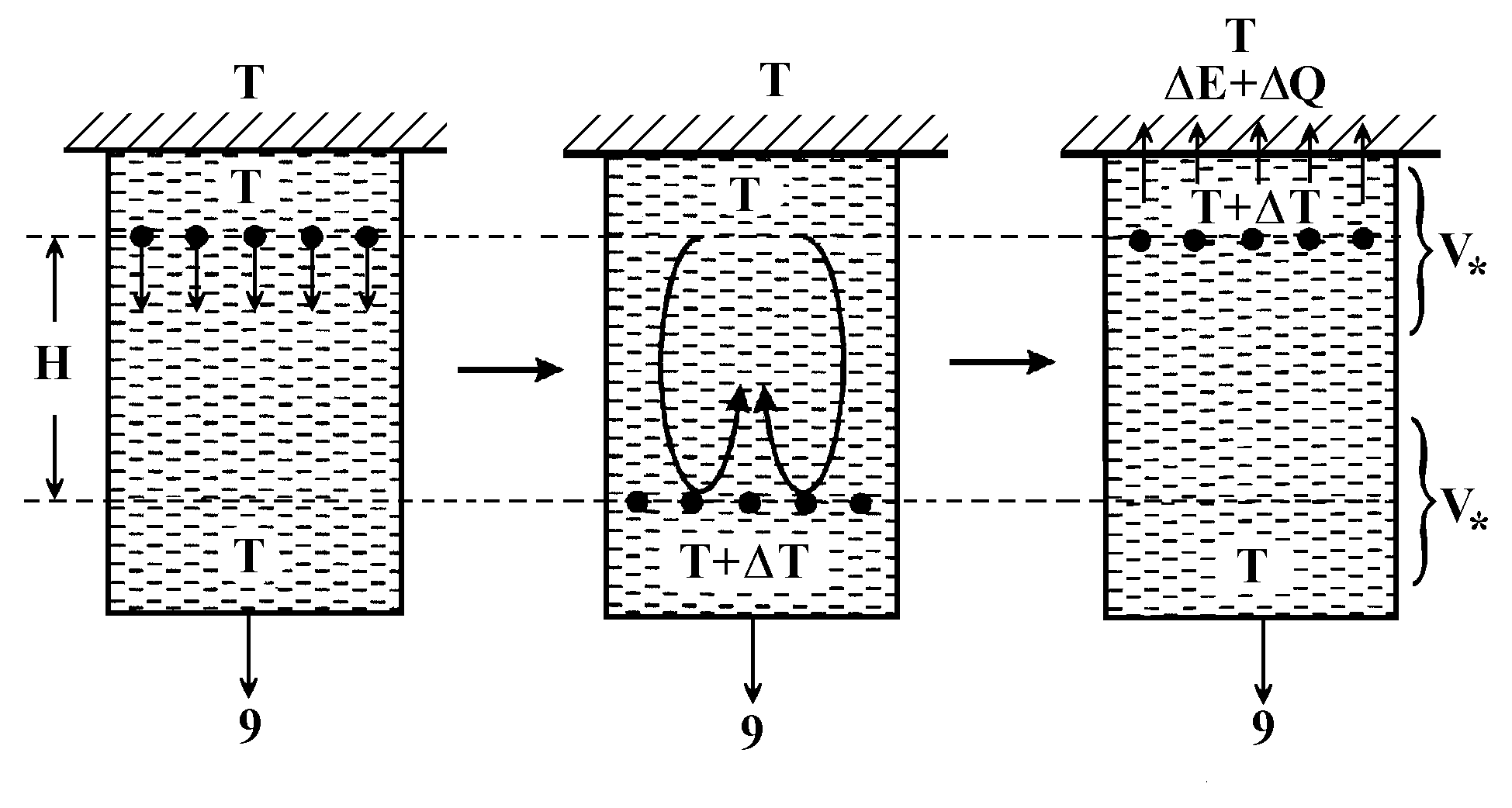
Thus, any real object is metastable, and has definite form and structure only as far as it continuously exchanges energy with the environment. If sometimes this energy still does not undergo any noticeable transformation and, therefore, remains unobservable, in the bistable systems it causes processes accompanied by useful work. If systems of this sort exist among nonquantum macroscopic objects (koltsars), it can be assumed that the Sun and the stars are such objects, and that, similar to Kozyrev initially assumed, the energy they produced has no direct relation with thermonuclear synthesis processes.
Consider for the beginning the following simplistic model: let liquid of density r l be placed into a vessel of height H and volume Vl at temperature T equal to that of the environment; place solid balls of a material with density r S > r l and of total volume VS<Vl into the upper part of vessel (Fig.33). If under the action of the gravity force the balls go down to depth H, the system passes into one of the possible stationary states, and the potential energy of the balls transforms into heat
![]()
thus, increasing the temperature of the liquid of heat capacity Cl in the lower part of the vessel by
![]() ,
,
and decreasing its density by
![]()
with b l for the liquid thermal expansion coefficient. As a result, a convective flow appears carrying along the balls up to height H, the system passing into the second possible stationary state.
Fig.32. The interacting thermodynamic systems must exchange energy by exchanging angular momentum (in real systems, the interaction forces cannot be strictly central, which implies violation of spatial symmetry).
Disregarding the fact that the interacting bodies (here, the Earth and the vessel with liquid and balls) exchange energy, and assuming that the vessel is an isolated system, the convective flow energy
![]()
must be exactly equal to the energy imparted to the liquid by the balls going down to depth H, that is, D E=D Q. The energy conservation law, however, imposes no restrictions on the relationship between temperature decrease of liquid density and the amount of heat imparted to it. Therefore, the convective flow energy under certain combination of system parameters may, in principle, exceed the initially liberated potential energy transforming into heat. To put it another way, the condition D E>D Q may be realized, entailing no violation of the conservation law, because the system in actual fact is open, and not isolated.
Thus, if the following inequality
![]()
holds, the liquid in vessel can transform the environmental energy into that of thermal radiation. Interestingly, the balls introduced initially into the model under consideration proved finally to be unnecessary — the gravity field as if heats the liquid from below causing convective flows, the liberated energy being radiated from above as heat, that is, as infrared electromagnetic radiation.
Now, instead of the vessel with liquid, if we consider a liquid sphere of radius R and mass M that has formed under the action of its natural gravity forces, and assume that R=H, and if the inequality
![]()
with g for the gravitational constant, is also satisfied, we see that the sphere will radiate energy like a star. True, for liquids this inequality cannot be realized under any condition; but taking into account that for gases b ~ 1/T and C~T, obtain the final self-luminosity condition for the celestial bodies:
![]() ,
,
where e is some constant factor. Indeed, as was established by Kozyrev, the following condition
![]()
is satisfied for the main sequence stars, the giants and the supergiants (Fig.34).
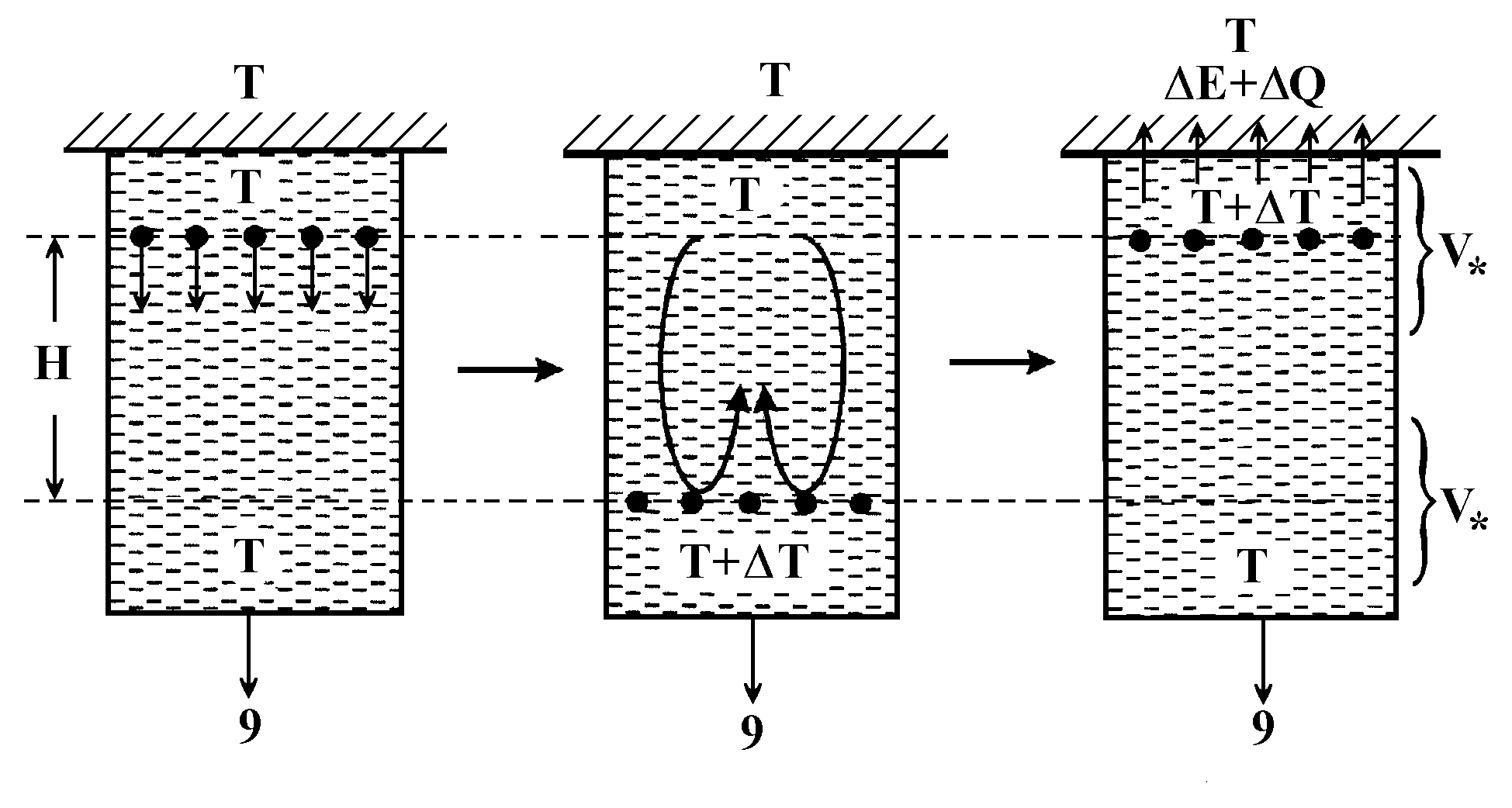
Fig.33. Calculation of energy production by star convective model (cosmophysical koltsar).
This fact implies that the star energy comes mainly from the energy introduced by the gravity forces combining all the bodies of the Universe into one, rather than from thermonuclear synthesis. In other words, the stars are nonlocal cosmophysical koltsars; as for thermonuclear synthesis reactions, they are side processes realized only in special cases and under special conditions, but not going on necessarily. Possibly, this accounts for the observed deficiency of solar neutrinos.
The works of Kozyrev were not understood and received by his contemporaries (even today they are met mostly with scepticism) for the reasons that bear not upon the gist of the matter. First, they were much ahead of their time and fell on unprepared soil. Second, they proved to be terminologically poor, which is also due to their extremely pioneering character. Third, they appeared in the country where a deviation from any (even scientific) paradigm was regarded, at best, as psychic aberration, or, at worst, as treason.
The attitude towards the Kozyrev’s heritage should be neither critical, non dogmatic, but rather that of respect and creativity, trying to gain insight into its logic and to identify its relations with the international scientific mainstream. It should be regarded as a road sign to new experimental and theoretical studies.
2
It seems not accidental that some contemporary attempts to reproduce the original Kozyrev’s experiments are related namely to the physical vacuum theories (Akimov, Pugach 1992).3
For some reason, till now nobody paid attention to the fact that the classical thermodynamics, which is, due to methodical use of the notion of “isolated system,” basically a local theory, has led eventually in complete compliance with the Bell theorem to the statistical, and later to the quantum mechanics describing adequately the dead microworld in terms of the probability theory; whereas the nonlinear thermodynamics, which appeared from the need to give an adequate description of the determinate phenomena of life, came into contact with manifestations of nonlocality, e.g., space correlation of processes in reactions of the Belousov-Zhabotinsky type. Here one has to take into consideration that the notion of “locality” in terms of the irreversible process thermodynamics carries the sense opposite to its physical counterpart.4
This result may be checked qualitatively in the following way. If the barometric formula is expanded into a power series, it will turn out that D P ~5
The term “lifetime” is to the point and can be used without inverted commas, because, as will be seen below, the koltsar may be regarded as a living nonbiological structure existing at the expense of energy exchange with its environment.6
Appearance of energy in the barometric formula has no effect upon the matter — if the vertical molecule distribution is disregarded, D P only grows dramatically (Dmitriev 1991). Moreover, precisely this formula was used to prove the impossibility of the koltsar effect (Rusanov 1991). The same publication described the osmotic koltsar and proved that it cannot operate. The author’s error is that he assumed that molecular motions are controlled by chemical potentials rather than forces, and, therefore, obtained the desired negative result.7
A.N. Sharova, L.Sh. Gelis, Ya.I. Vertsimakha, N.E. Nevessky and V.A. Fedorov participated in the experimental part of the study.8
One cannot rule out the possibility of the koltsar effect being related somehow to the well-known phenomenon of high-temperature superconductivity, because, like the koltsars, the high-temperature superconductors feature highly organized laminar multi-component structure.9
It might be well to note that uncontrollable use of notions that are explicitly or implicitly based on the notion of “infinity” harbors the danger of paradoxes. According to a strict definition, an infinitely large value is an evergrowing one that never becomes equal to something definite. It is, however, usually implied that it is just a very large value that cannot be measured for purely technical reasons.If one assumes that particles collide instantaneously, that is, with infinitely high velocity, they never would and will be at finite distances from one another, and should always constitute a whole existing outside time and space. The same would be concluded if interactions are assumed to propagate instantly, that is, with infinite velocity. Stated differently, the notion of “instantaneity,” which is equivalent to “infiniteness,” introduces implicitly into mechanics the notion of nonlocality incompatible with the existence of isolated systems and conservation laws.
10
In the light of the above footnote, this means that any real physical system is nonlocal in principle and that nonlocality is a fundamental property of nature. Consistent use of the locality principle without which scientific description of nature is impossible, makes behavior of some real objects (koltsars, in particular) either inexplicable, or (as is the case in the quantum mechanics) requiring additional postulates that contradict implicitly the corresponding postulates of the classical theory (e.g., deprive it of determinism).11
Having denoted the light speed in vacuum by c1, Kozyrev introduced the constant c2 = h c1 where h has the order of weak interaction constant, that is, h ~ a 2 = (1/137)2 ~ 5.3× 10-5. To this constant Kozyrev relates all self-organizing and evolutionary processes in the animate and inanimate worlds that are accompanied by macroscopic violations of spatial symmetry and nonlocality effects.
REFERENCES
AKIMOV A.E. and PUGACH A.F. (1992). On the Possibility of Detecting Torsion Waves by Astronomic Methods. Preprint 25. CISE VENT. Moscow (in Russian).
DMITRIEV V.M. (1991). Amazing osmosis. Khimiya i Zhizn’ (Chemistry and Life), N.8, pp.70-71 (in Russian).
KOZYREV N.A. (1948). Sources of star energy and theory of star internal structure. Part I. Izvestiya Krymskoi Astrofizicheskoi Observatorii (Bulletin of the Crimean Astrophysical Observatory), V.2, pp.3-43 (in Russian).
KOZYREV N.A. (1951). Theory of star internal structure and star energy sources. Part II. Izvestiya Krymskoi astrofizicheskoi observatorii (Bulletin of the Crimean Astrophysical Observatory), V.6, pp.54-83 (in Russian).
KOZYREV N.A. (1958). Causal or Nonsymmetrical Mechanics in Linear Approximation. Pulkovo (in Russian).
MIROSHNICHENKO L.I. (1981). Solar Activity and the Earth. Moscow (in Russian).
PRIGOGINE I. and STENGERS I. (1984). Order out of Chaos. Man’s New Dialogue with Nature. Heinemann. London.
RUSANOV A.I. (1991). Osmosis in terrestrial environment. Khimiya i Zhizn’ (Chemistry and Life), N.8, pp.71-72 (in Russian).
TEMUR’YANTTS N.A., VLADIMIRSKY B.M. and TISHKIN O.G (1992). Super-Low-Frequency Electromagnetic Signals in the Biological World. Kiev (in Russian).
UDAL’TSOVA N.V., KOLOMBET V.A. and SHNOL’ S.E. (1987). Possible Cosmophysical Dependence of Macroscopic Fluctuations in Different Processes. Pushchino (in Russian).
VLADIMIRSKY B.M. (1990). Macroscopic fluctuations, solar-terrestrial relationships and methodological issues of precise measurements. Izvestiya Krymskoi Astroizicheskoi Observatorii (Bulletin of the Crimean Astrophysical Observatory), V.82, pp.161-172 (in Russian).
ZHVIRBLIS V.E. (1989). On reproducibility of heliobiological experiments. In: Problemy Kosmicheskoi Biologii. Biofizicheskie i Klinichecskie Aspecty Geliobiologii (Problems in Space Biology. Biophysical and Clinical Aspects of Heliobiology). Leningrad, V.65, pp.145-160 (in Russian).
ZHVIRBLIS V.E. (1991). Lazarev’s “Koltsar” — the First Example of Artificial Dynamic Dissipative Structure. Preprint 1. CISE VENT. Moscow.
ZHVIRBLIS V.E. (1992). Device for Recording Electron Work Function Fluctuations. Patent of the Russian Federation N.2006988 (in Russian).
ZHVIRBLIS V.E. (1993). Phenomenological Description and Experimental Study of Some Koltsars. Preprint 33. CISE VENT. Moscow (in Russian).
ZHVIRBLIS V.E. (1994). Design of the space of life. Mendeleev Chemistry Journal, V.38, N.6, pp.107-117 (in Russian).