Успехи современной биологии, 2003, том 123, № 2, с. 115-137.
© П.В.Фурсова, А.П.Левич, В.Л.Алексеев
УДК 57.02.001.57
ЭКСТРЕМАЛЬНЫЕ ПРИНЦИПЫ В МАТЕМАТИЧЕСКОЙ БИОЛОГИИ
П.В.Фурсова, А.П.Левич, В.Л.Алексеев
Московский государственный университет им. М.В.Ломоносова, биологический факультет, Москва
ВВЕДЕНИЕ
Математическое моделирование биологических процессов – достаточно обширная область исследования и по выбору объектов моделирования, и по набору методов, и по спектру решаемых задач. Предлагаемый читателю обзор не претендует на охват всех аспектов моделирования. Внимание авторов обращено на методы, основывающиеся на экстремальных принципах биологии.
Модели каждого из методов, безусловно, обладают своими достоинствами и недостатками. Так, дифференциальные или разностные уравнения позволяют описывать динамику процессов в режиме реального времени, тогда как вариационные методы, как правило, предсказывают лишь конечное стационарное состояние сообщества. Но на пути имитаций с помощью уравнений возникают трудности как принципиального, так и технического характера. Принципиальная трудность состоит в том, что не существует систематических правил вывода самих уравнений. Процедуры их составления основываются на полуэмпирических закономерностях, правдоподобных рассуждениях, аналогиях и искусстве модельера. Технические трудности связаны с высокой размерностью задач по моделированию сообществ. Для существенно многовидовых сообществ, потребляющих многочисленные ресурсы, требуется подбор сотен коэффициентов и анализ систем из десятков уравнений. (Если изучается сообщество из w групп организмов, потребляющих m ресурсов, то соответствующая система дифференциальных уравнений должна содержать, по крайней мере, w + mw + m уравнений с 2w + 4mw параметрами, требующими идентификации.) Обычные приемы снижения числа переменных – их агрегирование или учет только доминирующих групп организмов – непригодны во многих задачах экологии. С течением времени существенную роль начинают играть редкие и малочисленные виды, которые, тем самым, следует включать в число переменных на начальных этапах моделирования. Агрегация переменных может нивелировать результаты управления функционированием сообществ. При работе с системами из десятков и более дифференциальных уравнений оказывается, что проследить причинные связи (для отладки, исключения ошибок, интерпретаций) в системе уравнений также сложно, как и в реальной экосистеме. В конце концов, оказывается, что мы не можем узнать, чему обязаны полученными результатами: реальному положению вещей, ошибкам в исходных данных, недочетам алгоритма или еще чему-либо. Модели, основанные на экстремальных принципах, как правило, преодолевают "проклятие размерности", но сохраняют произвол в выборе самих исходных принципов.
Согласно экстремальным принципам в реальности осуществляются лишь некоторые состояния системы, а именно, состояния с экстремальным значением числовой функции или функционала, называемых “целевой функцией”, которая определяет развитие природной системы. Широкое применение экстремальные принципы получили в физике, механике, термодинамике, экономике, теории управления. В биологии вопрос о “целевой функции” стал более популярен с распространением эволюционного мышления в противовес статическому видению мира [54]. В настоящем обзоре достаточно подробно представлены следующие экстремальные принципы: принцип минимума общего осмотического давления [46]; принцип максимальной общей скорости биохимической реакции [55]; принцип минимизации поверхностной энергии в развитии эмбриона [30]; принцип оптимальной конструкции [18]; принцип максимума жизненного репродуктивного успеха особи [21, 47]; принцип максимальной биомассы потомства [3]; принцип выживания [22]; принцип максимизации репродуктивных усилий [56]; принцип максимальной неожиданности протекания эволюции [1]. Описан вывод логистического уравнения роста популяции, основанный на требовании экстремальности функционала действия [52]. Представлено применение принципа максимума Понтрягина в биоэкономической модели [27]. В работе содержится принцип стационарного состояния открытых систем [17]; принцип максимального разнообразия [36]; принцип максимальной обобщенной энтропии [4]; принцип минимума потребления лимитирующего вещества [15]; принцип максимума мальтузианского параметра [19]; принцип максимума использованной энергии [16]; принцип максимального суммарного дыхания [51]. Описаны экстремальные свойства сообщества с горизонтальной структурой [20]. В основе, так называемых, моделей динамической структуры, представленных в работе, лежит максимизация скорости изменения общего потока энергии через систему, асценденции, эмержентности, эксергии, косвенных эффектов, индекса зрелости [31, 32, 41, 42, 43]. Использование термодинамики для решения проблем эволюции отражено в принципе наименьшей диссипации энергии и принципе наискорейшего спуска [2].
Обзор не претендует на полное освещение всех возможных применений экстремальных принципов в биологии, и тем более на подробное описание, поэтому лишь перечислим еще некоторые из них: максимальное рассеяние энергии [49, 45, 38], максимизация биомассы [37], максимум устойчивости органического вещества [53].
ПРИНЦИП МИНИМУМА ОБЩЕГО ОСМОТИЧЕСКОГО ДАВЛЕНИЯ
С.Шустер и Р.Гейнрих [46] применяли метод условной экстремизации при изучении стационарного течения биохимических реакций. Они принимают, что общее осмотическое давление промежуточных продуктов в реакции можно записать в виде
![]() ,
,
где ![]() и
и ![]() обозначают, соответственно, концентрацию и коэффициент осмотического давления i-го промежуточного продукта реакции (зависимость
обозначают, соответственно, концентрацию и коэффициент осмотического давления i-го промежуточного продукта реакции (зависимость ![]() только от
только от ![]() является упрощающим предположением). Естественно, что осмотическое давление в клетке не может превосходить некоторой критической величины. Поэтому авторы считают, что при стационарном течении реакции, при котором все
является упрощающим предположением). Естественно, что осмотическое давление в клетке не может превосходить некоторой критической величины. Поэтому авторы считают, что при стационарном течении реакции, при котором все ![]() не зависят от времени,
не зависят от времени, ![]() должно принимать минимальное значение при ограничениях
должно принимать минимальное значение при ограничениях
![]() .
.
Здесь ![]() – некоторые равновесные константы реакции,
– некоторые равновесные константы реакции, ![]() – элементы стехиометрической матрицы реакционной системы. Ограничения – неравенства имеют смысл положительности скорости всех промежуточных реакций. Таким образом, при стационарном течении реакции, концентрации промежуточных продуктов
– элементы стехиометрической матрицы реакционной системы. Ограничения – неравенства имеют смысл положительности скорости всех промежуточных реакций. Таким образом, при стационарном течении реакции, концентрации промежуточных продуктов ![]() , находятся как решения следующей задачи
, находятся как решения следующей задачи
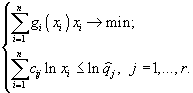 (1)
(1)
В качестве примера С.Шустер и Р.Гейнрих рассматривают реакции метаболизма эритроцитов человека [46]. Поскольку эти реакции довольно сложные, то авторы получают лишь общую качественную картину решения задачи (1) в этом случае. Они отмечают, что эта картина согласуется с известными экспериментальными данными о метаболизме эритроцитов.
ПРИНЦИП МАКСИМАЛЬНОЙ ОБЩЕЙ СКОРОСТИ БИОХИМИЧЕСКОЙ РЕАКЦИИ
Еще одно приложение метода условной оптимизации к исследованию биохимических реакций демонстрируют Т.Вильгельм с соавторами [55]. Они рассматривают биохимическую реакцию, состоящую из n элементарных шагов. Состояние реакции авторы характеризуют вектором ![]() , где
, где ![]() – константа скорости прямой (обратной) реакции i-го шага,
– константа скорости прямой (обратной) реакции i-го шага, ![]() . Авторы вводят гипотезу, что при стационарном течении общая скорость реакции
. Авторы вводят гипотезу, что при стационарном течении общая скорость реакции ![]() должна быть максимальна при ограничениях на величину
должна быть максимальна при ограничениях на величину ![]() и при фиксированной константе равновесия реакции
и при фиксированной константе равновесия реакции ![]() . Таким образом, для описания стационарного течения реакции авторы используют экстремальную задачу
. Таким образом, для описания стационарного течения реакции авторы используют экстремальную задачу
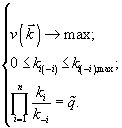 (2)
(2)
Здесь ![]() и
и ![]() предполагаются известными параметрами задачи.
предполагаются известными параметрами задачи.
Авторы рассматривают несколько конкретных примеров, для которых результаты решения (2) согласуются с экспериментальными данными.
ПРИНЦИП МИНИМИЗАЦИИ ПОВЕРХНОСТНОЙ ЭНЕРГИИ В РАЗВИТИИ ЭМБРИОНА
Н.Гоэл с соавторами [30] при помощи задачи на условный экстремум изучают один из ранних этапов развития эмбриона млекопитающих – процесс перехода между ранней и поздней морулой. Этот переход достаточно хорошо изучен. Он включает 4 этапа: клеточное деление, компактификацию, переферическое склеивание и появление внутренних клеток (интернализация). Компактификация состоит в том, что контактирующие части поверхностей клеток, возникших после деления и имеющих форму сфер, увеличиваются до такого состояния, что все внутриклеточное пространство, необходимо существующее между близко упакованными сферами, удаляется (путем индивидуальных деформаций первоначально сферических клеток), в то время как целый эмбрион приобретает сферическую форму. При этом компактификация идет именно до такого состояния, когда эмбрион приобретает форму сферы и не далее.
Для объяснения компактификации и интернализации авторы предлагают гипотезу, что клеточная конфигурация строится таким образом, что она минимизирует поверхностную энергию ![]() (
(![]() – число клеток в конфигурации) при условии фиксированного общего объема. Таким образом, получается задача на условный экстремум
– число клеток в конфигурации) при условии фиксированного общего объема. Таким образом, получается задача на условный экстремум
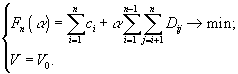 (3)
(3)
В выражении для поверхностной энергии ![]() в (3)
в (3) ![]() – площадь поверхности стенок i-ой клетки, находящихся в контакте только с окружающей средой (и не имеющих точек касания с другими клетками) и
– площадь поверхности стенок i-ой клетки, находящихся в контакте только с окружающей средой (и не имеющих точек касания с другими клетками) и ![]() – общая площадь стенок i-ой и j-ой клеток, V – объем. Параметр
– общая площадь стенок i-ой и j-ой клеток, V – объем. Параметр ![]() задается как некий весовой фактор для межклеточных поверхностей, отличающий их от стенок клеток, имеющих контакты только с внешней средой (для таких стенок параметр
задается как некий весовой фактор для межклеточных поверхностей, отличающий их от стенок клеток, имеющих контакты только с внешней средой (для таких стенок параметр ![]() считается равным единице).
считается равным единице).
Задача (3) сложна для аналитического решения. Поэтому авторы пытались решить ее численно для случая плоских (двухмерных) клеток и для некоторых специальных случаев трехмерных клеток [35]. Оказывается, что при ![]() минимум в (3) реализует конфигурация, при которой все клетки имеют форму кругов (или сфер) и каждая касается соседей только в одной точке, а при
минимум в (3) реализует конфигурация, при которой все клетки имеют форму кругов (или сфер) и каждая касается соседей только в одной точке, а при ![]() минимум в (3) реализует конфигурация, при которой каждая клетка деформируется таким образом, что внутриклеточные пространства исчезают, а вся совокупность клеток приобретает форму сферы (круга в двухмерном случае). Таким образом, по мнению авторов, процесс компактификации можно описать путем уменьшения
минимум в (3) реализует конфигурация, при которой каждая клетка деформируется таким образом, что внутриклеточные пространства исчезают, а вся совокупность клеток приобретает форму сферы (круга в двухмерном случае). Таким образом, по мнению авторов, процесс компактификации можно описать путем уменьшения ![]() в (1.5) с 2 до 0. (Физический механизм этого уменьшения авторы трактуют, связывая
в (1.5) с 2 до 0. (Физический механизм этого уменьшения авторы трактуют, связывая ![]() с концентрацией
с концентрацией ![]() ионов в окружающей эмбрион среде. Из экспериментальных наблюдений известно, что при компактификации эта концентрация уменьшается.)
ионов в окружающей эмбрион среде. Из экспериментальных наблюдений известно, что при компактификации эта концентрация уменьшается.)
Другим важным результатом численного исследования (3) оказывается тот факт, что при достаточно большом числе клеток ![]() конфигурация с внутренними клетками имеет меньшую энергию
конфигурация с внутренними клетками имеет меньшую энергию ![]() чем конфигурация без них (независимо от
чем конфигурация без них (независимо от ![]() ). По мнению авторов, это может служить возможным объяснением интернализации.
). По мнению авторов, это может служить возможным объяснением интернализации.
Таким образом, по мнению авторов, модель (3) достаточно адекватно описывает некоторые сложные процессы происходящие при развитии эмбриона млекопитающих.
ПРИНЦИП ОПТИМАЛЬНОЙ КОНСТРУКЦИИ
Вопрос об оптимальности в биологии подробно изучался Р.Розеном [18]. Основой для его рассуждений является естественный отбор, в результате которого живые организмы приобретают признаки, оптимальные для данных условий, т.е. такие, которые не скажутся отрицательно на их способности конкурировать с соперниками. Основная гипотеза заключается в том, что организмы, обладающие биологической структурой, оптимальной в отношении естественного отбора, оптимальны также и в том смысле, что они минимизируют некоторую оценочную функцию (принцип оптимальной конструкции). Эта функция определяется исходя из основных характеристик окружающей среды.
Одним из приложений принципа оптимальной конструкции является моделирование кровеносной системы. Рассмотрена задача нахождения оптимального угла отклонения боковой ветви от основного ствола. Радиусы ствола и ответвления считаются известными: r0 и r1. В качестве оценочной функции выбирается сопротивление кровеносной системы, которое согласно принципу оптимальности должно быть минимальным (участок АДС на рис. 1).
Зависимость полного сопротивления RT участка АДС от угла ответвления q выглядит следующим образом
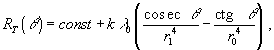
где k – коэффициент пропорциональности, зависящий от вязкости и плотности жидкости; λ0 – длина отрезка СВ.
Дифференцирование функции RT(q ) по q и приравнивание результата нулю дает оптимальное значение угла
![]() .
.
Следующим шагом является рассмотрение разветвления сосудов (рис. 2). Оценочной функцией здесь выступает мощность, рассеиваемая при движении жидкости
![]() ,
,
где f – поток жидкости; K – постоянный коэффициент пропорциональности; RT – полное сопротивление; V – объем изучаемого участка.
Полученные оптимальные значения углов разветвления сравнивали с реальными углами системы кровеносных сосудов кошки и получили хорошие совпадения.
Развитие описанных методов позволяет найти оптимальный радиус отходящей ветви, радиус аорты, а также общее число капилляров, в предположении, что каждый сосуд (кроме аорты) образуется в результате разветвления более крупного сосуда. Полученные результаты хорошо совпадают с эмпирическими данными.
На основании принципа оптимальной конструкции Р.Розеном также была высказана гипотеза о том, что аллометрические соотношения, имеющие место в живой природе, могут быть выведены из условия минимизации некоторого функционала, и показывается, как эта гипотеза может объяснить теорию трансформации д'Арси Томпсона.
ОПТИМАЛЬНАЯ ЖИЗНЕННАЯ СТРАТЕГИЯ РАСПРЕДЕЛЕНИЯ ЭНЕРГЕТИЧЕСКИХ РЕСУРСОВ ИНДИВИДА
Принцип максимума жизненного репродуктивного успеха особи. Методы вариационного исчисления применяются в эволюционной экологии. Оптимизационный подход основан на предположении, что в процессе эволюции вида при заданных внешних условиях и физиологических ограничениях оптимизируется удельная скорость роста популяции, которая выступает в качестве критерия дарвиновской приспособленности. Это позволяет формулировать задачу эволюционной оптимизации жизненного цикла в терминах математической теории оптимального управления как задачу нахождения оптимальных жизненных стратегий распределения энергетических ресурсов индивида между ростом, размножением, добыванием пищи, защитой от неблагоприятных влияний внешней среды и репарацией (вклад энергии в репарацию означает вклад в “будущее выживание”) [21].
Общая оптимизационная задача выглядит следующим образом [47]
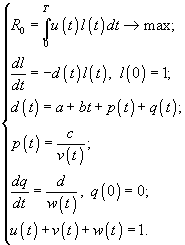
Здесь u(t) – часть энергии, затраченная на воспроизведение; l(t) – функция выживания; d(t) – смертность, включающая четыре компоненты: две контролируемые и две неконтролируемые индивидом; a – постоянная часть неконтролируемой (внешней) смертности; bt – неконтролируемая смертность, возрастающая с возрастом со скоростью b; p(t) – текущий уровень смертности, регулируемый вкладом энергии v(t) – (часть энергии направленная на выживание); c ³ 0, c = const; q(t) – скорость старения, контролируемая вкладом энергии в репарацию w(t). Последнее равенство означает, что никакие другие нужды организма, кроме воспроизводства, выживания и репарации, не включаются в модель.
Целевым функционалом является жизненный репродуктивный успех особи. Этот функционал применим в тех случаях, когда численность популяции меняется не слишком быстро, иначе, правильнее было бы использовать удельную скорость роста численности популяции μ, получаемую из уравнения Эйлера-Лотки ![]() [21]. Однако, рассматривая множитель
[21]. Однако, рассматривая множитель ![]() как часть выживания, можно считать, что оптимизация удельной скорости μ эквивалентна оптимизации R0 в присутствии дополнительной константы внешней смертности μ [47].
как часть выживания, можно считать, что оптимизация удельной скорости μ эквивалентна оптимизации R0 в присутствии дополнительной константы внешней смертности μ [47].
Изучение модели идет по пути рассмотрения частных случаев. Задача о распределении энергии между воспроизведением и выживанием описывается исходной системой при условии, что w(t) º
0. Вариационная задача решается применением принципа максимума Понтрягина. Оптимальная стратегия задается выражением: ![]() , где функция x(t) – решение уравнения
, где функция x(t) – решение уравнения
![]()
Численные решения этих уравнений позволяют наблюдать зависимость стратегии от параметров.
Предположение о неопределенности максимальной продолжительности жизни Т (Т = ¥
) и постоянстве u(t) º
U дает оптимальное значение U = 0.5 (при a = b = d = 0);  (при b = d = 0).
(при b = d = 0).
Условие v(t) º 0 означает распределение затрат энергии между воспроизводством и репарацией. В этом случае гамильтониан выглядит следующим образом
![]() где
где

Для нахождения оптимальной стратегии необходимо решить четыре дифференциальных уравнения, что можно сделать только численными методами. Другой путь – дискретизация задачи и применение динамического программирования, последнее позволяет построить графики зависимости u от t и q, q от t для разных наборов параметров a, b, c.
Важным результатом решения этой частной задачи является получение увеличения скорости смертности с возрастом. Данная зависимость хорошо согласуется (по крайней мере качественно) с реальными наблюдениями. Обычно ускоренный рост интенсивности смертности с возрастом описывается уравнением Гомпертца-Макехама ![]() (α, β, γ – неотрицательные константы; t – возраст) или уравнением Вейбулла (показательный рост). Получение же такой зависимости из вариационной задачи позволяет объяснить ее требованием эволюционной оптимальности, а именно, необходимостью увеличения с возрастом трат энергии на размножение за счет уменьшения трат на репарацию [47, 21].
(α, β, γ – неотрицательные константы; t – возраст) или уравнением Вейбулла (показательный рост). Получение же такой зависимости из вариационной задачи позволяет объяснить ее требованием эволюционной оптимальности, а именно, необходимостью увеличения с возрастом трат энергии на размножение за счет уменьшения трат на репарацию [47, 21].
Задача о распределении энергии между выживанием и репарацией также решается с помощью динамического программирования.
Принцип максимальной биомассы потомства. Другой аспект изучения распределения организмом энергетических затрат на рост и размножение заключается в попытке объяснить общую закономерность развития многих животных и растений, которая состоит в том, что размножение начинается тогда, когда рост в основном закончен [3]. Предлагается следующий экстремальный принцип: в онтогенезе комбинация между тратами на рост и размножение оптимальная в отношении естественного отбора организмов такова, что биомасса потомства одной особи за все время ее жизни достигает максимума. Для формализации этого принципа вводят обозначения: M(t) – масса ассимиляционного аппарата организма в зависимости от времени t (0 £ t £ T); j (t) – доля M(t), идущая на рост самого организма, 0 £ j (t) £ 1; y (t) – средняя вероятность того, что организм доживет до момента времени t, y (0) = 1, y (Т) = 0.
Предполагается, что за время жизни организм не расходует все свои ресурсы только на рост (![]() ), и все, что не тратится на рост, идет на размножение (1 – j
(t) – доля M(t), расходуемая на размножение). Функция ¦
(t) считается известной и является коэффициентом пропорциональности между приростом M(t) в константной среде и j
(t)×
M(t) (dM(t) = ¦
(t)×
j
(t)×
M(t)dt).
), и все, что не тратится на рост, идет на размножение (1 – j
(t) – доля M(t), расходуемая на размножение). Функция ¦
(t) считается известной и является коэффициентом пропорциональности между приростом M(t) в константной среде и j
(t)×
M(t) (dM(t) = ¦
(t)×
j
(t)×
M(t)dt).
Учитывая принятые обозначения, можно записать выражение для массы ассимилятов, потраченной средним организмом на размножение
 .
.
Итак, задача состоит в следующем: найти такую функцию j
0(t), что ![]() , причем множество {j
} – множество кусочно-непрерывных функций j
(t) – таких, что 0 £
j
(t) £
1 для всех t. Предположение о том, что организм, “управляемый” функцией j
0(t), обладает максимальной биомассой потомства делается на основе тесной связи величины F(j
) и биомассы потомства.
, причем множество {j
} – множество кусочно-непрерывных функций j
(t) – таких, что 0 £
j
(t) £
1 для всех t. Предположение о том, что организм, “управляемый” функцией j
0(t), обладает максимальной биомассой потомства делается на основе тесной связи величины F(j
) и биомассы потомства.
Решение j 0(t) является ступенчатой функцией, принимающей значения 0 и 1, причем, если j 0(t) = 0 при 0 £ t £ b1 (b1 – первая точка переключения функции j 0(t)), то такая функция j 0(t) есть “постороннее” решение, которому не соответствует никакой организм (иначе первое накопление биомассы наступило бы после размножения). Биологический смысл указанного решения заключается в том, что в каждый момент времени организм тратит все ресурсы либо на рост, либо на размножение.
По мнению авторов модели, наиболее адекватно с помощью принципа оптимальности может быть описан рост и размножение некоторых растений, в частности однолетних деревьев, некоторых ракообразных и теплокровных животных, а различные несоответствия в описании развития организмов могут быть объяснены неучтенностью влияния изменения внешней среды, инерцией роста и другими причинами.
Основной результат заключается в том, что тенденция резкого разделения во времени роста и размножения выведена из принципа оптимальности.
ПРИНЦИП ВЫЖИВАНИЯ
В качестве критерия оптимальности предлагается использовать принцип выживания, полагая, что в диаде выживание – приспособленность первичным является выживание [22].
Пусть динамику экосистемы, в которую входит рассматриваемый вид, адекватно описывает система уравнений с неизвестными численностями особей всех элементов экосистемы. В качестве параметров уравнений выступают экологические условия, а также структурно-функциональные параметры особей всех элементов экосистемы. Выделяют s-я популяция и некоторый структурный или функциональный параметр ![]() этой популяции. Делают предположение о том, что популяция состоит из двух подпопуляций, различающихся величиной фенотипического параметра. Пусть xs(1), xs(2),
этой популяции. Делают предположение о том, что популяция состоит из двух подпопуляций, различающихся величиной фенотипического параметра. Пусть xs(1), xs(2), ![]() ,
,![]() – численности и величины фенотипического параметра двух подпопуляций.
– численности и величины фенотипического параметра двух подпопуляций.
Исследование динамической системы, в которую внесены соответствующие изменения, учитывающие различия фенотипического параметра у особей s-ой популяции, позволяет анализировать асимптотические свойства численностей подпопуляций. Один из возможных вариантов поведения – вытеснение второй подпопуляции первой (фенотипический параметр ![]() имеет селективное преимущество по сравнению с параметром
имеет селективное преимущество по сравнению с параметром ![]() в заданных экологических условиях). Математически этот вариант описывается выражениями
в заданных экологических условиях). Математически этот вариант описывается выражениями
![]()
Оптимальной с точки зрения выживания величиной фенотипического параметра ![]() является такая величина, при которой для любого отличного от этого значения параметра
является такая величина, при которой для любого отличного от этого значения параметра ![]() выполняются условия
выполняются условия
![]()
Причем они верны при произвольных начальных условиях. С оптимальной величиной, удовлетворяющей критерию, следует сопоставлять среднее значение фенотипического параметра.
Необходимо отметить, что если популяция не обладает оптимальным значением параметра, то это не значит, что она элиминируется из биоценоза. Однородная популяция может стабильно существовать при любом значении структурно-функционального параметра ![]() , относящимся к области, соответствующей условию стабильного существования популяции, в частности и при значении, не равном оптимальному
, относящимся к области, соответствующей условию стабильного существования популяции, в частности и при значении, не равном оптимальному![]() . Оптимальное же значение устанавливается в результате конкуренции особей с различными значениями рассматриваемого структурно-фенотипического параметра. Именно вследствие этой конкуренции особи с неоптимальными значениями параметра
. Оптимальное же значение устанавливается в результате конкуренции особей с различными значениями рассматриваемого структурно-фенотипического параметра. Именно вследствие этой конкуренции особи с неоптимальными значениями параметра ![]() элиминируются [23].
элиминируются [23].
Применение общего критерия оптимальности возможно путем численного интегрирования уравнений динамики экосистемы при различных величинах рассматриваемого фенотипического параметра. Также возможно применение частных критериев оптимальности, справедливых в конкретных случаях и следующих из общего критерия. Используя критерий отбора, необходимо учитывать ограничения, вытекающие из физико-химических или биологических закономерностей процесса.
В ряде исследований в качестве критерия оптимальности выступало требование максимума относительной скорости роста численности популяции:
![]()
Этот критерий может быть применен для определения оптимальных величин структурно-функциональных параметров, если относительная скорость роста численности представлена в виде функции этих параметров. Причем, если рассматриваемый параметр не зависит от возраста особи, то задача нахождения оптимального значения сводится к отысканию параметра, соответствующего максимуму относительной скорости роста; если же рассматриваемый параметр зависит от возраста, то искомая оптимальная зависимость может быть определена путем решения соответствующей вариационной задачи [23].
Общий критерий оптимальности применяли к исследованию популяций лосей в лесном биоценозе. Оптимизируемыми параметрами были начальный вес новорожденных и рождаемость. Кроме того, из общего критерия оптимальности выводили требование максимума относительной скорости роста популяции, а затем на основании этого требования оптимизировали функцию роста, определяющая зависимость веса тела особи от возраста. Сравнение теоретических величин, полученных для лосей, и соответствующих биологических данных свидетельствовали об их хорошем согласии.
В теории оптимальных биологических процессов применимы более простые критерии, например, определяющие оптимальность структурно-функциональных параметров органов и систем, роль которых в организме сводится к выполнению определенных функций. Критерием оптимальности такого органа является условие минимума его потребностей при условии выполнения этим органом заданных функций
![]() (4)
(4)
где Пор – потребности органа; Пп – потребление пищи в единицу времени, связанное с поддержанием жизненного органа, не несущего функциональную нагрузку; Пf – потребление пищи в единицу времени, связанное с осуществлением органом его функций в организме. Использование критерия (4) требует учитывать условия, определяющие функции, выполняемые органом или системой.
Критерий, определяющий оптимальные функциональные параметры, имеет вид: Пf = min. Здесь необходимо сформулировать дополнительные условия, определяющие функции органа.
Если определяющей является энергетическая деятельность органа, то критерий оптимальности может быть сформулирован в виде ![]() , где Wi – мощность, потребляемая i-м органом.
, где Wi – мощность, потребляемая i-м органом.
Авторами цитируемой работы представлено применение общего критерия отбора для определения оптимального в эволюционном смысле начального веса новорожденных (на примере данных биологических исследований для популяции лосей); энергетического критерия оптимальности (4) для определения функционального состояния системы транспорта кислорода при физической нагрузке и при ее отсутствии, а так же для нахождения энергетически оптимальной концентрации эритроцитов в крови, парциального давления в артериальной и венозной крови, определения оптимальных функциональных параметров системы внешнего дыхания и др.
ПРИНЦИП МАКСИМИЗАЦИИ РЕПРОДУКТИВНЫХ УСИЛИЙ
В качестве общего критерия экологического моделирования предлагается использовать максимизирование репродуктивных усилий [56]. Рост растительности и все другие процессы должны быть представлены в модели как путь к максимизации усилий направленных на воспроизводство. Вместо простого описания роста или смерти, любой процесс, происходящий в лесу, должен рассматриваться как вклад в конечную цель жизни дерева. Акцентирование внимания на максимизации репродуктивных усилий не обязательно усложняет модель, поскольку для их определения не требуется подсчета каждого семени. Затраты на воспроизведение потомства эквивалентны разнице между усилиями, затраченными на рост и отдачей в форме ассимиляции. Параметры модели подбираются так, чтобы максимизировать эту разницу.
Результат такого подхода часто оказывается неожиданным. Так, например, рост обычно изображается гладкой кривой, дифференцируемой в каждой точке. Эта гладкость скрывает излом, являющийся индикатором начала репродукции. Как было доказано математически, в предсказуемой среде максимум репродуктивных усилий достигается только с полным переключением от вегетативного роста к производству семян. Недостаточная предсказуемость среды сглаживает переход.
Когда рост рассматривается как путь к максимизации репродуктивных усилий, кривая роста может обеспечить гораздо больше информации, в частности, она может обнаружить интенсивность конкуренции, ответственной за время переключения, ожидаемое время жизни и степень предсказуемости среды.
ПРИНЦИП МАКСИМАЛЬНОЙ НЕОЖИДАННОСТИ ПРОТЕКАНИЯ ЭВОЛЮЦИИ
Один из путей исследования динамики популяций – изучение “дарвиновских систем”, описывающих динамику естественного отбора в биологических популяциях. Одним из исследователей этих объектов является Е.В.Евдокимов, в работе которого приведено определение и способ описания дарвиновских систем по М.Эйгену [1]. Дарвиновские системы (ДС) являются открытыми системами, состоящими из самокопирующихся с небольшим количеством ошибок единиц различных видов, использующих для своего размножения вещество и свободную энергию поступающих извне питательных компонентов. Обязательными ограничениями являются либо постоянство суммарной организации системы, либо постоянство потоков. Для описания ДС используют дифференциальное уравнение
![]() , (5)
, (5)
которое можно свести к достаточно простому виду
![]() (6)
(6)
где i, j=1,...,w (w = const) – число квазивидов в системе, s = (s1,..., sm) – концентрации питательных компонентов, ![]() – удельная скорость размножения i-го квазивида, D – скорость протока в системе. В зависимости от наложенных ограничений различают ДС с постоянной организацией (ДСПО) – у которых сумма
– удельная скорость размножения i-го квазивида, D – скорость протока в системе. В зависимости от наложенных ограничений различают ДС с постоянной организацией (ДСПО) – у которых сумма ![]() и концентрация s постоянны, и ДС с постоянным протоком (ДСПП), характеризующиеся условием D = const.
и концентрация s постоянны, и ДС с постоянным протоком (ДСПП), характеризующиеся условием D = const.
Изучению ДС посвящено много работ, однако, при экспериментальных исследованиях возникает проблема неполноты их описания с помощью систем (5 и 6) из-за практической труднодоступности информации на микроуровне [1]. Для избежания подобных трудностей была предпринята попытка использовать формализм Джейнса. В своей работе Е.В.Евдокимов предложил модификацию этого метода: “В соответствии с общим подходом потребуем, чтобы процесс эволюции ДС протекал наименее неожиданным способом” (принцип минимальной неожиданности протекания эволюции). В качестве целевой функции используется функция неожиданности эволюции ДСПО
![]()
где ![]() – вероятность того, что случайно выбранная в момент t особь имеет мальтузианский параметр
– вероятность того, что случайно выбранная в момент t особь имеет мальтузианский параметр ![]()
![]() , значения yk0 – задаются экспериментально.
, значения yk0 – задаются экспериментально.
Итак, вариационная задача формулируется следующим образом
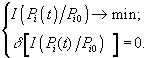
Решение было получено методом неопределенных множителей Лагранжа

причем оно соответствует решению системы уравнений (6).
Важное значение имеет множитель Лагранжа ![]() , поскольку, придавая ему информационный смысл, можно получить “основную теорему естественного отбора” Фишера
, поскольку, придавая ему информационный смысл, можно получить “основную теорему естественного отбора” Фишера
![]()
Другое важное следствие состоит в том, что множитель λ0 с точностью до коэффициента пропорциональности равен среднему по популяции числу поколений.
При рассмотрении энергетических трат на эволюцию было получено, что множитель λ0 пропорционален энергопотреблению популяции.
Таким образом, исходя из эвристического принципа минимальной неожиданности протекания эволюционного процесса, Е.В.Евдокимов получил результаты, “описывающие динамику отбора в дарвиновских системах, которые полностью идентичны уравнениям, выводимым из кинетики размножения и конкуренции саморедуплицируемых единиц на микроуровне”, а множители Лагранжа, использующиеся для решения вариационной задачи, имеют биологический смысл и прогностическую ценность.
ЛОГИСТИЧЕСКОЕ УРАВНЕНИЕ КАК ЭКСТРЕМАЛЬ ФУНКЦИОНАЛА ДЕЙСТВИЯ
Один из способов применения целевой функции состоит в формулировании общего утверждения относительно поведения системы. Хорошо известные экстремальные принципы относятся к этому случаю. Самый известный из них – принцип Гамильтона, согласно которому, каждая механическая система ведет себя так, чтобы действие (интеграл по времени от функции Лагранжа) было минимальным. В экологии предпринимались попытки использования этого подхода для получения уравнения роста популяции, точнее, рассматривалась обратная задача: записать действие, которое приведет к специальному уравнению роста. Одна из наиболее удачных попыток разрешить эту задачу, предложенная М.Гатто с соавторами [28, 29], представлена в работе Дж.Вебба [52].
В качестве функционала действия, который приведет к логистическому уравнению роста популяции численности n, было рассмотрено следующее выражение
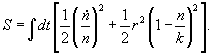
Для упрощения вычисления была сделана замена переменных
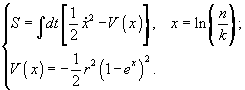 (7)
(7)
Согласно вариационному принципу, уравнение эволюции x(t) задается требованием экстремальности действия, т.е. dS = 0. После необходимых вычислений было получено динамическое уравнение
![]()
![]() (8)
(8)
Чтобы сравнить этот результат с логистическим уравнением ![]() его переписали в переменных
его переписали в переменных ![]() и продифференцировали:
и продифференцировали: ![]() Полученное совпадение показывает, что любое решение логистического уравнения является решением динамического уравнения, выведенного из функционала действия. Однако, не любое решение уравнения (8) является решением логистического уравнения. Для выявления взаимосвязи между данными уравнениями было проведено исследование полученного уравнения эволюции. После некоторых преобразований и интегрирования было получено выражение
Полученное совпадение показывает, что любое решение логистического уравнения является решением динамического уравнения, выведенного из функционала действия. Однако, не любое решение уравнения (8) является решением логистического уравнения. Для выявления взаимосвязи между данными уравнениями было проведено исследование полученного уравнения эволюции. После некоторых преобразований и интегрирования было получено выражение
![]()
Уравнение эволюции характеризуется константой R: при R > 0 популяция неограниченно растет, при R < 0 популяция достигает максимального значения, а затем уменьшается до 0. Значение R = 0 приводит к логистическому уравнению, тем самым, показывая, что логистический рост – это особый случай равновесия между неограниченным ростом и затуханием.
В работе также был рассмотрен вопрос об интерпретации введенного таким образом “биологического” действия. Описание в терминах кинетической и потенциальной энергии неприемлемо, поскольку ведет к неизменности общей энергии системы (экологические системы обычно подразумеваются открытыми). По аналогии с физикой, где действие разделено на свободное движение и взаимодействие, предлагалось рассматривать действие (7) как сумму члена, описывающего популяцию, которая не подвержена помехам в росте, и члена V(x), описывающего внешнее влияние среды на популяцию. Однако, подобная интерпретация хорошо описывает лишь случай V(x) = 0, когда применение вариационного принципа приводит к уравнению экспоненциального роста. Сам М.Гатто и его соавторы описывали действие как цену роста.
По мнению Дж.Вебба, применение вариационного принципа позволяет сместить акцент с поведения системы на факторы, которые его определяют, а также делает возможным разделение внутреннего поведения популяции и эффектов внешней среды.
ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ И ПРИНЦИП МАКСИМУМА ПОНТРЯГИНА В БИОЭКОНОМИЧЕСКОЙ МОДЕЛИ
Рассматривается простая модель вылова двух конкурирующих видов рыб, подчиняющихся закону логистического роста [27]. Система уравнений, описывающая данную ситуацию, записывается следующим образом
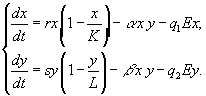
Здесь r, s представляют собой экологический потенциал, K, L – пропускные способности двух видов, члены ![]() и
и ![]() отражают борьбу за общий ресурс, q1 и q2 – коэффициенты вылова видов и E – усилия, затраченные на их совместный вылов. Предполагается, что существует внешний ресурс, поддерживающий каждый вид.
отражают борьбу за общий ресурс, q1 и q2 – коэффициенты вылова видов и E – усилия, затраченные на их совместный вылов. Предполагается, что существует внешний ресурс, поддерживающий каждый вид.
В работе исследуют состояния экологического равновесия, динамику поведения, а также оптимальную стратегию вылова. Чистый доход в любой момент времени определяется формулой: ![]() где С – цена рыбной ловли, пропорциональная усилиям. Предлагается максимизировать общий дисконтированный доход для
где С – цена рыбной ловли, пропорциональная усилиям. Предлагается максимизировать общий дисконтированный доход для ![]() :
: ![]() , δ – мгновенная годовая скорость дисконтирования. Применяя принцип максимума Понтрягина, максимизируется функционал:
, δ – мгновенная годовая скорость дисконтирования. Применяя принцип максимума Понтрягина, максимизируется функционал: ![]() . Были найдены оптимальные равновесные величины популяций, которые ведут к ситуации, когда общая цена улова на единицу усилий равна дисконтированной величине будущей цены. Согласно полученным результатам, при бесконечно большом значении мгновенной годовой скорости дисконтирования δ рыбный промысел должен быть закрыт ввиду полного рассеяния приносимого им дохода, а значение δ = 0 ведет к максимуму дохода, непрерывно получаемого от вылова. Однако, существование такой биоэкономической стабильности зависит от трофической интенсивности обоих видов и неизбежно влечет за собой самоограничение видов.
. Были найдены оптимальные равновесные величины популяций, которые ведут к ситуации, когда общая цена улова на единицу усилий равна дисконтированной величине будущей цены. Согласно полученным результатам, при бесконечно большом значении мгновенной годовой скорости дисконтирования δ рыбный промысел должен быть закрыт ввиду полного рассеяния приносимого им дохода, а значение δ = 0 ведет к максимуму дохода, непрерывно получаемого от вылова. Однако, существование такой биоэкономической стабильности зависит от трофической интенсивности обоих видов и неизбежно влечет за собой самоограничение видов.
МАКСИМИЗАЦИЯ ФУНКЦИИ ЭНТРОПИИ
Эффективное применение вариационных принципов в статистической физике и в теории информации в виде условной максимизации функции энтропии для характеристики стационарного состояния сложной системы дало толчок к использованию подобного инструмента для решения некоторых биологических проблем. В частности, А.К.Приц рассматривает популяцию как открытую термодинамическую систему, стремящуюся сохранить свою структуру, описываемую функцией энтропии, неизменной во времени [17]. В работах Д.Лурье с соавторами [36] предлагается условная максимизация энтропиеподобной функции для описания адаптивного поведения сложной системы. А.П.Левичем и его коллегами моделируется сообщество одноклеточных организмов с применением вариационной задачи на условный экстремум обобщенной энтропии [4, 13, 33].
Принцип стационарного состояния открытых систем. А.К.Приц [17], изучая возрастную структуру популяции рыб, видел большое значение подобных исследований для рыболовного промысла (предсказание будущих уловов и предотвращение переуловов).
В качестве статистической характеристики состояния популяции, по которой можно судить об изменениях возрастной структуры, А.К.Приц предложил энтропию S: ![]() , где
, где ![]() Эти обозначения соответствуют численности популяции (N), числу особей возраста i лет (Ni), предельному возрасту особей популяции (n). Вклад каждой возрастной группы в общую численность представляет собой вероятность pi встретить особь возраста i лет среди N особей популяции.
Эти обозначения соответствуют численности популяции (N), числу особей возраста i лет (Ni), предельному возрасту особей популяции (n). Вклад каждой возрастной группы в общую численность представляет собой вероятность pi встретить особь возраста i лет среди N особей популяции.
Популяция рассматривается как “открытая термодинамическая система, находящаяся в состоянии непрерывного обмена с окружающей средой, самовоспроизводящаяся и саморегулирующаяся”. А.К.Приц предлагает исходить из принципа стационарного состояния открытых систем, согласно которому все живые системы стремятся сохранить свою структуру (и энтропию) неизменной во времени.
Энтропия популяции записывается в виде ![]() общая фиксированная численность задается выражением
общая фиксированная численность задается выражением ![]() , а фиксированная масса популяции – выражением
, а фиксированная масса популяции – выражением ![]() (mi – масса одной особи i-го возраста).
(mi – масса одной особи i-го возраста).
Задача нахождения условий, при которых осуществляется стационарное состояние, удовлетворяющее перечисленным выше условиям, решается применением метода неопределенных множителей Лагранжа к системе
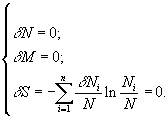
В результате была получена формула, определяющая связь между возрастной численностью i-й группы Ni, массой mi отдельной особи i-го возраста и общей численностью популяции N
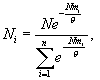 (9)
(9)
где θ – модуль статистического распределения различных особей по возрастам, который определяется из эксперимента на основе физических соображений.
Формула (9) может быть представлена в несколько ином виде, если в качестве фиксированного параметра взять среднее время жизни популяции Т, ![]() (ti – возраст i-й группы популяции)
(ti – возраст i-й группы популяции)
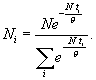 (10)
(10)
Для практического применения формулы (10) интересным представляется вид параметра θ. А.К.Приц получил соотношение θ = Nm1, справедливое для долгоживущих рыб. Такой вид параметра θ обеспечивает оптимальности пополнения популяции, т.е. численности N1 (в условиях интенсивного вылова воспроизводство должно быть максимальным). При выводе указанного соотношения предполагалось, что система находится в стационарном состоянии. Формула (9) может быть теперь записана как 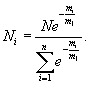 Зная по результатам экспериментального лова массу mi особи i-го возраста, а также число особей Ni, можно найти общую численность популяции N и остальные численности Nj, общую массу популяции. Были проведены расчеты для сельди Северного моря с 1947 по 1971 год. Сравнение расчетных и реальных значений дало совпадение от 70% и выше за каждый год, кроме одного.
Зная по результатам экспериментального лова массу mi особи i-го возраста, а также число особей Ni, можно найти общую численность популяции N и остальные численности Nj, общую массу популяции. Были проведены расчеты для сельди Северного моря с 1947 по 1971 год. Сравнение расчетных и реальных значений дало совпадение от 70% и выше за каждый год, кроме одного.
Предсказание численностей различных возрастных групп дает возможность рассчитывать ежегодный прирост биомассы по всей популяции
![]()
что, в свою очередь, позволяет регулировать промысел для поддержания стабильного значения биомассы. Причем найденный прирост ∆М и определяет максимально возможный вылов в соответствии со стратегией оптимального вылова.
Принцип максимального разнообразия. По мнению Д.Лурье и его коллег [36] живым системам присуще адаптивное поведение, которое обусловлено конкуренцией между двумя тенденциями – тенденцией к большему разнообразию, происходящей из постоянного появления ошибок в генетическом коде, и тенденцией к меньшему разнообразию из-за естественного отбора. Для математического выражения этой конкуренции предлагается ввести понятие удельного разнообразия биомассы ![]() , которое находится в тесной связи с физическими параметрами экосистемы
, которое находится в тесной связи с физическими параметрами экосистемы
![]()
где p(m) – плотность вероятности распределения биомассы. В качестве задачи ставится нахождение функции плотности распределения биомассы, максимизирующей разнообразие ω при ограничении на полную биомассу M, которую может поддерживать эта система ![]() где N – количество особей данной системы,
где N – количество особей данной системы, ![]() – средняя биомасса особи.
– средняя биомасса особи.
Итак, рассматривается вариационная задача
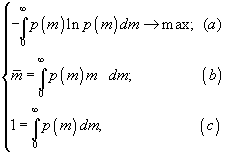
здесь в (а) для удобства используется натуральный логарифм, (b) представляет собой запись ограничения в терминах средней биомассы, (с) – условие нормировки распределения p(m).
Решение задачи методом неопределенных множителей Лагранжа дает следующую экспоненциально убывающую функцию биомассы
![]()
Также было предложено дискретное рассмотрение проблемы. Область значений биомассы разделяется на r интервалов размером ![]() . В этом случае разнообразие биомассы определяется выражением
. В этом случае разнообразие биомассы определяется выражением
![]()
где ni – число особей экосистемы в i-м интервале, независимо от вида, ![]() (для больших популяций
(для больших популяций ![]() ).
).
Введя обозначение ![]() и записав в дискретной форме ограничение и условие нормировки, получим систему
и записав в дискретной форме ограничение и условие нормировки, получим систему
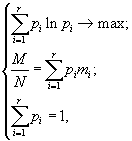
где mi – представительное значение биомассы особей из i-го интервала.
Решение данной вариационной задачи задается формулой: 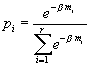 . Для нахождения множителя Лагранжа β и знаменателя дроби в выражении для относительной численности pi необходим переход к пределу и интегрирование (
. Для нахождения множителя Лагранжа β и знаменателя дроби в выражении для относительной численности pi необходим переход к пределу и интегрирование (![]() ,
,![]() ). Проделав необходимые операции, получим уже выведенную ранее формулу
). Проделав необходимые операции, получим уже выведенную ранее формулу ![]()
Описанные теоретические результаты были проверены на различных данных о распределениях рыб по весам в уловах. Коэффициент корреляции изменялся от 0,986 до 0,998. Рассмотрение дискретной записи задачи предполагает зависимость разнообразия ω от разбиения биомассы экосистемы на классы ![]() . Для данных одной из экспедиций были проведены расчеты с различными
. Для данных одной из экспедиций были проведены расчеты с различными ![]() , при этом были получены значения коэффициентов корреляции 0,971; 0,979; 0,986.
, при этом были получены значения коэффициентов корреляции 0,971; 0,979; 0,986.
Следует отметить недостаток предложенной теории, на который обратил внимание Дж.Розен [44] в своей работе “Замечание по поводу разнообразия биомассы в экологии”: “…в постулате Лурье-Вагенсберга все ячейки биомассы размера ![]() a priori обладают одинаковым статистическим весом, хотя такое предположение об эквивалентности
a priori обладают одинаковым статистическим весом, хотя такое предположение об эквивалентности ![]() -ячеек противоречит соображениям эргодичности, основанным на динамике популяции”.
-ячеек противоречит соображениям эргодичности, основанным на динамике популяции”.
В качестве альтернативы Дж.Розеном был предложен динамический подход. Рассматривается уравнение динамической непрерывности для распределения биомассы в большой популяции рыб:
![]()
Здесь m – биомасса индивидуума, n = n(t,m) – число индивидуумов на единичный интервал биомассы, ![]() – положительная средняя скорость накопления биомассы,
– положительная средняя скорость накопления биомассы, ![]() – положительная средняя дисперсионная скорость для n, обусловленная генетическими различиями и различиями в условиях окружающей среды, а
– положительная средняя дисперсионная скорость для n, обусловленная генетическими различиями и различиями в условиях окружающей среды, а ![]() – положительная средняя удельная скорость, с которой индивидуумы удаляются из популяции. Величины
– положительная средняя удельная скорость, с которой индивидуумы удаляются из популяции. Величины ![]() аппроксимируются усредненными по времени и массе постоянными. Общее решение динамического уравнения с учетом указанных ограничений приводит к асимптотическому стационарному уравнению:
аппроксимируются усредненными по времени и массе постоянными. Общее решение динамического уравнения с учетом указанных ограничений приводит к асимптотическому стационарному уравнению: ![]() , где численность n удовлетворяет уравнению
, где численность n удовлетворяет уравнению
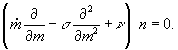 (11)
(11)
Решение уравнения (11) задается формулой ![]() где А – свободная константа, зависящая от начального значения численности n = n(t,m), а значение
где А – свободная константа, зависящая от начального значения численности n = n(t,m), а значение ![]() определяется уравнением
определяется уравнением  .
.
Вернемся к теории Лурье-Вагенсберга. Как уже отмечалось выше, результаты, полученные по выведенным формулам, хорошо согласуются с некоторыми опытными данными. Однако, это касается только тех популяций, в которых нет прямого взаимодействия между различными классами биомассы, что соответствует использованию в теоретическом выводе независимости вероятностей pi. В частности, гипотеза оказалась полностью несостоятельной при описании популяций хека, который характеризуется каннибалистическим поведением. В работе Дж.Вагенсберга и Дж.Валлса [50] была предложена модификация принципа максимума энтропии, описывающая внутреннее взаимодействие популяции “хищник-жертва”.
Популяция предполагается состоящей из двух взаимодействующих классов, каждый из которых внутренне независим. Пусть ![]() – вероятность нахождения хищника в j-м классе биомассы, p(mi) – вероятность нахождения жертвы в i-м классе биомассы,
– вероятность нахождения хищника в j-м классе биомассы, p(mi) – вероятность нахождения жертвы в i-м классе биомассы,  – условная вероятность, связанная соотношением
– условная вероятность, связанная соотношением 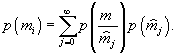 Энтропия теперь выглядит следующим образом
Энтропия теперь выглядит следующим образом
![]() , где
, где 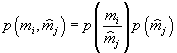 . (12)
. (12)
Предлагаются следующие гипотезы:
1) внутренне взаимодействие определенной популяции характеризуется определенной матрицей взаимодействия, для элементов которой выполнено
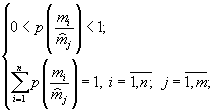
2) устойчивая статистическая структура для данной матрицы взаимодействия ![]() максимизирует объединенную энтропию хищника и жертвы при ограничениях
максимизирует объединенную энтропию хищника и жертвы при ограничениях
 (13)
(13)
При решении методом неопределенных множителей Лагранжа вариационной задачи, составленной из уравнений (12, 13) (![]() ) было получено распределение биомассы
) было получено распределение биомассы
![]() . (14)
. (14)
Значение нормировочного множителя Z и множителя Лагранжа β вычисляются при подстановке выражения (14) в условия (13). Структура “жертвы” вычисляется с помощью формулы для величины p(m).
Для проверки модифицированной гипотезы была рассмотрена популяция хека, состоящая из особей возраста от одного года до 13 лет. Соответственно было выделено 13 классов массы. Особи первых 7-ми классов предполагались жертвами, остальные, с 8-го по 13-й – хищниками, т.е. уравнение для p(m) имело вид

(все массы ![]() и матрица
и матрица ![]() – известны).
– известны).
Сравнение вычисленных и наблюдаемых распределений показало, что различие в коэффициенте β составляет 0,71% против 70% для гипотезы, не учитывающей эффект каннибализма, а коэффициент корреляции составил 0,999.
Принцип максимума обобщенной энтропии. Применение современных методов вариационного моделирования в экологии сообществ содержится в работах А.П.Левича с коллегами [4, 13, 33]. Моделируется сообщество одноклеточных организмов, потребляющих ресурсы, которые не могут заменить друг друга, поскольку выполняют различные функции по отношению к росту. Допустимо деление клеток, смертность, но не их слияние. В лабораторных условиях описываемая модель соответствует накопительному культивированию, при котором не происходит добавление или изъятие ресурсов и микроорганизмов. Изучается развитие поликультуры до остановки роста, вызванной исчерпанием одного из ресурсов, но не какими-либо иными причинами.
Постулируется, что динамические системы из заданного состояния переходят в состояние с экстремальной (в пределах, допустимых имеющимися ресурсами) структурой. Соответствующая вариационная задача на условный экстремум выглядит следующим образом [13, 33]:
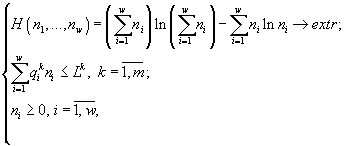 (15)
(15)
где ni – конечная искомая численность каждого из видов, ![]() – количество k-ого ресурса, необходимое для роста вида i, в расчете на одну клетку, называемое потребностью вида i в ресурсе k, m – общее количество взаимонезаменимых ресурсов, потребляемых сообществом, w – число видов в сообществе, Lk – начальное содержание ресурса k в среде (Lk
– количество k-ого ресурса, необходимое для роста вида i, в расчете на одну клетку, называемое потребностью вида i в ресурсе k, m – общее количество взаимонезаменимых ресурсов, потребляемых сообществом, w – число видов в сообществе, Lk – начальное содержание ресурса k в среде (Lk ![]() ) Отметим, что условия, ограничивающие экстремум, имеют форму неравенств, а не равенств.
) Отметим, что условия, ограничивающие экстремум, имеют форму неравенств, а не равенств.
![]() Важно также отметить, что функционал
Важно также отметить, что функционал ![]() , названный обобщенной энтропией, не постулируется, а выводится [5] на основе категорно-функторного метода сравнения математических структур.
, названный обобщенной энтропией, не постулируется, а выводится [5] на основе категорно-функторного метода сравнения математических структур.
Основным результатом, на котором базируется последующее исследование сформулированной задачи, является теорема стратификации. Приводим ее формулировку. Все пространство ресурсных факторов ![]() распадается (стратифицируется) на
распадается (стратифицируется) на ![]() непересекающихся областей (стратов), каждая из которых соответствует одному из подмножеств множества потребляемых сообществом ресурсов. В страте SJ, где J — непустое подмножество множества ресурсов {1,2,...,m}, выполняется:
непересекающихся областей (стратов), каждая из которых соответствует одному из подмножеств множества потребляемых сообществом ресурсов. В страте SJ, где J — непустое подмножество множества ресурсов {1,2,...,m}, выполняется:
1) решение задачи (15) ![]() , где
, где ![]() º
{L1, L2,..., Lm}, зависят только от тех Lk, для которых kÎ
J;
º
{L1, L2,..., Lm}, зависят только от тех Lk, для которых kÎ
J;
2) на этом решении нестрогие неравенства ![]() обращаются в строгие равенства для всех kÎ
J и в строгие неравенства для всех kÏ
J;
обращаются в строгие равенства для всех kÎ
J и в строгие неравенства для всех kÏ
J;
Теорема стратификации влечёт редукцию задачи (15) к задачам
 (16)
(16)
формулируемым для любого J Ì {1,2,...,m} [8].
Биологическая интерпретация теоремы стратификации задаёт правило лимитирующего звена для многовидовых сообществ, популяции из которых конкурируют за несколько ресурсов [12]. Лимитирующими называются ресурсы, потребляемые сообществом из среды полностью, т.е. те, для которых балансовые неравенства задачи (15) превращаются в равенства. Согласно теореме стратификации, из заданной совокупности ресурсов ![]() полностью потребляются, т.е. лимитируют рост сообщества, ресурсы из набора J, идентифицирующего страт SJ, которому принадлежит заданный вектор
полностью потребляются, т.е. лимитируют рост сообщества, ресурсы из набора J, идентифицирующего страт SJ, которому принадлежит заданный вектор ![]() . Таким образом, теорема стратификации позволяет строго предсказывать ресурсы, лимитирующие рост сообщества с заданным набором потребностей
. Таким образом, теорема стратификации позволяет строго предсказывать ресурсы, лимитирующие рост сообщества с заданным набором потребностей ![]() . Результаты подробного изучения некоторых конкретных примеров одно-, двух и трехфакторного лимитирования представлены в книге А.П.Левича с соавторами [13].
. Результаты подробного изучения некоторых конкретных примеров одно-, двух и трехфакторного лимитирования представлены в книге А.П.Левича с соавторами [13].
Решение задач (16) получило название формулы видовой структуры [4]
![]()
где вектора ![]() ,
, ![]() и
и ![]() имеют компоненты j из набора J, идентифицирующего страт, которому принадлежит вектор
имеют компоненты j из набора J, идентифицирующего страт, которому принадлежит вектор ![]() . Множители Лагранжа
. Множители Лагранжа ![]() и полная численность n как функции потребляемых полностью в страте SJ ресурсов
и полная численность n как функции потребляемых полностью в страте SJ ресурсов ![]() ищутся из алгебраических уравнений
ищутся из алгебраических уравнений
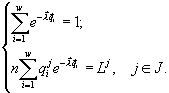
Для проверки адекватности модели был проведен ряд экспериментов [13] с поликультурой из 10-ти видов зелёных микроводорослей (Chlorella vulgaris (Bejerink.), Scotiella nivalis (Fritsch.), Chromochloris cinnoborina (Chodat.), S. quadricauda (Turp.), Scenedesmus bijugatus (Lagerh.), Scenedesmus obliquus (Kruger.), Ankistrodesmus acicularis (Korschik.), A. braunii (Brunnth.), Stichococcus mirabilis (Lagerh.) и Chlamydomonas humicola (Luksch.)) Сравнение численностей видов, рассчитанных по формуле видовой структуры, и экспериментальных данных показало, что предсказанные моделью значения видовых обилий совпадают с измеренными в опыте в пределах экспериментальных ошибок (см. также описание других экспериментов с лабораторными альгоценозами в [13]).
Важным свойством формулы видовой структуры является зависимость относительных численностей только от отношений ресурсов, что позволяет управлять видовыми обилиями с помощью отношений ресурсов в среде. Доказано [9, 24], что относительная численность некоторого вида принимает наибольшее возможное значение при отношениях ресурсов в среде, равных отношениям потребностей в этих ресурсах у данного вида. Эта гипотеза была испытана в традиционной имитационной модели процессов потребления и роста для фитопланктона [7]. Законы Моно, Друпа и сохранения вещества, использованные в модели, являются эмпирическими обобщениями. Тем самым вся модель работает как "большая аппроксимирующая формула", аккумулирующая опытные знания. Машинные эксперименты с моделью показали, что в этих накопленных десятилетиями знаниях неявно заложены эффекты зависимости относительных обилий популяций сообщества от исходных отношений количеств ресурсов в среде. При этом оптимальные для каждого вида отношения оказались близки к отношениям минимальных клеточных квот для этого вида. Другими словами, формальная теорема вариационного моделирования была подтверждена современными представлениями о функционировании фитопланктонных сообществ, заложенными в традиционную феноменологическую модель.
Кроме того, гипотеза о роли отношений концентраций питательных веществ была проверена в ряде экспериментов по регуляции состава альгоценозов с лабораторными поликультурами и с сообществами естественного фитопланктона in vitro и in situ [14, 10, 11, 13, 6, 34, 26].
ЭКСТРЕМАЛЬНЫЙ ПРИНЦИП В ОПИСАНИИ МИКРОБИОЛОГИЧЕСКИХ ПРОЦЕССОВ
Математическая модель, основанная на вариационных принципах была использована для описания явления диауксии (рост бактерий на смеси субстратов разной доступности), а также для нахождения макроскопического показателя выхода биомассы по стехиометрии индивидуальных метаболических реакций [15]. Рассмотрена следующая схема. Рост микроорганизмов представлен как результат совокупности метаболических реакций, в результате которых экзосубстраты превращаются в клеточные компоненты. Каждый из бесконечного множества внутриклеточных путей имеет свою “цену” в виде расхода лимитирующего вещества на построение единицы биомассы, но существует единственный маршрут с наименьшей ценой. В случае хемостата принято, что цена ![]() стремится к минимуму. При заданных скорости потока D и начальной концентрации субстрата s0 минимальному значению цены соответствует максимальная продуктивность хемостата
стремится к минимуму. При заданных скорости потока D и начальной концентрации субстрата s0 минимальному значению цены соответствует максимальная продуктивность хемостата ![]() (μ – удельная скорость прироста биомассы). В соответствии с предлагающимся экстремальным принципом, клеткой выбирается именно этот маршрут с помощью естественных регуляторных механизмов. В качестве примера рассмотрена модель роста, лимитированного источником азота. Выделено 6 переменных – одна внешняя и пять внутренних: интередиаты L, а также высокомолекулярные соединения, которые синтезируются из интередиатов L – транспортные белки Р1, ферменты небелкового синтеза Р2, рибосомальная РНК R, и прочие каталитически неактивные компоненты биомассы
(μ – удельная скорость прироста биомассы). В соответствии с предлагающимся экстремальным принципом, клеткой выбирается именно этот маршрут с помощью естественных регуляторных механизмов. В качестве примера рассмотрена модель роста, лимитированного источником азота. Выделено 6 переменных – одна внешняя и пять внутренних: интередиаты L, а также высокомолекулярные соединения, которые синтезируются из интередиатов L – транспортные белки Р1, ферменты небелкового синтеза Р2, рибосомальная РНК R, и прочие каталитически неактивные компоненты биомассы ![]() . Пул низкомолекулярных N-соединений L непрерывно восполняется за счет активного транспорта и расходуется на биосинтез четырех макромолекулярных компонентов по разветвленной цепочке. В первой точке ветвления разделение потока интередиатов L осуществляется по соотношению внутреклеточных концентраций рибосомальных РНК R и ферментов Р2. Далее каждый из потоков делится еще раз специальными регуляторными операторами a
(распределение потока L между белками Р1 и ферментами Р2) и b
(распределение потока L между концентрациями рибосомальных РНК R и биомассой
. Пул низкомолекулярных N-соединений L непрерывно восполняется за счет активного транспорта и расходуется на биосинтез четырех макромолекулярных компонентов по разветвленной цепочке. В первой точке ветвления разделение потока интередиатов L осуществляется по соотношению внутреклеточных концентраций рибосомальных РНК R и ферментов Р2. Далее каждый из потоков делится еще раз специальными регуляторными операторами a
(распределение потока L между белками Р1 и ферментами Р2) и b
(распределение потока L между концентрациями рибосомальных РНК R и биомассой ![]() ), a
, b
Î
[0, 1]. Каждой паре операторов a
, b
отвечает один единственный набор установившихся концентраций всех выделенных переменных. Таким образом, операторы a
и b
могут быть использованы как инструменты оптимального управления. Модель описывается системой уравнений
), a
, b
Î
[0, 1]. Каждой паре операторов a
, b
отвечает один единственный набор установившихся концентраций всех выделенных переменных. Таким образом, операторы a
и b
могут быть использованы как инструменты оптимального управления. Модель описывается системой уравнений

Здесь Ks, KL – константы полунасыщения; qs, qL – удельные скорости потребления ресурса; ks, kL – максимальные удельные скорости потребления ресурса; σx, σP – клеточные квоты; параметры s0, Ks, KL, ks, kL, σx, σP – константы.
Для нахождения установившегося состояния в хемостате производные в системе уравнений приравниваются нулю, затем решается получившаяся система алгебраических уравнений. Суть оптимизационной задачи состоит в нахождении таких операторов a
и b
, при которых минимизируется расход субстрата на синтез единицы биомассы ![]() во всей области допустимого варьирования скорости протока D (
во всей области допустимого варьирования скорости протока D (![]() – значение биомассы в установившемся режиме). Эта задача эквивалентна поиску максимума биомассы
– значение биомассы в установившемся режиме). Эта задача эквивалентна поиску максимума биомассы ![]() для заданных значений D и s0.
для заданных значений D и s0.
ПРИНЦИП МАКСИМУМА МАЛЬТУЗИАНСКОГО ПАРАМЕТРА
Пусть сообщество состоит из w популяций. В каждый момент времени оно может быть описано численностями (или биомассами) составляющих его популяций xi. Пусть ![]() – суммарная биомасса сообщества. Пусть каждая популяция характеризуется мальтузианским параметром
– суммарная биомасса сообщества. Пусть каждая популяция характеризуется мальтузианским параметром ![]() из уравнения
из уравнения ![]() . Пусть
. Пусть ![]() – относительное обилие i-го вида в сообществе. Тогда набор p = {p1,…,pw} – называется структурой сообщества; величина
– относительное обилие i-го вида в сообществе. Тогда набор p = {p1,…,pw} – называется структурой сообщества; величина ![]() – средним мальтузианским параметром сообщества (
– средним мальтузианским параметром сообщества (![]() ), а динамика общей биомассы описывается уравнением
), а динамика общей биомассы описывается уравнением ![]()
Постулируется принцип максимума среднего мальтузианского параметра: сообщество взаимодействующих популяций эволюционирует таким образом, что его средний мальтузианский параметр всегда возрастает, достигая в устойчивом равновесии максимума [19].
Применение методов математической статистики и теории вероятностей позволяет изучить вопрос о реализации принципа максимума мальтузианского параметра (в предположении, что постулат справедлив) за счет изменения структуры сообщества. Так, в цитируемой работе определены вектор, задающий структуру сообщества в устойчивом равновесии, и вероятность этого равновесия. Кроме того, возможно разделение структур на вероятные и маловероятные. Получены условия, при которых в процессе адаптации из сообщества эллиминируютия все виды, кроме одного или ни один вид из сообщества не исключается.
ЭКСТРЕМАЛЬНЫЕ СВОЙСТВА СООБЩЕСТВА С ГОРИЗОНТАЛЬНОЙ СТРУКТУРОЙ
В данном разделе описан несколько иной взгляд на применение экстремальных принципов. Заключается он в получении из динамических уравнений соотношений, которые можно интерпретировать как экстремальные принципы [20]. В основе такого подхода лежит исследование так называемых вольтерровских моделей сообществ, описываемых системой уравнений
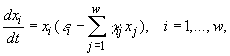
где ![]() – скорость естественного прироста или смертности i-го вида в отсутствие всех остальных видов, а знак и абсолютная величина
– скорость естественного прироста или смертности i-го вида в отсутствие всех остальных видов, а знак и абсолютная величина ![]() отражает соответственно характер и интенсивность влияния j-го вида на i-й вид,
отражает соответственно характер и интенсивность влияния j-го вида на i-й вид, ![]() – показатель внутривидового взаимодействия для i-го вида. В терминах частот (относительных численностей)
– показатель внутривидового взаимодействия для i-го вида. В терминах частот (относительных численностей) ![]()
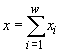 уравнения динамики сообщества имеют вид
уравнения динамики сообщества имеют вид

где 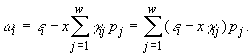 Рассматривается сообщество с горизонтальной структурой, т.е. сообщество, состоящее из видов, расположенных на одном трофическом уровне и конкурирующих за один или несколько ресурсов, что означает выполнение равенств
Рассматривается сообщество с горизонтальной структурой, т.е. сообщество, состоящее из видов, расположенных на одном трофическом уровне и конкурирующих за один или несколько ресурсов, что означает выполнение равенств ![]() .
.
Вектор ![]() с координатами
с координатами ![]() ,
, ![]() называют композицией сообщества. Множество возможных композиций – симплекс
называют композицией сообщества. Множество возможных композиций – симплекс ![]() в положительном ортанте n-мерного пространства. Вектор
в положительном ортанте n-мерного пространства. Вектор ![]() – равновесная композиция, определяемая из условия
– равновесная композиция, определяемая из условия ![]() Показано, что между численностью x и равновесной композицией существует взаимнооднозначное соответствие.
Показано, что между численностью x и равновесной композицией существует взаимнооднозначное соответствие.
Представление уравнений вольтерровской модели в частотной форме позволяет выделить в общем процессе эволюции сообщества два да известной степени различных, хотя и связанных процесса: эволюция композиции и эволюция общей численности. Естественно, что скорости этих процессов могут быть различны.
Вводится функция 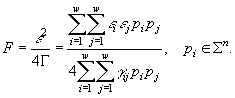 Здесь ε – средний коэффициент естественного прироста для всего сообщества в целом, Г – средний коэффициент конкуренции. Исследование экстремумов функции F дает следующий результат: равновесная композиция
Здесь ε – средний коэффициент естественного прироста для всего сообщества в целом, Г – средний коэффициент конкуренции. Исследование экстремумов функции F дает следующий результат: равновесная композиция ![]() является экстремальной точкой и
является экстремальной точкой и ![]() Функция F может быть интерпретирована как мощность сообщества или мера скорости протекания энергии. Таким образом, формулируется экстремальный принцип: сообщество видов, конкурирующих за один или несколько ресурсов, эволюционирует в сторону увеличения мощности или скорости протекания через него энергии, причем в равновесии эта мощность (или скорость) максимальна.
Функция F может быть интерпретирована как мощность сообщества или мера скорости протекания энергии. Таким образом, формулируется экстремальный принцип: сообщество видов, конкурирующих за один или несколько ресурсов, эволюционирует в сторону увеличения мощности или скорости протекания через него энергии, причем в равновесии эта мощность (или скорость) максимальна.
Однако, этот принцип не говорит о характере (монотонности) эволюции и ее скорости, он является локальным.
Исследование функции 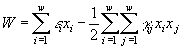 демонстрирует существование глобального максимума и единственного устойчивого состояния равновесия системы
демонстрирует существование глобального максимума и единственного устойчивого состояния равновесия системы 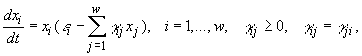 причем любая, начинающаяся внутри положительного ортанта, траектория системы при
причем любая, начинающаяся внутри положительного ортанта, траектория системы при ![]() стремится к данному равновесию. В том случае, когда максимум функции W не достигается внутри положительного ортанта, он будет достигаться на его границе на соответствующих координатных гиперплоскостях. Это означает, что в процессе эволюции экосистемы один или несколько видов должны элиминироваться, поскольку такое равновесное состояние снова будет устойчивым.
стремится к данному равновесию. В том случае, когда максимум функции W не достигается внутри положительного ортанта, он будет достигаться на его границе на соответствующих координатных гиперплоскостях. Это означает, что в процессе эволюции экосистемы один или несколько видов должны элиминироваться, поскольку такое равновесное состояние снова будет устойчивым.
Функция W может быть интерпретирована как разница между репродуктивным потенциалом сообщества ![]() и общими затратами на конкуренцию (на дыхание экосистемы)
и общими затратами на конкуренцию (на дыхание экосистемы) 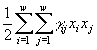 . Тогда возрастание функции W означает стремление системы максимизировать указанную разницу, что можно сделать либо максимизируя репродуктивный потенциал при заданных тратах на конкуренцию, либо минимизируя затраты на конкуренцию при ограниченном репродуктивном потенциале (существуют и промежуточные ситуации). В природе этим двум противоположным механизмам соответствуют, так называемые, r-конкуренция и K - конкуренция.
. Тогда возрастание функции W означает стремление системы максимизировать указанную разницу, что можно сделать либо максимизируя репродуктивный потенциал при заданных тратах на конкуренцию, либо минимизируя затраты на конкуренцию при ограниченном репродуктивном потенциале (существуют и промежуточные ситуации). В природе этим двум противоположным механизмам соответствуют, так называемые, r-конкуренция и K - конкуренция.
Привлечение понятия жизненного пространства, в которое включены все важные для особей сообщества факторы среды, и исследование соответствующих функций, формализующих данное понятие, позволило сформулировать следующий принцип. Сообщество конкурирующих за жизненное пространство видов эволюционирует к состоянию с максимально плотной упаковкой, причем в процессе эволюции плотность упаковки сообщества всегда возрастает, достигая в равновесном состоянии максимально возможного для данной среды значения. (В качестве меры плотности упаковки рассматривается среднеквадратическая разность между реально существующим и необходимым для сообщества жизненным пространством. Чем меньше эта разность, тем плотнее упакованы виды.)
Исследование вольтерровских систем общего вида, т.е. где ![]() могут иметь любой знак, а на коэффициенты
могут иметь любой знак, а на коэффициенты ![]() не наложено никаких ограничений, позволило авторам дать следующую интерпретацию результатов: при эволюции сообщества к устойчивому нетривиальному равновесию (
не наложено никаких ограничений, позволило авторам дать следующую интерпретацию результатов: при эволюции сообщества к устойчивому нетривиальному равновесию (![]() ) скорость увеличения его равновесного разнообразия
) скорость увеличения его равновесного разнообразия ![]() должна быть по крайней мере не меньше скорости прироста общей численности (или биомассы).
должна быть по крайней мере не меньше скорости прироста общей численности (или биомассы).
ПРИНЦИП МАКСИМУМА ИСПОЛЬЗОВАННОЙ ЭНЕРГИИ
Н.С.Печуркин [16] предложил энергетический принцип экстенсивного развития, согласно которому, в процессах биологического развития надорганизменных систем (эволюции, экологических сукцессиях и перестройках) величина использованного биологической потока энергии возрастает, достигая локальных максимальных значений в стационарных состояниях.
Обозначив через Hпад величину потока падающей энергии, т.е. потока энергии, который потенциально может быть использован некоторой биологической системой, через Hисп – ту часть потока, которую система захватывает и использует, через Hнеисп – неиспользованную часть потока (Hпад= Hисп+ Hнеисп), сформулированный энергетический принцип можно записать в виде:
![]() или
или ![]()
Учитывая, что поток энергии, захваченный системой складывается из доли, связанной с запасами энергии в активной биомассе В, и потерь на дыхание системы R (![]() , μ – показатель прироста биомассы), критерий для внутреннего распределения энергии запишется в виде
, μ – показатель прироста биомассы), критерий для внутреннего распределения энергии запишется в виде![]()
Кинетическое обоснование принципа экстенсивного развития было проведено для модели динамики микробных популяций, эволюционирующих в условиях проточного культивирования. Существование отбора показано при введении двух типов селекционных ограничений: постоянной общей организации и постоянного общего потока. Экспериментальной эволюционной системой, соответствующей условию постоянных потоков, является хемостат, в котором развивается генетически неоднородная популяция микроорганизмов. Система уравнений, описывающих эту ситуацию, имеет вид
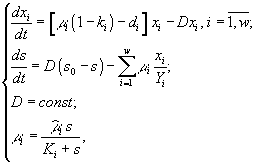 (17)
(17)
где (1 – ki) – доля точных копий в поколении i-й формы; m i – удельная скорость роста i-й формы микроорганизма; di – удельная скорость отмирания i-й формы;
xi – концентрация i-й формы; D – удельная скорость разбавления; s – концентрация лимитирующего субстрата; s0 – концентрация субстрата во входном потоке; Yi – коэффициенты, определяющие потребление субстрата на прирост биомассы; ![]() – константы полунасыщения.
– константы полунасыщения.
Второе уравнение системы (17) можно записать на языке потоков энергии:
![]()
В условиях сильного лимитирования (![]() , где
, где ![]() – все виды элиминации исходной формы) для стационарного состояния выполняется соотношение
– все виды элиминации исходной формы) для стационарного состояния выполняется соотношение
![]()
Появление мутанта с повышенной скоростью роста ![]() будет приводить к его накоплению и снижению концентрации лимитирующего субстрата в стационарном состоянии
будет приводить к его накоплению и снижению концентрации лимитирующего субстрата в стационарном состоянии ![]() . Снижение величины
. Снижение величины ![]() будет вызывать накопление мутантов со сниженной константой полунасыщения
будет вызывать накопление мутантов со сниженной константой полунасыщения ![]() , уменьшенной скоростью отмирания dm < di и пониженной частотой мутирования km < ki. При появлении следующего, более активного мутанта будет происходить переход к еще более низкой стационарной величине
, уменьшенной скоростью отмирания dm < di и пониженной частотой мутирования km < ki. При появлении следующего, более активного мутанта будет происходить переход к еще более низкой стационарной величине![]() . Поскольку скорость протока D остается неизменной, будет возрастать степень использования субстрата. В этом можно убедиться, записав стационарное состояние для второго уравнения системы (17)
. Поскольку скорость протока D остается неизменной, будет возрастать степень использования субстрата. В этом можно убедиться, записав стационарное состояние для второго уравнения системы (17) ![]() на языке потоков энергии
на языке потоков энергии![]() Таким образом, величина Ннеисп снижается и при неизменном значении Нпад увеличивается величина Нисп, т.е. для системы с постоянными потоками выполняется принцип экстенсивного развития.
Таким образом, величина Ннеисп снижается и при неизменном значении Нпад увеличивается величина Нисп, т.е. для системы с постоянными потоками выполняется принцип экстенсивного развития.
Для системы с постоянной организацией (типа турбидостата) динамика описывается уравнениями
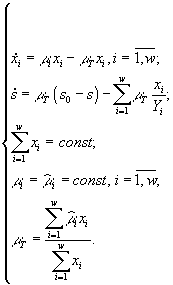
Балансовое уравнение потоков имеет вид ![]() или
или ![]() В результате эволюции системы увеличивается скорость разбавления m
Т при сохранении концентрации биомассы, а, значит, и возрастает поток использованной энергии. Хотя поток неиспользованной энергии тоже будет возрастать (значение
В результате эволюции системы увеличивается скорость разбавления m
Т при сохранении концентрации биомассы, а, значит, и возрастает поток использованной энергии. Хотя поток неиспользованной энергии тоже будет возрастать (значение ![]() не меняется согласно уравнению для стационарного состояния
не меняется согласно уравнению для стационарного состояния ![]() ), его прирост будет компенсирован гораздо большим возрастанием потока падающей энергии.
), его прирост будет компенсирован гораздо большим возрастанием потока падающей энергии.
В той же работе Н.С.Печуркин сформулировал энергетический принцип интенсивного развития: любая живая система надорганизменного уровня развивается (эволюционирует) таким образом, что поток использованной энергии на единицу биологической структуры за время ее существования возрастает.
Показатель уровня интенсивного энергетического развития ![]() может быть записан в виде
может быть записан в виде ![]() . Если за время генерации принять время удвоения биомассы, то
. Если за время генерации принять время удвоения биомассы, то ![]() (g – длительность поколения).
(g – длительность поколения).
Для меняющегося потока 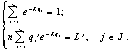 , где Нисп(t) – мгновенное значение потока энергии.
, где Нисп(t) – мгновенное значение потока энергии.
Для демонстрации выполнения сформулированного принципа приводятся следующие примеры:
1) для микроорганизмов ![]() 1,7 – 2,3;
1,7 – 2,3;
для растений ![]() 1,82;
1,82;
для насекомых ![]() 7 – 10;
7 – 10;
для млекопитающих ![]() 50 – 100;
50 – 100;
2) зависимость интенсивности теплорассеяния Q от веса организма M описывается уравнением: ![]() , a, k – константы. Коэффициент a, характеризующий интенсивность энергообмена, в процессе эволюции существенно возрастает: для одноклеточных а = 0,084 кал/ч, для пойкилотермных животных а = 0,69 кал/ч, для гомойтермных а = 19,68 кал/ч.
, a, k – константы. Коэффициент a, характеризующий интенсивность энергообмена, в процессе эволюции существенно возрастает: для одноклеточных а = 0,084 кал/ч, для пойкилотермных животных а = 0,69 кал/ч, для гомойтермных а = 19,68 кал/ч.
Для конкретных приложений (например, к классификации в пределах вида или рода) применимость энергетического принципа интенсивного развития как универсального критерия макроэволюции пока разработана недостаточно.
ПРИНЦИП МАКСИМАЛЬНОГО СУММАРНОГО ДЫХАНИЯ
Ф.Вашида [51] предложил гипотезу, согласно которой система стремится организовать свою биологическую конфигурацию так, чтобы максимизировать суммарное дыхание.
Для экосистемы, находящейся в стадии развития, доминирующим является рост как накопление суммарной биомассы, поэтому отношение P/R, где P – суммарная продукция экосистемы, а R – суммарное дыхание, значительно больше 1. При наступлении фазы зрелости, отношение P/R достигает 1. На этой стадии, которая является устойчивым состоянием, продукция достигает своего максимального уровня при данных условиях окружающей среды, а суммарное дыхание достигает максимального значения для данной продукции. Гипотеза максимального дыхания утверждает, что развитие экосистемы происходит так, чтобы как можно раньше достичь конфигурации, при которой дыхание максимально.
Была рассмотрена система, состоящая из двух биологических компонентов (продуцента и редуцента), единственного вида поступающей энергии (солнечная радиация), и одного питательного вещества. Продуцент потребляет солнечную энергию и ресурс, при этом увеличивает собственную биомассу и теряет тепло (дышит). Редуцент поглощает продуцента, при этом увеличивает свою биомассу, производит питательное вещество и дышит. Продуцирование и редуцирование синхронизированы во времени.
В модели приняты обозначения: x1 – количество биомассы, произведенной за некоторый период времени; x2 – количество питательного вещества, созданного за тот же период; e1, a21 – количество солнечной энергии и питательного вещества, необходимые для производства единицы продукции, соответственно; r1 – количество дыхания, генерируемое единицей продукции; a12 – количество биомассы, необходимое для производства единицы питательного вещества; b32 и r2 – соответственно масса редуцента и количество дыхания, созданное им при производстве единицы питательного вещества; p1, p3 – энергия, заключенная в единице биомассы продуцента и редуцента, соответственно; E – верхний предел солнечной радиации, которая может быть использована продуцентом; S – солнечная энергия, поступающая в систему, q – эффективность удержания этой энергии продуцентом.
Согласно первому закону термодинамики, должны выполняться следующие равенства: e1 = p1 + r1 и p1a12 = p3b32 + r2. Задача ставится следующим образом: максимизировать сумму R = r1x1 + r2x2 при условиях
e1x1 £ E = qS, a12x2 £ x1, a21x1 £ x2, 0 £ b32x2 и x1, x2 ³ 0.
Неравенства определяют область допустимых решений, среди которых ищется оптимальный набор (x1, x2). Условие, при котором существует хотя бы одно допустимое решение, имеет вид a12 a21 £ 1 – количество биомассы, косвенно необходимое для производства его же, должно быть меньше 1. Если это условие не выполнено, экосистема не может поддерживать состояние равновесия.
Область допустимых решений представлена на рис. 3 (треугольник АОВ). Поскольку величины r1 и r2 положительны, то требованию максимальности общего дыхания R удовлетворяет набор (x1, x2), соответствующий точке А. Биологически это означает, что редуцент перерабатывает всю биомассу, и питательное вещество возмещается в излишке.
Также была рассмотрена более сложная система, в которую входит два редуцента, потребляющих и выделяющих одни и те же вещества, только в разных соотношениях, т.е. их экологические ниши не идентичны, но сильно пересекаются. Питательные вещества, производимые редуцентами, полностью взаимозаменяемы.
Коэффициенты, относящиеся ко второму редуценту, обозначены буквами с верхним индексом “*”.
Энергетические соотношения в новой модели записываются равенствами e1 = p1+r1, p1a12 = p3b32+r2, p1a12* = p3b32*+r2*.
Задача максимального дыхания описывается следующими выражениями r1x1+r2x2+r2*x2*® max, e1x1 £ E, a12x2+a12*x2* £ x1, a21x1 £ x2+x2*, 0 £ b32x2+b32*x2*, x1, x2, x2* ³ 0.
Задача требует рассмотрения двух случаев.
1) Каждый из редуцентов способен в одиночку поддерживать систему. Математически это означает выполнение двух неравенств:
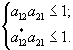
В этом случае решение задачи зависит от того, какой из редуцентов дает больший вклад в общее дыхание системы. Если ![]() >
> ![]() , то решение: x2 = 0,
, то решение: x2 = 0, ![]() > 0, иначе –x2 > 0,
> 0, иначе –x2 > 0, ![]() = 0 (равенство отношений означает эквивалентность редуцентов). После исключения одного из редуцентов задача сводится к предыдущей.
= 0 (равенство отношений означает эквивалентность редуцентов). После исключения одного из редуцентов задача сводится к предыдущей.
2) Новый редуцент не в состоянии в одиночку поддерживать систему, т е.

Если при этом он менее эффективен в выработке дыхания, то происходит его исключение из экосистемы. Содержательная ситуация имеет место при выполнении условия ![]() >
> ![]() .
.
Область допустимых решений представляет собой пирамиду АВСО (рис.4). Максимум дыхания достигается при наборе (x1, x2, x2*), соответствующем точке А. При таких значениях биомасс x1, x2, x2* солнечная энергия полностью перерабатывается и уровень производства питательного вещества и биомассы продуцента максимальны. Почему решением является именно точка А, ведь в этом случае первый редуцент должен снизить свой уровень активности “в угоду” новому и “в ущерб” себе? Рассматриваемая модель находится в устойчивом состоянии, согласно гипотезе максимального дыхания, система реорганизует свою конфигурацию для максимизирования дыхания, а это значит, что она стремится увеличить эффективность переработки энергии (на зрелом уровне это уже не накопление биомассы). Низкая эффективность использования энергии идентична уязвимости системы. Естественный отбор экосистем генерирует таких индивидов, которые объединяются для существования экосистемы даже ценой уменьшения численности их собственной популяции. Таким образом, стабильность экосистемы с максимальным уровнем дыхания гарантируется эволюцией.
На основании принципа максимального суммарного дыхания автор моделирует луговую экосистему. Модель состоит из 19 компонент и 16 видов энергетических и материальных потоков, связанных с компонентами. Компоненты разделены на 3 группы: продуценты, гетеротрофы — 3 вида травоядных и 3 вида плотоядных — и редуценты (12 составляющих). Энергетические и материальные потоки включают солнечную энергию, мертвую материю и другие аналогичные составляющие.
В результате исследования соответствующей вариационной задачи были получены следующие выводы:
Автор приходит к выводу, что используемая им модель достаточно адекватно описывает зрелые луговые экосистемы.
МОДЕЛИ ДИНАМИЧЕСКОЙ СТРУКТУРЫ
В последнее время широкое распространение получило использование так называемой модели динамической структуры. Необходимость применения такого рода моделей обоснована в работах С.Йоргенсена с соавторами [32, 25]. Экосистемы и их живые компоненты способны изменять свои свойства с изменением внешних условий, причем регулирующие процессы могут проходить на индивидуальном (адаптация) и на экосистемном (изменение видов и структуры) уровне. Поэтому для описания взаимосвязи между состоянием системы и внешними по отношению к ней факторами необходимо заложить в используемые модели соответствующие экологические законы, позволяющие учесть изменения в составе и (или) структуре системы.
Модель динамической структуры определяется как математическая модель, в рамках которой возможно изменение величины параметров, в соответствии с выбранной целевой функцией [25]. В отличие от традиционных моделей, в которых имитация действительной ситуации, описываемой экспериментальными данными, идет за счет минимизации суммы разниц между вычисленными и экспериментальными значениями переменных состояния, модели динамической структуры подбираются под реальную картину в результате поиска наилучшей комбинации параметров, которая максимизирует целевую функцию. Ключевой момент такой модели – выбор набора параметров среди большого количества, использующегося в традиционных моделях, и выбор целевой функции, которая наилучшим образом описывает развитие экосистемы. Описание целевых функций, которые в разное время предлагались для применения в экстремальных моделях, приведено в ряде работ [42, 31, 32], по которым ведется дальнейшее цитирование.
Общий поток энергии через систему (Total system throughflow of energy) – первая из характеристик системы, предложенная в качестве целевой функции – задается выражением 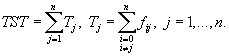 Tj представляет собой общий поток энергии (вещества) из j-ой части системы, fij – поток от j к i, значение индекса i = 0 обозначает внешнюю среду. Согласно принципу максимума мощности, который был развит Х.Одумом и Р.Пинкертоном [40], функционирование экосистемы происходит так, чтобы максимизировать мощность, т.е., говоря математическим языком, в данной модели требуется максимизировать скорость изменения величины TST. (В случае дискретного времени рассматриваются члены
Tj представляет собой общий поток энергии (вещества) из j-ой части системы, fij – поток от j к i, значение индекса i = 0 обозначает внешнюю среду. Согласно принципу максимума мощности, который был развит Х.Одумом и Р.Пинкертоном [40], функционирование экосистемы происходит так, чтобы максимизировать мощность, т.е., говоря математическим языком, в данной модели требуется максимизировать скорость изменения величины TST. (В случае дискретного времени рассматриваются члены ![]() где
где ![]() – временной интервал.)
– временной интервал.)
Во всеобъемлющей теории роста и развития экосистемы, предложенной Р.Улановичем [48], роль целевой функции выполняет асценденция  . Максимизация этой функции должна описывать автокаталитические тенденции, присущие организации развития экологических сетей.
. Максимизация этой функции должна описывать автокаталитические тенденции, присущие организации развития экологических сетей.
Эмержентность была предложена на роль целевой функции Х.Одумом [39]. Это качественный фактор энергии, измеряющий удаленность данного типа энергии от первоначальной солнечной энергии. Например, энергия топлива более высокого качества, чем солнечная энергия. 104 калорий солнечной энергии производят 102 калорий первичных продуцентов, которые, в свою очередь, производят 10 калорий хищников. Если принять качество солнечной энергии за единицу, то качество более высоких трофических уровней соответственно будет 100, 1000, 10000.
В последнее время наиболее широкое распространение получила функция эксергии или энергии перехода (Ex), которую понимают как максимальную свободную энергию, которую система способна выделить в пространство при переходе в состояние термодинамического равновесия [31]. Эксергия определяется окружающей систему средой и может быть рассмотрена как мера термодинамического порядка. Кроме того, энергия перехода непосредственно связана термодинамической информацией I: Ex = IT (T – температура). Для систем с неорганическими потоками и пассивным продуцированием органических веществ энергия перехода задается выражением  где R – газовая постоянная; T – абсолютная температура; ci - концентрация в экосистеме i-го компонента; cieq – соответствующая концентрация i-го компонента в термодинамическом равновесии; индекс i = 0 отвечает неорганическим компонентам рассматриваемого химического вещества. С.Йоргенсен и Х.Мэйер предлагают следующую формулировку термодинамического закона экологии: экосистема стремится ответить на изменения внешних факторов путем формирования нового состава (а может быть даже и новой структуры), максимизирующего при определяемых внешними факторами условиях величину энергии перехода [31].
где R – газовая постоянная; T – абсолютная температура; ci - концентрация в экосистеме i-го компонента; cieq – соответствующая концентрация i-го компонента в термодинамическом равновесии; индекс i = 0 отвечает неорганическим компонентам рассматриваемого химического вещества. С.Йоргенсен и Х.Мэйер предлагают следующую формулировку термодинамического закона экологии: экосистема стремится ответить на изменения внешних факторов путем формирования нового состава (а может быть даже и новой структуры), максимизирующего при определяемых внешними факторами условиях величину энергии перехода [31].
К.Паттен [41, 42] предложил экстремальный принцип, согласно которому процессы самоорганизации в экосистеме происходит в направлении увеличения косвенных эффектов.
Все перечисленные целевые функции описываются в терминах энергии и сложности экосистемы, что натолкнуло на мысль об их тесной взаимосвязи. В частности, К.Паттен в своей работе [42] показал, что эксергия, эмержентность, асценденция и косвенные эффекты имеют взаимосвязанную микроскопическую динамику.
В процессе упорядоченного развития сообщества экосистема достигает зрелой и стабильной стадии. Стабильность – свойство реагировать на внешние воздействия небольшим изменением биомассы и быстро возвращаться к исходному состоянию после окончания воздействия [43].
Авторы статьи предложили индекс зрелости, основанный на мере неопределенности. Неопределенность понимается как невозможность заранее знать каким будет путь данной единицы вещества или энергии в экосистеме. Было сделано предположение, что стратегия жизни фокусируется в направлении получения как можно более сложной и разнообразной структуры. По этой причине при достижении зрелости экосистема получается более сложной. Сложная система cсоответствует более высокому разнообразию и большому количеству взаимосвязей, что делает доступным большое количество путей для получения энергии в случае каких-либо изменений. В сложной системе уменьшается возможность определить путь данной единицы вещества, и неопределенность возрастает. Формула, выражающая меру неопределенности H для нескольких независимых событий, была описана Р.Улановичем [48]
![]() ,
,
где pi – вероятность исхода i, n – количество событий, K – константа пропорциональности.
Кроме неопределенности, зрелость должна быть связана с другим параметром, дающим экосистеме независимость от внешних изменений. Авторы полагают, что таким свойством является способность системы использовать ее собственный детрит. Более эффективный цикл использования детрита в системе дает более зрелую, независимую и устойчивую систему. Взяв за основу формулу, выражающую меру неопределенности и добавив потоки детрита, выводится индекс зрелости
 ,
,
где tij – поток вещества от вида i к виду j; T – сумма всех членов tij; ![]() – поток детрита к k-му виду. Чтобы представить все возможные потоки добавляется импорт (индекс 0, только выход), экспорт и дыхание (n + 1 и n + 2, только вход).
– поток детрита к k-му виду. Чтобы представить все возможные потоки добавляется импорт (индекс 0, только выход), экспорт и дыхание (n + 1 и n + 2, только вход).
ПРИНЦИП НАИМЕНЬШЕЙ ДИССИПАЦИИ ЭНЕРГИИ И НАИСКОРЕЙШЕГО СПУСКА
В основе исследований А.И.Зотина и А.А.Зотина в области макроэволюционных изменений лежит термодинамика, которая является общей феноменологической теорией любых процессов и явлений, протекающих в природе, сопровождающихся диссипацией энергии, т.е. возникновением энтропии [2]. Согласно предложенному принципу наименьшей диссипации энергии в устойчивом состоянии любой термодинамической системы скорость диссипации энергии в ней минимальна. Этот новый термодинамический принцип включает в себя второе начало термодинамики и охватывает практически все явления природы [2].
Указанный принцип является конечной характеристикой равновесного состояния. Для описания самого переходного процесса формулируется принцип наискорейшего спуска: в процессе приближения термодинамической системы к равновесному или стационарному состоянию функция внешней диссипации убывает наискорейшим возможным способом [2].
ЗАКЛЮЧЕНИЕ
Подводя итоги проделанному обзору следует констатировать огромное разнообразие мнений и подходов в попытках ответить на вопрос "Что экстремально в биологических системах?" Это разнообразие обязано как многоуровневости объектов биологии, так и отсутствию методологической унификации в выборе экстремальных принципов и ограничивающих экстремумы условий. Успешное развитие вариационного моделирования требует, по-видимому, решения методологических проблем:
***
Работа выполнена при поддержке Российского фонда фундаментальных исследований (грант №02-04-48085 и №02-04-06044).
СПИСОК ЛИТЕРАТУРЫ
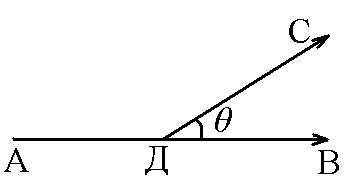
Рис.1. Отхождение бокового сосуда от основного ствола. q – угол ответвления

Рис.2. Разветвление сосудов
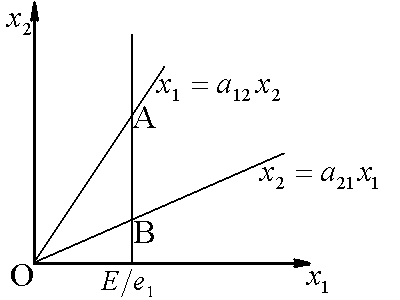
Рис.3. Область допустимых решений (OAB) задачи для системы продуцент – редуцент. x1 – количество биомассы, произведенной за некоторый период времени; x2 – количество питательного вещества, созданного за тот же период; e1, a21 – количество солнечной энергии и питательного вещества, необходимые для производства единицы продукции, соответственно; a12 – количество биомассы, необходимое для производства единицы питательного вещества; E – верхний предел солнечной радиации, которая может быть использована продуцентом
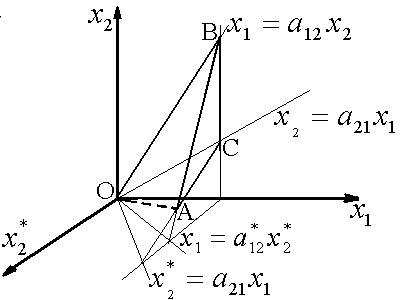
Рис.4. Область допустимых решений (OABC) задачи для системы продуцент – два редуцента. x1 – количество биомассы, произведенной за некоторый период времени; x2 – количество питательного вещества, созданного за тот же период; e1, a21 – количество солнечной энергии и питательного вещества, необходимые для производства единицы продукции, соответственно; a12 – количество биомассы, необходимое для производства единицы питательного вещества. Коэффициенты, относящиеся ко второму редуценту, обозначены буквами с верхним индексом “*”
Аннотация
В обзоре представлены экстремальные принципы, применяемые в различных областях биологии. Рассмотрен широкий спектр задач, от механизма протекания биохимических реакций в клетках до эволюции надорганизменных систем. Описано решение вопросов, связанных с конструкцией организма, энергетическими затратами как отдельных органов, так и индивида в целом. Приведено применение экстремальных принципов в изучении развития отдельных популяций и структуры сообществ.
Extremal principles application in mathematical biology: scientific review
P.V.Fursova, A.P.Levich, V.L.Alexeyev
Moscow State University, Biology faculty, Moscow
Abstract
In the review extreme principles applications in various areas of biology are submitted. The wide spectrum of tasks, from the mechanism of course of biochemical reactions in cells to systems evolution is considered. The decision of questions connected to organism design, power expenses both in organs, and individual as a whole is described. The application of extreme principles in study of development of separate populations and structure of communities is given.