Г. А. Голицын, А. П. Левич

Принцип максимума информации и вариационные принципы в НАУЧНОМ ЗНАНИИ*

Введение

В методах научного описания мира существует крайне ограниченный набор формальных способов вводить основные законы изменчивости исследуемых систем. Почти всегда такие законы постулированы или в форме уравнений движения, или в форме экстремального принципа. Как правило, такие формулировки равносильны: если имеется уравнение движения, то из его вида может быть выведен функционал, для которого исходное уравнение является уравнением Эйлера-Лагранжа соответствующей вариационной задачи, и наоборот. Однако, экстремальные принципы обладают большей эвристической и обобщающей силой. Поясню сказанное простым примером. Почему камень, брошенный под углом к горизонту, движется по параболе? Можно указать на квадратичное уравнение равнопеременного движения тела. Само это уравнение составляет следствие второго закона Ньютона для тела, движущегося под действием постоянной силы. Впрочем, парабола может быть представлена и геодезической линией – решением уравнений Эйнштейна из общей теории относительности для движений в сильных полях и с высокими скоростями. Закон Ньютона и уравнения Эйнштейна могут быть выведены из принципа наименьшего действия с определенной формой экстремизируемого лагранжиана. Таким образом, существует несколько уровней объяснения явлений, каждый из которых может служить исходным постулатом. Однако, уравнения равнопеременного движения относятся лишь к узкому классу явлений, второй закон Ньютона описывает все движения в несильных полях и с невысокими скоростями, уравнения Эйнштейна лишены этих ограничений, а принцип наименьшего действия применим ко всем формам механического и электромагнитного движений.

В кратком обзоре невозможно охватить все богатство и разнообразие идей, связанных с вариационными принципами. Необходима какая-то руководящая идея для отбора материала. Такой идеей служит для нас желание получить в руки какой-то метод формулировки вариационных принципов для новых областей научного знания.

Информация как структура систем

Для классифицирования некоторых подходов к описанию процесса информации удобно представить традиционную трехчленную цепочку: передатчик – код – приемник, в форме (Левич, 1978):

структура объекта – отображение – тезаурус приемника

Большинство подходов, изучающих понятие информации, оперирует лишь с частью членов этой, необходимо целостной, цепочки. Так, устойчивая традиция философской литературы, трактуя информацию как "отраженное разнообразие" (Бирюков, 1974) в основном, изучает свойства отображения и структуры объекта. Работы М.Мазура (Мазур, 1974) и А.А.Шарова (Шаров, 1976) называют информацией и исследуют отображения, перекодировки структур. В семантическом подходе к понятию информации Ю.А.Шрейдера (Шрейдер, 1967) информация понимается в ракурсе изменений тезауруса приемника. Алгоритмический подход (Колмогоров, 1965) охватывает как способ отображения фрагмента реальности – эффективную процедуру, так и весьма специальную форму тезауруса приемника – алгоритм, вычисляемый машиной Тьюринга. Тем самым информация и ее количество – длина алгоритма – оказываются свойствами тезауруса приемника. Весьма распространено понимание информации как самой структуры изучаемых объектов. Фактически так поступает К.Шеннон (Шеннон, 1963), задавая структуру объекта вероятностной мерой на его элементах. Н.Рашевский (Rashewski, 1955) и, обобщая его, Ю.А.Шрейдер (Шрейдер, 1974) вычисляют количество информации, содержащейся в модели, т. е. в математической структуре множества с отношениями, и, очевидно, подразумевают, что сама структура и есть информация. В подходах, обозначаемых "информация без вероятности" (Ingarten, Urbanik, 1962; Cerny, Brunovsky, 1974; Urbanik, 1974), строится отображение в множество действительных чисел, некоторой математической структуры (например, "лестницы" из булевых колец). Образ этого оператора называется количеством информации. Тем самым, под информацией можно понимать область отправления оператора, или исходную математическую структуру.

Приведем примеры, конкретизирующие общую схему феномена информации: 1) объектом будем считать окружающий мир, отображением – первую или вторую сигнальную систему, приемником – тезаурус субъекта; 2) субъект – речь или текст – субъект; 3) предок – генетический код – потомок; 4) фрагмент реальности – язык программирования – тезаурус логической машины; 5) среда – экологический код (Левич, 1983) – экологическое сообщество. В приведенных примерах обращает на себя внимание факт обязательной включенности в информационный процесс языковой структуры (сигнальная система, текст, генетический или экологический код). Этот факт указывает на сложность целостного феномена информации, поскольку в качестве составной части в него входит столь мощная система как язык. Наибольшей перспективностью и, вместе с тем, трудностью на пути целостной экспликации феномена информации, видимо, обладают подходы, охватывающие семантический участок процесса – тезаурус приемника. Однако настоящая работа касается наиболее доступной части явления – структуры систем, выступающей в роли источника информации.

Терминология информатики не устоялась; предшествующий, более чем беглый, обзор некоторых подходов в теории информации показывает, что термином "информация" называют и образ структуры системы при отображении в действительные числа, и морфизмы, осуществляющие отражение одних структур в другие, и состояние тезауруса приемника. Поэтому полезно сразу оговорить употребление терминов в предлагаемой читателю работе. В следующих ее разделах будут последовательно введены такие понятия, как структура системы и инвариант структуры – образ определенного представления из совокупности систем в числовое множество. Так, под информацией, содержащейся в системе, будем понимать структуру системы; инвариант структуры станем называть количеством такой информации; соответствия, осуществляющие отражение системы в тезаурус приемника, будем именовать информационными морфизмами и структуру тезауруса приемника – семантической информацией.

Понятие "структура", заменившее в настоящей работе понятие "информация", само весьма полиморфно и требует четкой экспликации. Прежде чем заняться ею, рассмотрим несколько примеров сложившейся практики описания структур естественнонаучных систем. Так, экологическое сообщество из особей различных видов удобно представить структурой множества с разбиениями, где классы разбиения как раз соответствуют слагающим сообщество популяциям. Множеством с разбиением можно описывать распределение по энергиям частиц газа или выделение из текста групп, составленных из сходных словоформ. Социальная или таксономическая иерархия могут быть представлены как теоретико-множественная совокупность булеанов с включением или иным отношением порядка. Понятие близости-удаленности точек в нашем эмпирическом или априорном представлении о пространстве описывают топологической структурой, а "голосующие системы" удовлетворяют аксиомам абстрактной структуры большинства (Виленкин, Шрейдер, 1976). Совокупность состояний электрона в атоме можно описывать структурой гильбертова пространства или равносильным образом – полем бесконечномерных матриц.

Из приведенных примеров видно, что под структурами имеют в виду математические структуры, как они понимаются, например, у Н.Бурбаки (Бурбаки, 1965) или И.Букура и А.Деляну (Букур, Деляну, 1972). Удобным языком для формализации понятия "математическая структура" является язык теории категорий (Букур, Деляну, 1972; Цаленко, Шульгейфер, 1974; Blanchard, 1974). И в последующем изложении под структурой естественной системы будем понимать структуру объекта из описывающей систему категории, например, структуру конкретного множества с отношениями, структуру определенной группы или структуру фиксированного топологического пространства (Левич, 1982).

Таким образом, система эксплицирована категорией, объекты которой должны быть интерпретированы как состояния системы. Существенной чертой категорного описания систем является необходимость задавать не только возможные состояния системы, но и допустимые способы преобразования одних состояний в другие – морфизмы категории. Причем категории с совпадающими объектами, но различающимися морфизмами, строго говоря, изображают различные системы. Например, систему, описываемую множествами с произвольными отображениями друг в друга, мы будем отличать от системы, где те же множества преобразуются лишь взаимно однозначно. Процессы, происходящие в первой системе, богаче, чем во второй, – в ней допустимы переходы между состояниями с переменным числом элементов, в то время как во второй системе осуществляются переходы только между равномощными множествами. Сам взгляд на систему как на категорию достаточно обоснован (Акчурин, 1974; Шрейдер, 1973). Задавая систему категорией, мы, однако, не фиксируем однозначно структуры объектов: в категории могут существовать объекты, только "с виду" отличающиеся друг от друга, но обладающие одинаковой структурой, например, объекты, переходящие друг в друга при переобозначениях элементов. Среди морфизмов категории могут встретиться и не отличимые друг от друга морфизмы, например, из-за каких-либо свойств симметрии отображаемых элементов. Так что, задав категорию аксиоматикой ее объектов (отношения, топологии, законы композиции и т. д.) и набором допустимых морфизмов, мы фиксируем лишь как бы "предструктуру" системы. Следует научиться сравнивать структуры состояний и способы перехода между собой и отличать подобные и неодинаковые структуры. Другими словами, удобно иметь отношение порядка и отношение эквивалентности на эксплицирующей систему категории. Обычный способ сравнения математических структур – сравнение с помощью гомоморфизмов: объявляется, что структура объекта А слабее структуры объекта В, если существует определенного вида гомоморфизм структуры из А в В; если же указанные гомоморфизмы существуют как из А в В, так и из В в А, то структуры А и В одинаковы. Например, мощность множества А меньше мощности множества В, если существует инъекция из А в В, если же существуют как инъекция из А в В, так и инъекция из В в А, то в силу принципа трихотомии существует биекция между А и В, и эти множества оказываются равномощными. Мощности множеств являются типичным примером предлагаемой конструкции структуры (предструктура – категория множеств с соответствиями в качестве морфизмов, специальные гомоморфизмы – мономорфизмы этой категории, или инъекции, структура – мощности, или кардинальные числа множеств). Именно такой подход (Левич, 1982) положен в основу конструкции сравнения структур, используемой в настоящей работе.

Еще одно соображение, проясняющее эту конструкцию, связано с тем обстоятельством, что с алгебраической точки зрения произвольная категория является частичной полугруппой, и поэтому представляется естественным вводить отношение эквивалентности на категории через факторизацию по некоторой ее подкатегории. Тем более, что аналогия с группами (теорема 1.6.3, Бурбаки, 1962) не исключает возможности, будто любое отношение эквивалентности, согласованное с композицией в полугруппе, сводится к факторизации по некоторой "нормальной" подкатегории.

Существует еще одна математическая конструкция, которая может служить инструментом сравнения структур. Если гомоморфизмы связывают "однотипные" структуры – в нашем случае объекты некоторой категории, – то представление одной категории в другую позволяет сравнивать структуры, порождаемые различной аксиоматикой. В частности, с помощью представлений мы можем исследовать объекты незнакомой природы средствами аналитически хорошо разработанных структур. Так, к примеру, физические объекты с различными типами симметрии описывают представлениями в группу матриц. Этот же методологический прием – представление исследуемой структуры в структуру хорошо известных числовых множеств – лежит в основе всех количественных описаний систем и явлений. Предлагается с помощью представлений свести сравнение произвольных структур к упорядочению кардинальных чисел и, главное, указать условия, достаточные для этого. Такая возможность заложена в самой конструкции, категорий. Дело в том, что по определению произвольной категории, каждой паре ее объектов (А, В) сопоставляется объект из категории множеств – множество морфизмов Ноm (А, В), и мощность множеств, тем самым, можно сделать универсальным инструментом сравнения категорных структур.

Основной результат изучения представления из произвольной категории в кардинальную структуру множеств состоит в следующем (Левич, 1982). Мощность Card Ноm (А, В) множества Ноm (А, В) всех морфизмов из А в В – одинакова для объектов с совпадающей структурой (и поэтому названа инвариантом структуры), а для несовпадающих структур числа Card Hom (А, В) упорядочены так же, как сами структуры: большей структуре соответствует большее число. Для согласованности упорядочения структур и чисел достаточно, чтобы гомоморфизмы, с помощью которых мы сравниваем структуры объектов, определенным образом соотносились с мономорфизмами категории. Прежде, чем перейти к эксплуатации факта существования инвариантов у структур, хотелось бы дать несколько менее специализированную переформулировку определения инварианта, которая поможет уяснить смысл не искушенному в категорной терминологии читателю: инвариант Card Hom (A, В) есть просто число сохраняющих систему преобразований состояния А в состояние В. Категорный подход лишь позволил нам формализовать понятия "система", "преобразование" и показать, собственно, инвариантность такого числа для одинаковых структур.

Еще одно методологическое замечание относится к той части математизации знаний, которая связана с внедрением количественных методов. Категорная экспликация позволяет описывать системы с самыми различными видами структур, порою весьма далекими от структур числовых множеств. Универсальность используемого в настоящей работе представления (основного функтора) в числовую структуру множеств заложена в само устройство категорий и обосновывает факт распространенности и универсальности описания систем самой различной природы числовыми характеристиками. Действительно, такое представление в кардинальную структуру множеств существует для любой категории. Одновременно становятся видны границы, в которых разумно количественное описание, существование этих границ предостерегает от фетишизации чисел при математизации знания. Числа будут представлять "истинные" структуры только при определенном соотношении между преобразованиями, которые мы выбрали для сравнения состояний систем, и мономорфизмами категорий. Таким образом, сопоставить числа структурам (эксплицируемым категориями) можно всегда, но не обязательно эти числа будут упорядочены так же, как структуры. Заметим, что переход к инвариантам для анализа упорядочения структур является не обязательным, а лишь удобным методом, поскольку техника работы с числовыми структурами более разработана и привычна, нежели с произвольными. "Некардинализуемые" структуры, то есть те, упорядочение которых не согласуется с упорядочением кардинальных чисел, доступны, тем не менее, непосредственному исследованию категорными методами, но не подвластны технике анализа числовых инвариантов.

Из истории вариационных принципов

Мысль о том, что "природа действует простейшим образом" (И. Бернулли), т.е. "наиболее экономно", чрезвычайно стара и послужила источником многих научных идей и методических приемов. Сошлемся еще раз на И. Ньютона, который в своих "Началах" говорил, что не должно принимать в природе иных причин сверх тех, которые истинны и достаточны для объяснения явлений, что природа ничего не дает напрасно, а было бы напрасным совершать многим то, что может быть сделано меньшим, что природа проста и не роскошествует излишними причинами вещей. Эта мысль была источником не только методологии Ньютона, но и чисто физической идеи о равенстве тяжелой и инертной масс – идеи, имевшей столь далекие последствия в общей теории относительности.

Вскоре в математике и физике идея "экономии" в природе получила воплощение в развитии экстремальных принципов. Исторически первым таким принципом был "принцип Ферма" в геометрической оптике.

Еще Герон Александрийский выводил закон отражения света из принципа кратчайшего пути. Однако уже в случае преломления света этот принцип явно нарушался; поэтому П. Ферма предположил (1662 г.), что световой луч избирает не кратчайший путь, а путь наименьшего времени. Так был сформулирован первый экстремальный принцип, оставшийся незыблемым и по сей день: "Истинный путь светового луча отличается от всех возможных (мыслимых) путей тем, что время движения вдоль него минимально".

Вся геометрическая оптика заключена в этом принципе, как растение в зерне, и может быть получена из него путем методического развертывания с учетом конкретных условий движения света (плотность среды, наличие отражающих и преломляющих поверхностей и т.д.).

На этом примере можно видеть две основные черты, присущие всем экстремальным принципам: крайний лаконизм и простота и, в то же время, крайне общий и универсальный характер. Зная принцип Ферма, можно рассчитать любую оптическую систему, не нуждаясь ни в каких других законах геометрической оптики – все они являются лишь следствием этого принципа.

Итак, содержание всякого экстремального принципа является утверждение о минимуме (или максимуме) некоторой величины. Расчет траектории рассматривается как отыскание "истинного" пути среди всего множества возможных. Истинное движение отличается от всех возможных своей "оптимальностью", т.е. тем, что для него некоторая величина достигает минимума (или максимума). Таким образом, основная проблема состоит в том, чтобы найти минимизируемую величину, выяснить ее конструкцию. Не всегда это так просто сделать, как в оптике: механике пришлось ждать около ста лет, прежде чем соответствующая конструкция была найдена для нее.

15-го апреля 1744 года П. Мопертюи представил Парижской Академии мемуар, в котором предлагался новый универсальный принцип механики – принцип наименьшего действия: истинное движение отличается от всех возможных тем, что для него величина действия минимальна.

Само понятие действия – как произведения массы , скорости и пути – было введено еще Г. Лейбницем, причем ему, видимо, даже было известно, что в "истинных" движениях действие имеет всегда минимальное значение. Однако Лейбниц воздержался от формулировки какого-либо общего принципа, связанного с этим свойством действия. Мопертюи же провозгласил его наиболее общим законом природы. Законы движения и покоя, по мнению Мопертюи, выведенные из этого принципа, являются точно теми, которые наблюдаются в природе, и мы можем восхищаться результатами его применения ко всем явлениям: движение животных, произрастание растений, вращение светил является только его следствиями.

Мемуар вызвал среди ученых того времени ожесточенную полемику, далеко выходящую за рамки механики. Главным предметом спора было: являются ли события, происходящие в мире, причинно обусловленными или они телеологически направляются неким высшим разумом посредством "конечных причин", т.е. целей? Сам Мопертюи подчеркивал и отстаивал телеологический характер своего принципа и прямо утверждал, что "экономия действия" в природе доказывает существование бога.

Последний тезис вызвал резкий отпор со стороны материалистически настроенных ученых и публицистов того времени (Д´Аламбер, Дарси, Вольтер). Дискуссию вели и по другим направлениям, в частности, было подвергнуто критике определение действия, предложенное Мопертюи. Ряд авторов отрицал универсальный характер этого принципа, некоторые приводили примеры "истинных" движений, в которых "действие" не минимально, а наоборот, максимально. Велись споры и по вопросу о приоритете.

Л. Эйлер выступил в защиту приоритета Мопертюи, хотя сам сформулировал принцип наименьшего действия в более четкой и осторожной форме еще ранее него. Заслугой Мопретюи Эйлер считал универсальность его принципа; сам Эйлер рассматривал свой принцип лишь как средство решения некоторых задач механики.

Эйлер был первым, кто понял, что причинный и телеологический пути объяснения эквивалентны, хотя вначале он больше склонялся к телеологическим взглядам Мопертюи.

Окончательная формулировка принципа наименьшего действия, свободная от всякой "метафизики", принадлежит Ж. Лагранжу.

Лагранжа больше всего интересует формальная сторона механики и мало беспокоит физическое истолкование ее уравнений. В соответствии с этим он рассматривает минимизацию действия "не как метафизический принцип, а как простой и общий вывод из законов механики". Если Мопертюи и Эйлер рассматривали принцип наименьшего действия как первичный и основной закон механики, а все остальные законы – как его следствия, то после работ Лагранжа установилась позитивистская точка зрения, согласно которой экстремальные принципы суть только изящная и компактная упаковка для большого количества опытных фактов, не вносящая ничего нового в уже известные законы. Всякая попытка вернуть экстремальным принципам их прежнее положение – фундамента науки – клеймилась как теологическая. И только в ХХ веке революция, вызванная в физике теорией относительности и квантовой механикой, привела к пересмотру роли и места экстремальных принципов.

Выяснилось, что понятия и законы, лежащие в основании ньютоновской физики, не являются абсолютными: они изменяются при переходе от одной системы отсчета к другой. Действительно, основными законами природы могут считаться лишь те, которые остаются неизменными в любой системе отсчета. Оказалось, что этому требованию отвечают лишь экстремальные принципы. Можно считать, что в настоящее время этот спор решен окончательно: основные законы физики (а весьма вероятно, что и любой другой науки) должны иметь экстремальную форму (Полак, 1960)

Если стихийное развитие научной теории направлено к определенному идеалу, то ученый, очевидно, сэкономит себе силы и время, если уяснит себе форму этого идеала и будет стремиться к нему сознательно. Особенно успешным может оказаться такой подход в областях знания, которые еще не обрели строгой теоретической формы.

История действительно знает попытки такого рода. Открытие экстремальных принципов в свое время породило надежду, что к законам природы можно идти не только "снизу", путем индукции, обобщения фактов, но и "сверху", путем дедукции от экстремальных принципов. Эйлер, в частности, считал, что для этого только нужно путем общих "метафизических" рассуждений найти величину, которую "экономит" природа в данной области естествознания (т.е. "целевую функцию", "функционал"), и сформулировать соответствующий экстремальный принцип. В скрытом виде он содержит все нужные нам законы; получить их в явной форме – дело простой математической ловкости.

Несмотря на соблазнительную простоту этой программы, реализовать ее в то время не удалось ни самому Эйлеру, ни тем, кто пытался следовать за ним. Причина этого достаточно очевидна: не существовало никакого регулярного метода для отыскания экстремизируемой величины. Механике и оптике в этом смысле повезло: соответствующие величины были для них достаточно простыми и, в сущности, могли быть найдены путем перебора. Но уже в термодинамике максимизируемая величина – энтропия – не обладает ни простотой, ни достаточно очевидным физическим смыслом.

После ряда неудач программа Эйлера по отысканию законов природы "сверху" была заброшена. Более того, сами вариационные принципы были взяты под подозрение и урезаны в своих правах вследствие своего рода "телефобии", которой была заражена позитивистски настроенная наука XIX века.

Дифференциальные принципы

Спрашивается, не появились ли в наше время какие-нибудь новые предпосылки, позволяющие надеяться на успех реализации программы Эйлера?

На наш взгляд – появились. Прежде всего умножилось само число вариационных принципов, возникла возможность сравнивать, комбинировать и обобщать.

Далее, сложилось боле глубокое понимание некоторых идей, связанных с вариационными принципами: ("сила", "связь", "равновесие" и пр.). Стало, в частности, ясно, что специфические, сложные и разнообразные интегральные вариационные принципы механики могут быть получены как следствие более простых и общих дифференциальных принципов. А эти последние могут быть представлены в единообразной форме, выражающей идею равновесия системы (Кротов, 1967):

. (1)

Здесь – вектор обобщенной силы; – вектор возможных движений системы, совместимых с наложенными на нее связями.

Условие (1) означает ортогональность этих двух векторов: проекция силы на поверхность возможных движений системы равна нулю. Этим действительное (равновесное) состояние системы выделяется среди множества возможных. Иллюстрацией может служить известный в механике принцип возможных перемещений. Принцип позволяет найти равновесное состояние системы, которое – в случае его устойчивости – и совпадет с истинным состоянием.

В термодинамике условия равновесия, как их сформулировал Гиббс, являются другим примером вариационного принципа (1).

Очень часто силы могут быть получены как частные производные от некоторого потенциала по соответствующим координатам:

.

Тогда произведения могут рассматриваться как вариации этого потенциала, а сам принцип может быть записан в более компактной скалярной форме

Т.е. равновесное, истинное состояние системы определяется как точка стационарности потенциала.

В 1743 г. Д´Аламбер сформулировал принцип, позволивший распространить идею равновесия на динамику. К активным силам он добавил силы инерции . В этом случае истинное состояние (движение) системы выделяется из всего множества возможных тем, что для него вектор суммарной силы ортогонален любому вектору возможных перемещений :

(2)

Стоит подробнее остановиться на принципе Д´Аламбра, чтобы оценить ту важную идею, которую он вносит и которая может иметь далеко идущие последствия. Идея состоит в том, что понятие равновесия относительно. Нельзя говорить о равновесии, предварительно не указав тех факторов – сил и связей, которые уравновешиваются.

Система, неравновесная относительно одного набора факторов, может оказаться равновесной относительно другого.

Так атомное ядро неравновесно относительно кулоновских сил (протоны отталкиваются). Но может быть сделано равновесным за счет добавления ядерных сил. Живой организм неравновесен относительно термодинамических сил, но может быть сделан равновесным за счет добавления специальных управляющих сил.

Дело еще и в том, как определяется равновесие, что служит критерием равновесности или неравновесности. Чаще всего под равновесием по данной переменной понимают такое состояние, (значение ) в котором обращается в нуль скорость изменения . Но иногда под равновесием понимают обращение в нуль суммы сил, действующих на данную переменную. Последнее понимание является более общим. Оно включает в себя не только статистическое равновесие (когда скорость изменения переменной равна нулю), но и различные формы динамических равновесных ("стационарных") состояний. В таких состояниях ряд переменных может изменяться с постоянной скоростью. И даже падение с постоянным ускорение в поле тяжести может – в духе теории тяготения Эйнштейна – рассматриваться как движение в отсутствие сил, т.е. как равновесное.

В 1829 году Гаусс предложил еще один общий принцип механики, который он назвал принципом наименьшего принуждения:

(3)

Здесь – вектор возможных ускорений.

Наконец, в 1903 году Журден обнаружил существование третьего вариационного принципа механики:

(4)

где в качестве варьируемой переменной выступает скорость .

Сравнение трех принципов (2), (3), (4) показывает, что довольно безразлично, с помощью какой переменной – , или задается поверхность возможных движений, совместимых со связями, наложенными на систему. Тем не менее следует отметить, что принципы Журдена и Гаусса являются более общими, поскольку позволяют учитывать не только голономные ("позиционные"), ни и неголономные ("скоростные") связи. Однако вычислительные трудности, связанные с использованием этих принципов, привели к тому, что они не стали столь популярными, как принцип Д´Аламбера.

Привлекательность принципа Гаусса еще и в том, что в роли "потенциала" для него выступает простая квадратичная форма

которую Гаусс назвал принуждением. Сам принцип может быть записан в виде требования минимума этой квадратичной формы: .

Дьярмарти (1974) в поисках наиболее общей формы для вариационных принципов линейной неравновесной термодинамики пришел к принципу, который он также назвал принципом наименьшего принуждения – по аналогии с принципом Гаусса:

где – обобщенные термодинамические силы, – потоки, – сопротивления.

В этом случае, однако, возможна и более общая форма принципа, включающая помимо "диагональных" членов () также и смешанные члены ():

.

Такого рода квадратичные формы являются весьма типичными, поскольку любой потенциал вблизи точки экстремума может быть аппроксимирован такой формой. Это соответствует линейной аппроксимации зависимости между силами и координатами: . Можно надеяться, что именно такая форма принципа – хотя бы как аппроксимация – является универсальной, справедлива не только для механики или термодинамики, но и для других дисциплин.

Наиболее общая формулировка принципа наименьшего принуждения, не зависящая от природы системы, может быть получена так.

Пусть – равновесное, нормальное состояние системы; это состояние, в которое система переходит под действием внутренних сил ("реакций") когда внешние силы отсутствуют.

Будем предполагать, что реакция пропорциональна отклонению переменной от равновесия (нормы) и обратна по знаку этому отклонению , т.е. мы предполагаем, что система линейна и статически устойчива.

Пусть – внешняя сила, действующая на переменную ("приведенная" к этой переменной); в частном случае эта сила может быть и равной нулю.

Пусть, наконец, – действительное значение переменной, действительное состояние системы.

Тогда действительное состояние отличается от всего множества возможных тем, что принуждение для него минимально:

. (5)

Отсюда следует также дифференциальная форма принципа:

(значения , , фиксированы и варьирует только ).

В отсутствие внешних сил () принцип (5) принимает вид:

.

Действительное состояние определяется только связями между переменными .

Наконец, если и связи отсутствуют (переменные независимы), то действительное состояние совпадает с нормой , которая и является истинным, "наиболее равновесным" состоянием системы. Принуждение при этом обращается в нуль.

Итак, приступая к формулировке вариационного принципа для какой-нибудь новой области естествознания мы можем считать, что форма минимизируемой величины нам – в первом приближении – известна. Это квадратичная форма (5). Для ее полного определения нужно найти весовые коэффициенты . Как это можно было бы сделать? Здесь просматриваются два пути:

1) Прежде всего можно определить экспериментально. Если мы умеем измерять обобщенные силы и отклонения переменных от нормы , то весовой коэффициент определяется как отношение

.

Проблема в том, что чаще всего мы это делать не умеем. Механика и термодинамика являются счастливым исключением, но в других дисциплинах, как правило, методы измерения нужно создавать заново. При этом, помимо технических трудностей, возникают и непростые теоретические и методологические проблемы. В основном они связаны с понятием обобщенной силы, ее опрерациональным определением.

В механике и термодинамике обобщенные силы определяются через понятие энергии, как частные производные от некоторого потенциала по координатам. Но как определять обобщенные силы за пределами физики? Что делать, если нет понятия энергии или оно не играет определяющей роли в поведении системы? Выше мы определяли обобщенную силу (обобщенный) потенциал как частную производную от этого потенциала по соответствующей координате, т.е. как понятие вторичное. Но что делать, когда именно потенциал не известен и его нужно определить через силу, когда сила является первичным, исходным понятием?

Короче говоря, нужно независимое операциональное определение обобщенной силы.

2) Второй, более плодотворный, но и более трудный путь состоит в том, чтобы обратиться к "метафизическим" соображениям и попытаться понять, какая "истинная" минимизируемая величина скрывается за квадратичной аппроксимацией. При этом квадратичная форма служит всего лишь наводящим мостиком и особенно важно исследовать границы ее применимости, т.е. случаи, когда она перестает работать.

Проблема двойственности

Широкое обобщение понятия силы и соответствующего понятия координаты, возможность преобразования этих величин приводят к важному наблюдению, что во многих ситуациях они являются относительными или, как обычно говорят, "двойственными": сила может выступать в роли координаты, а координата – в роли силы. Глубокие основания этой двойственности лежат в относительности самих понятий причины и следствия: причина сама обычно является следствием какой-то другой причины, а следствие может стать причиной других следствий. Уже в механике мы видим, что активная сила является причиной изменения состояния (например, ускорения) системы, а изменение состояния в свою очередь служит причиной появления реакции системы (например, силы инерции). Еще более сложную взаимосвязь причин и следствий мы находим в процессах управления. Двойственность служит формальным выражением этой относительности.

Проблема двойственности наиболее полную разработку получила в теории оптимального управления (методы оптимизации, линейное и нелинейное программирование, математическая экономика (Гольдштейн, 1971)). Выглядит она следующим образом: пусть требуется найти максимум целевой функции

,

где – вектор, при наличии ограничений

,

Для решения задачи обычно используют метод множителей Лагранжа: строят функцию Лагранжа

и ищут ее максимум уже безо всяких ограничений. Переменные – множители Лагранжа. Эта задача называется прямой.

Однако множители Лагранжа изначально являются неопределенными. Поэтому возникает вторая задача – найти значения множителей Лагранжа, обеспечивающие максимум . Это и есть двойственная задача. В общем случае двойственные переменные – множители Лагранжа – также могут быть подвержены ограничениям. Такие ограничения должны быть согласованы с ограничениями на переменные .

Наиболее просто связь между условиями прямой и двойственной задачи выглядит в линейном программировании. Прямая задача: максимизировать целевую функцию при условиях . Двойственная задача: минимизировать целевую функцию при условиях . Здесь – векторы, – матрица. Одна из наиболее наглядных интерпретаций этих величин имеет место в экономике: – производимый продукт, – продажная цена единицы продукта, – получаемый доход, – ресурс, необходимый для производства продуктов, – стоимость единицы ресурса, – затраты на производство. Элементы матрицы – затраты -го ресурса на производство -го продукта (эта интерпретация с некоторой корректировкой терминов применима и в биологии).

Добавим, что ограничения в экономике обычно задаются в виде неравенств. Однако решение, как правило, лежит на границе допустимой области и в этом случае можно обойтись равенствами.

Доказан целый ряд теорем, касающихся свойств прямой и двойственной задачи и связей между ними. В частности показано, что если решение вообще существует, то оно совпадает в обеих задачах.

Существование двойственности обнаружено также в ряде областей физики, связанных с экстремальными принципами (механика, термодинамика и пр.). Массье в 1869 году первым обратил внимание на то, что в качестве независимых переменных, определяющих состояние системы, можно одинаково выбирать и энергию, и энтропию (Кричевский, 1970, с.219). Позднее (в 1875 году) Гиббс развил метод термодинамических потенциалов – "равноправных" функций состояния системы, которые одинаково хорошо можно использовать для описания и вывода уравнений системы, выбирая наиболее удобную функцию в зависимости от характера наложенных на систему ограничений (иначе говоря – независимых, извне задаваемых переменных). Например, вариационный принцип, устанавливающий критерий равновесия изолированной системы Гиббс формулирует следующим образом:

1) "Для равновесия любой изолированной системы необходимо и достаточно, чтобы при всех возможных изменениях состояния системы, не влияющих на ее энергию, вариация энтропии исчезала или была отрицательной": при .

2) "Для равновесия любой изолированной системы необходимо и достаточно, чтобы при всех возможных изменениях состояния системы, не влияющих на ее энтропию, вариация ее энергии исчезала или была положительной": при (цит. по Путилов,1971, с. 208).

В экологии сообществ предложено (Левич, Фурсова, 2002) обобщение теоремы Гиббса. Рассмотрена вариационная задача на условный экстремум (Левич,1982; Левич с соавт., 1994)

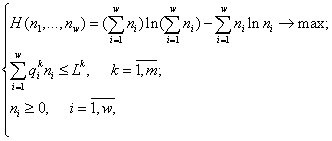(6)

где – искомые численности каждого из видов сообщества в стационарном состоянии, – количество -го ресурса, потребленное популяцией вида из среды в расчете на одну клетку к моменту остановки роста; – общее количество взаимонезаменимых ресурсов, потребляемых сообществом; – число видов в сообществе; – начальное содержание ресурса в среде .

Задача (6) является математической формализацией постулируемого экстремального принципа, согласно которому динамическая система из заданного состояния переходит в состояние с экстремальной (в пределах, допустимых имеющимися ресурсами) структурой (Левич,1982; Levich, 2000).

Приведем некоторые возможные интерпретации функционала и сформулированного экстремального принципа.

1. Энтропия может рассматриваться как мера "структурированности" некоторого состояния или мера "удаленности" структуры состояния от его бесструктурного аналога (Левич, 2001).

2. Энтропия, линейно упорядочивая сами структуры и описываемые математическими структурами состояния естественных систем, в определенном смысле в рамках функторного метода сравнения математических структур (Левич,1982) обобщает понятие "количество элементов" для конечных структурированных множеств (Левич, 2001). Тем самым, экстремальный принцип реализует максимум экспансии сообществ живых организмов (Levich, 2000).

3. Энтропию системы можно рассматривать как количество информации, связанной со структурой системы, поэтому введенный экстремальный принцип можно интерпретировать и в информационных терминах (Левич, 1978; Левич,1982).

4. Согласно обсуждаемой "теореме Гиббса" энтропийный экстремальный принцип с ограничениями по ресурсам равносилен принципу минимального потребления любого из лимитирующих динамику ресурсных факторов с ограничениями на наименьшую допустимую величину энтропийной характеристики системы.

5. Экстремальность функционала, порождающего динамику сообщества, можно интерпретировать и как требование максимального разнообразия системы, ограниченного доступными ресурсами среды (Левич,1980).

При исследовании сформулированной экстремальной задачи (6) при условии был получен ряд строгих результатов, среди которых следующие (Левич с соавт., 1994; Левич, Фурсова, 2002):

1. Максимум в задаче (6) достигается в точке, где ,

2. Теорема существования и единственности: для любого вектора ресурсов решение задачи (6) существует, единственно и задается формулой видовой структуры

(7)

где а общая численность и вектор есть решения системы алгебраических уравнений

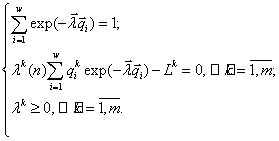
3. Теорема стратификации: все пространство ресурсов

является объединением непересекающихся подмножеств (стратов), находящихся во взаимно-однозначном соответствии с непустыми подмножествами множества в том смысле, что если некоторый вектор принадлежит подмножеству пространства ресурсов, соответствующему , то для этого вектора задача (6) эквивалентна задаче с равенствами

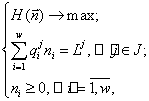
где

Заметим, что задача с неравенствами (6) сводится (редуцируется) к задачам с равенствами и в каждом страте решение задачи (7) зависит только от ресурсов (и потребностей в них), принадлежащих подмножеству . Причем именно эти ресурсы (и только они) потребляются полностью (являются лимитирующими), т.е. соответствующие неравенства из ограничений обращаются в равенства.

4. "Теорема Гиббса". Пусть мы имеем вектор соответствующий решению (7) задачи (6), и пусть Пусть данный вектор ресурсов принадлежит некоторому страту , причем для , для . Рассмотрим следующую экстремальную задачу:

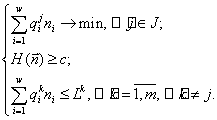(8)

Тогда решение (7) задачи (6) является одновременно решением системы (8). Верно и обратное утверждение: если вектор – решение системы (8), то вектор будет и решением задачи (6) с

Формализм Джейнса

Предложенный метод решения экологических, экономических и других задач с ограничениями по ресурсам представляет собой обобщение, так называемого, "формализма Джейнса", возникшего как обобщение известного физического принципа максимума энтропии, но получившего широкое распространение и за пределами физики.

В работах Джейнса (Janes, 1957) был предложен метод отыскания равновесных распределений вероятности при наличии дополнительных условий. В основе его лежит широкое обобщение принципа максимума энтропии и сочетание его с методом множителей Лагранжа.

Идея формализма является развитием известного "принципа недостаточного основания": если нам ничего не известно о величине , кроме того, что она лежит в некотором ограниченном диапазоне, то разумнее всего принять, что вероятности распределены в этом диапазоне равномерно. Потому что у нас нет доказательств, чтобы считать одно значение более вероятным, чем другое.

Но этот результат может быть получен также из принципа максимума энтропии, которая может рассматриваться как мера нашего незнания - и это самый честный и непредвзятый подход к определению вероятностей .

Однако этот подход может быть обобщен и на те случаи, когда нам что-то известно о величине , например, среднее значение некоторой функции от :

Для отыскания "самого непредвзятого" распределения в этом случае мы можем снова использовать требование максимизации энтропии

,

но на этот раз с учетом имеющейся у нас информации о среднем значении функции . Для учета дополнительных условий (их может быть несколько) используется метод множителей Лагранжа. С учетом условия нормировки, наложенной на вероятности

и дополнительных условий мы можем построить функцию Лагранжа:

Оптимальное (равновесное) распределение, отвечающее максимуму этой функции, имеет вид:

Множитель может быть найден из условия нормировки:

откуда

и выражение для может быть переписано:

Это обобщение распределения Больцмана на случай, когда имеется несколько ограничений (несколько "потенциалов" ).

Если в число координат входят и скорости, то мы получаем и распределение Гиббса (в этом случае - "кинетический потенциал"). Вообще все основные результаты равновесной термодинамики могут быть получены на основе такого подхода.

Следует отметить, что простой, изящный и универсальный формализм Джейнса до сих пор еще редко находит место в учебниках физики, хотя способен намного облегчить жизнь и студентам, и преподавателям. До сих пор для вывода статических распределений и вытекающих из них термодинамических функций используют громоздкие методы, восходящие еще к Гиббсу, сложные модели, не имеющие универсального значения. Чем это объяснить?

Одна из версий состоит в том, что принцип максимума энтропии в трактовке Джейнса (как меры незнания) имеет характер скорее логический, чем физический, говорит о субъективных свойствах нашего познания, а не об объективных законах природы. В определенном смысле он чужероден для физики – хотя, казалось бы, квантовая механика должны была приучить нас к мысли, что субъект и объект познания связаны теснее, чем казалось когда-то.

Как бы то ни было, но принцип максимума энтропии в трактовке Джейнса, постепенно завоевывает физику. (См., например, (Трайбус,1970; Хакен, 1971).

Однако наиболее успешное применение он нашел за пределами физики: в лингвистике (Мандельброт, 1973), математике (Gzil, 1995; Wu, 1997), экономике (Вильсон, 1978; Лихнерович, 1974; Розоноэр 1973), биологии (Термодинамика.., 1984), психологии (Голицын, Петров,1990), теории распознавания образов (Горохов с соавт., 1999), инженерной деятельности (Кудрин, 1993). Интересно, что в последние годы к принципу все чаще обращаются социологи, экономисты, лингвисты, инженеры и т.п.

Формализм Джейнса позволяет достаточно просто подойти и к отысканию равновесных состояний биологических сообществ при различных дополнительных условиях. Проблема эта имеет важные практические приложения, в частности, в экологии и постоянно привлекает внимание исследователей (см., например, работы А.К.Прица (1974), Ю.М.Свирежева и Д.О.Логофета (1978), Д.Лурье и Х.Вагенсберга (1984), А.П.Левича (1980; Levich, 2000), а также раздел по проблеме двойственности настоящего обзора).

Однако, основная проблема в применении этого принципа состоит в отсутствии явных процедур для сопоставления каждой из исследуемых систем адекватного ее природе энтропийного функционала. Даже в прародительнице энтропии - статистической физике - подходы к расчету энтропии в интересующих исследователя случаях крайне ограничены (как сетовал И.Пригожин, формулировка второго начала с точки зрения современного физика представляет собой скорее программу, чем утверждение, допускающее однозначную интерпретацию, так как ни Томпсон, ни Клаузис не указали точный рецепт, позволяющий выразить изменение энтропии через наблюдаемые величины). Поэтому обычная практика при работе с принципом максимума энтропии состоит в постулировании для исследуемой системы какого-либо аналога формул Больцмана или Шеннона. Наиболее последовательно указанная тенденция проявляет себя как раз в формализме Джейнса. Метод исследования систем Эдвина Томсона Джейнса состоит из нескольких рекомендаций:

1. Сопоставить допустимым состоянием системы определенные значения вероятности их реализации.

2. Сформулировать в виде неравенств ограничения на макропараметры системы (например, законы сохранения энергии, числа частиц и т.д.).

3. Отыскать равновесное состояние системы методом множителей Лагранжа как решения задачи на условный максимум с функционалом в форме шенновской энтропии.

Появившись в конце 60-х годов прошедшего века в статистической физике, формализм Джейнса прошествовал по многим областям знания, добавив к проблеме обоснования энтропийного функционала и проблему адекватного выбора ограничений на его экстремум, поскольку до решения вариационной задачи не известно, для каких макропараметров должны выполняться ограничения в виде строгих равенств, проблему, которая решена теоремой стратификации в подходе, обобщающем формализм Джейнса и представленным в предыдущем разделе.

Об экстремальных принципах биологии

Экстремальные принципы биологии находятся в стадии становления. Поэтому естественны и большое разнообразие этих принципов и не очень четкая, порой, их формулировка. Дело осложняется и тем, что живая материя организована в сложные иерархически системы: биосфера - биоценозы - популяции - особи - органы и ткани - клетки - органеллы - молекулы. И на каждом уровне организации могут существовать свои критерии оптимальности. Приложение принципа максимума энтропии к экологическим сообществам продемонстрировано в предыдущих разделах. Подробный обзор приложения экстремальных принципов в математической биологии опубликован недавно в работах с участием одного из авторов (Фурсова с соавт., 2003; Фурсова, Левич, 2002). В биологии вопрос о “целевой функции” стал более популярен с распространением эволюционного мышления в противовес статическому видению мира (Wilhelm, Brüggemann, 2000). Например, следующие экстремальные принципы: принцип минимума общего осмотического давления (Schuster, Heinrich, 1991); принцип максимальной общей скорости биохимической реакции (Wilhelm et al., 1994); принцип минимизации поверхностной энергии в развитии эмбриона (Goel, et al., 1986); принцип оптимальной конструкции (Розен, 1969); принцип максимума жизненного репродуктивного успеха особи (Терехин, 2001; Teriokhin, 1998); принцип максимальной биомассы потомства (Инсаров, 1975); принцип выживания (Ханин, 1982); принцип максимизации репродуктивных усилий (Zeide, 1991); принцип максимальной неожиданности протекания эволюции (Евдокимов, 1999). Известны вывод логистического уравнения роста популяции, основанный на требовании экстремальности функционала действия (Webb, 1995); применение принципа максимума Понтрягина в биоэкономической модели (Chaudhuri, 1986); принцип стационарного состояния открытых систем (Приц, 1974); принцип максимального разнообразия (Lurie et al., 1983); принцип максимума обобщенной энтропии (Левич, 1980; 1982; Levich, 2000; Левич с соавт, 1997; Shipley et al., 2006; Fursova, Levich, 2007); принцип минимума потребления лимитирующего вещества (Паников, 1991); принцип максимума мальтузианского параметра (Свирежев, 1991); принцип максимума использованной энергии (Печуркин, 1982); принцип максимального суммарного дыхания (Washida, 1995). Описаны экстремальные свойства сообщества с горизонтальной структурой (Свирежев, Логофет, 1978). В основе, так называемых, моделей динамической структуры лежит максимизация скорости изменения общего потока энергии через систему, асценденции, эмержентности, эксергии, косвенных эффектов, индекса зрелости (Jørgensen, Mejer, 1982; Jørgensen et al., 1995; Patten, 1986; 1995; Pérez-España, Arreguin-Sánchez, 1999). Использование термодинамики для решения проблем эволюции отражено в принципе наименьшей диссипации энергии и принципе наискорейшего спуска (Зотин А.И., Зотин А.А., 1999). Перечислим еще некоторые из экстремальных принципов: максимальное рассеяние энергии (Ulanowicz, Hannon, 1987; Schneider, Kay, 1994; Mauersberger, 1996) , максимизация биомассы (Margalef, 1968), максимум устойчивости органического вещества (Whittaker, Woodwell, 1971).

Обратим внимание на то, что для биологических систем чрезвычайно типичны и важны такие процессы как потеря устойчивости, уход от равновесия и переход к новому равновесию. Такие процессы мы наблюдаем на всех уровнях организации - от клеток и молекул до биоценозов и биосферы в целом. Развитие индивида, поведение, творчество, эволюция биосферы - основаны именно на таких неустойчивых процессах. Желательно было бы найти экстремальный принцип, который, с одной стороны, адекватно описывал бы динамику этих процессов, а с другой - сохранял бы преемственность по отношению к известным экстремальным принципам, включая их в себя как предельные частные случаи.

Одна из наиболее интересных попыток такого рода принадлежит Эйгену (Эйген, Шустер, 1982). Составленное им эволюционное уравнение описывает эволюцию некоего сообщества видов. (Последние могут трактоваться очень широко, так что уравнение пригодно, например, для описания процессов восприятия). Вообще говоря, подобное уравнение или его общий аналог могут быть получены как следствие некоторого экстремального принципа. Что это может быть за принцип?

Нам кажется, что в поисках такого принципа нужно исходить из центральной аксиомы биологии: живой организм формируется в процессе адаптации к условиям окружающей среды. Адаптированность, приспособленность является условием выживания в этой среде и определяет все реакции и свойства организма. Формальное описание этого факта могло бы послужить отправной точкой поиска.

В ряде работ (см., например, Голицын, Петров, 1990; 1991; 2005; Голицын, 1997) было выдвинуто предположение, что наиболее общей и адекватной мерой адаптации системы к окружению является средняя взаимная информация между условиями среды и признаками или реакциями системы . А основным принципом, определяющим поведение и развитие системы, является принцип максимума информации:

(9) Здесь - условная и безусловная энтропия, - условная и безусловная вероятность.

В своих работах по теории информации А.Н.Колмогоров показал (Колмогоров, 1987), что под величинами не обязательно понимать вероятности, это могут быть просто относительные доли, части, концентрации. Подход Колмогорова, сохраняя основной математический аппарат теории информации, в то же время резко расширяет сферу применимости.

Принцип максимума информации означает, что по мере адаптации к среде признаки и реакции организма со все большей полнотой и точностью отражают условия среды. У хорошо приспособленного организма эта взаимная информация так велика, что биолог, наблюдая признаки организма, может довольно точно описать условия среды, в которой тот обитает. И наоборот, зная условия среды, можно довольно правильно предсказать признаки организма, способного выжить в этой среде.

Заметим, что принцип максимума информации включает в себя и принцип максимума энтропии при фиксированном .

Из этого принципа следует также эволюционное уравнение, сходное с уравнением Эйгена, но в некоторых отношениях более общее:

(10)

Здесь - информативность признака в условиях ; - средняя информативность; - относительная доля ("вероятность") комбинации .

Из приведенного уравнения видно, что в отличие от уравнения Эйгена, информативность, характеризующая селективное преимущество признака, зависит от условий среды . Поэтому не только изменение признака (мутация), но и изменение условий среды может изменить информативность и дать толчок новому направлению эволюции. Система эволюционирует вместе с окружающей средой - это, конечно, более реалистическая точка зрения; и примеров, когда равновесие нарушалось именно изменением условий среды, давая преимущество одним видам и уничтожая другие, - можно найти огромное количество.

Система уравнений (10) задает некоторое преобразование начального состояния (вектора вероятностей) системы в конечное, равновесное. Число таких возможных равновесных состояний определено числом собственных векторов линеаризованного преобразования. Неустойчивость процесса проявляется в том, что ничтожное изменение начальных условий может совершенно изменить ход эволюции и привести систему к другому "аттрактору" (равновесному состоянию). Таким образом, принцип максимума информации и эволюционное уравнение (14) описывают не только устойчивый процесс выбора вблизи равновесного состояния, но и бифуркации эволюционного процесса. Принцип максимума взаимной информации является более общим, чем принцип минимума различающей информации и переходит в последний только вблизи равновесия. Покажем это более подробно.

Пусть система достигла одного из равновесных состояний, характеризуемых распределением вероятностей . Взаимная информация между и в этом состоянии может быть разбита на две части следующим образом:

Здесь - состояние, близкое к равновесному /возникшее, например, вследствие како-то флуктуации/; - различающая способность между и ; - взаимная информация, усредненная по . Поскольку вблизи равновесия , то приближенно можем заменить эту величину на среднюю взаимную информацию между и , т.е. на . Поскольку постоянна и не варьируется, то и выражение в целом постоянно. Поэтому требование максимизации взаимной информации равносильно требованию минимума различающей информации , т.е. вблизи равновесного состояния принцип максимума взаимной информации переходит в принцип минимума различающей информации. Но – только вблизи равновесия. Вообще же принцип максимума информации является более общим и адекватно описывает также процессы вдали от равновесия.

Более подробное обсуждение и некоторые дополнительные аргументы в пользу принципа максимума взаимной информации можно найти в работах Г.А.Голицына и В.М.Петрова (1990; 1991; 1997; 2005).

Почему выполняется экстремальный принцип для энтропии?

Почему же в мире действуют экстремальные принципы? Готфрид Вильгельм Лейбниц считал – потому, что мы с вами живем в "лучшем из миров". Необходимо додумать эту мысль – в чем конкретно наш мир так хорош, что в нем действуют экстремальные принципы. Нами движет не только любопытство, но и потребность науки в поиске законов изменчивости мира, особенно в тех исследовательских областях, для которых гениальное угадывание фундаментальных уравнений еще не свершилось.

И уравнения движения, и экстремальные принципы – это инструменты теоретического естествознания. Единственный путь построения формальной теории, открытый для теоретика, состоит в подборе математической структуры, удачно описывающей интересующий исследователя фрагмент реальности.

Да и сама математика, по словам многоголового автора эпохи Н.Бурбаки (1963), представляет собой переплетение нескольких математических структур – алгебраической, топологической и структуры порядка. Для описания произвольных математических структур, как уже было сказано, удобен язык математической теории категорий и функторов. Две особенности теоретико-категорного описания систем позволяют думать, что язык теории категорий более адекватен для описания реальности, нежели язык математики, основанной на теории множеств. Первая особенность – возможность оперировать сразу всей совокупностью одинаково структурированных множеств, что позволяет отождествить эту совокупность с пространством всех возможных состояний системы. Вторая особенность – та, что в категорию наряду со структурированными объектами равноправно и обязательно входят все допустимые их структурой способы изменения объектов, или преобразования состояний системы. Это позволяет заменить теоретико-множественное идеализированное представление мира в виде "застывших" объектов на адекватное миру представление его процессами.

Поиск выделенных – реально осуществляющихся – состояний систем среди всех потенциально возможных в методологии экстремальных принципов требует, во-первых, умения каким-либо образом упорядочить состояния между собой на шкале "больше-меньше", "сильнее-слабее" и т.п. и, во-вторых – выбора экстремального из этих состояний в полученном упорядочении. На языке математических структур такой поиск означает умение упорядочить структурированные множества, описывающие систему, и выбрать наиболее "сильную" (или наиболее "слабую") структуру в качестве той, что выделяет "реальное" состояние из всех возможных. Назовем сформулированное утверждение "принципом экстремальной структуры".

Теория категорий и функторов представляет аппарат, позволяющий сравнивать по "силе структур" любые структурированные множества. Метод сравнения легче всего понять, рассмотрев предельный случай структурированных множеств – множества без структуры. Для сравнения таких множеств можно использовать такую характеристику, как количество элементов в них (синонимы – кардинальные числа множеств, мощности множеств). Любые два множества сравнимы по количеству элементов. Для множеств со структурой характеристика по количеству элементов неинформативна, поскольку никак не связана со структурой. Однако, само понятие количества элементов не первично, а возникает как математическая конструкция при сравнении множеств с помощью соответствий между ними. Термины "изменение объектов", "преобразование состояний", упомянутые в предыдущих абзацах, в данном контексте можно считать синонимами термина "соответствие". Частный случай соответствий представляют собой привычные функции, или отображения. Поясним примером метод сравнения множеств с помощью соответствий. Зададимся вопросом: чего (или кого) больше в некой комнате – стульев или людей? Один из способов ответить на этот вопрос – подсчитать количества стульев и людей, а затем сравнить полученные числа. Другой способ – установить соответствие между людьми и стульями, например, попросив, чтобы каждый из присутствующих в комнате людей занял один стул. После того, как люди рассядутся, мы сможем точно ответить больше ли в комнате стульев или людей в зависимости от того, остались ли свободными стулья или – стоящими без сидячего места люди. Замечу, что при этом мы можем не знать ни количества стульев, ни количества людей в комнате. Повторю, что процедура сравнения множеств с помощью соответствий носит более общий характер, чем подсчет количества элементов множеств.

Применение сравнения структурированных множеств с помощью преобразований (соответствий), сохраняющих имеющуюся структуру, порождает "структурные числа" структурированных множеств, обобщающие понятия кардинального числа, или "количества элементов", используемые для множеств без структуры (структурные числа превращаются в обычные количества элементов для частного случая бесструктурных множеств). Однако, структурные числа – это не конечная остановка на нашем пути к методу поиска экстремальных структур. Дело в том, что в отличие от бесструктурных множеств, которые всегда сравнимы с помощью числа элементов в них, структурированные множества могут оказаться не сравнимыми между собой, поскольку необходимые для сравнения соответствия могут существовать не для любой пары структурированных множеств. Это значит, что траектория "движения" системы от одного состояния к другому – "более сильному" – состоянию может прерваться из-за невозможности сравнить состояния, чтобы применить экстремальный принцип.

В математике существует способ обойти создавшуюся трудность с помощью метода "представлений". Метод состоит в замене объектов и преобразований одной категории объектами и преобразованиями другой. Делается это так, чтобы задаваемые структурой первой категории связи между объектами и между их преобразованиями не были нарушены. Вне математики подобный метод называют "методом аналогий". Собственно, представления из одной категории в другую и названы функторами, фигурирующими в названии теории наравне с категориями. Для любой категории структурированных множеств существует особый функтор в категорию множеств без структуры. Этот функтор сопоставляет каждому структурированному множеству совокупность его допустимых структурой преобразований. Оказывается, что количества этих преобразований упорядочены так же, как структурные числа множеств (если структурные числа сравнимы). Доказательство этой теоремы, а также строгие формулировки приводимых здесь утверждений содержатся в работе, специально посвященной применению теории категорий и функторов для описания систем (Левич, 1982). Предложенный метод сравнения структурированных множеств назван "функторным сравнением структур", а количество допустимых преобразований структурированных множеств – их "функторными инвариантами", или "функторными числами". Замечу, что функторные числа представляют собой следующее за структурными числами обобщение понятия "количества элементов" (Левич, 2001). Согласно этому обобщению, "правильное" сравнение структурированных множеств состоит в сравнении количеств их преобразований, не нарушающих заданную на множествах структуру. Для методологии применения экстремальных принципов оказывается очень важным, что функторные числа в отличие от структурных чисел сравнимы для любых структурированных множеств, т.е. экстремальный принцип, сформулированный на языке функторных чисел, применим для сравнения любых состояний исследуемой системы.

Уже проведенные и дальнейшие рассуждения должны продемонстрировать путь по созданию метода расчета (а не угадывания) экстремизируемых функций при применении методологии экстремальных принципов. На этом пути нам необходимо сделать следующий шаг. Количество допустимых структурой системы преобразований зависит от двух характеристик структурированного множества: от количества элементов в нем и от заданной на множестве структуры. Если мы хотим, чтобы экстремизируемая функция отражала именно свойства структуры, то вместо количества допустимых преобразований необходимо использовать удельное их количество (т.е. количество, приходящееся на один элемент множества). Можно показать, что удельные функторные инварианты упорядочены так же, как сами функторные инварианты, т.е. задачу о поиске экстремальных состояний систем они способны решать так же, как предшествующее обобщение чисел.

Полученная конструкция удельного инварианта структуры системы известна в науке под несколько другим именем. Чтобы понять это, назовем сохраняющуюся при допустимых преобразованиях структуру состояния системы его "макросостоянием", а состояния, в которые данное состояние переходит при допустимых преобразованиях – его "микросостояниями". Поскольку число состояний, в которые переходит данное состояние при допустимых преобразованиях, в точности равно числу этих преобразований, то в новых терминах удельный инвариант оказывается удельным количеством микросостояний, соответствующих заданному макросостоянию системы. Позволим теперь себе взять логарифм (по основанию, большему единицы, чтобы упорядочение прологарифмированных величин не изменилось на противоположное) от этого числа микросостояний. (Можно полагать операцию по взятию логарифма данью традиции, а можно обратиться к обоснованию этой процедуры (Левич, 2004). В полученной конструкции опытный читатель сразу узнает ремейк больцмановского определения энтропии. Поэтому назовем логарифм удельного числа допустимых преобразований данного состояния системы его "обобщенной энтропией". Все сказанное выше позволяет считать обобщенную энтропию, во-первых, мерой структурированности состояний системы (можно уточнить – мерой удаленности состояния от его бесструктурного аналога, энтропия которого равна нулю) и, во-вторых, функцией состояния, непосредственно связанной с обобщением понятия о количестве элементов для структурированных множеств. Замечу, что возникшая конструкция энтропии получена вне каких-либо статистических или вероятностных предпосылок. Величина обобщенной энтропии может быть строго рассчитана для состояний любых систем, эксплицируемых математическими структурами. Она может быть вычислена для состояний, описываемых множествами с любым – большим или малым – количеством элементов. Вероятностные интерпретации могут возникать при рассмотрении определенных типов систем, но они совершенно не обязательны для расчетов энтропии. Для некоторых математических структур, например, для множеств с разбиениями, формула для обобщенной энтропии полностью совпадает с формулами для энтропии идеального газа Л.Больцмана или для энтропии каналов связи К.Шеннона. Функторные инварианты многих (а, возможно, и всех) математических структур могут быть выражены через инварианты ассоциированных со структурами разбиений. Возможно, этот математический факт объясняет "вездесущность" появления энтропии при описании самых различных естественных и антропных систем. А упомянутая выше связь конструкции энтропии с обобщением понятия "количество элементов" может служить методическим обоснованием методологического принципа, согласно которому "числа правят миром".

В рамках поставленной перед собой задачи по поиску экстремального принципа проследим цепочку возникших у нас в ходе исследования формулировок:

1. Следует отыскивать экстремальное состояние системы.

2. Для системы, моделируемой структурированными множествами, следует отыскивать состояние с экстремальной (например, с наиболее "сильной") структурой.

3. Следует отыскивать состояние системы, обладающее наибольшим (удельным) функторным инвариантом, т.е. наибольшим (удельным) количеством допустимых структурой системы преобразований.

4. Следует отыскивать состояние, обобщенная энтропия которого максимальна.

Осталось сделать заключительный шаг на пути формулирования искомого экстремального принципа. Этот шаг не следует из предшествующих построений, а связан с таким свойством изменяющихся систем, как открытость по отношению к потребляемым ресурсам. Мы исходим из исследовательской установки, утверждающей, что любые изменяющиеся системы потребляют некоторый ресурс. Это очевидно для систем, открытых по отношению к энергии или веществу, менее очевидно для закрытых систем, например, если изменение представляет собой механическое движение закрытой системы. Ресурсом, "потребляемым" такой движущейся системой, можно считать необходимое для движения пространство (Левич, 1996). Впрочем, несогласный с такой установкой читатель может полагать, что рассмотрен лишь класс открытых в его понимании систем.

Еще одна принимаемая мною предпосылка утверждает, что допустимые изменения системы всегда ограничены нехваткой каких-либо ресурсов. Из-за этого в экстремальном принципе, порождающем закон изменчивости, экстремум обязательно должен быть условным.

В силу сказанного искомый принцип может звучать следующим образом: из заданного состояния система переходит в такое состояние, для которого обобщенная энтропия максимальна в пределах, задаваемых доступными системе ресурсами. Упоминание об ограничениях ресурсами – основное отличие приведенного принципа от Второго начала термодинамики (действующего исключительно в закрытых системах). Безусловный максимум энтропии, требуемый Вторым началом, приводит к однородному распределению характеристик системы, называемому "тепловой смертью". Условный экстремум энтропии для открытых, но ограниченных по ресурсам систем влечет неоднородные распределения. Причем степень их неоднородности может быть сколь угодно велика в зависимости от различий компонентов исследуемой системы по потребностям в ресурсах, ограничивающих развитие (Левич, 1980).

Соответствующая формулировка экстремального принципа звучит так: из заданного состояния система переходит в такое состояние, для которого потребление ограничивающих рост ресурсов минимально в пределах, задаваемых необходимой степенью структурированности системы.

Заключение

В заключение можно сказать, что обобщенный принцип равновесия в форме (1), принцип наименьшего принуждение (5) и его статистический аналог – принцип максимума различающей информации (9) – уже сейчас могут служить надежной базой для отыскания экстремальных принципов в самых разных областях естественных и гуманитарных наук.

Резюмируем другие продемонстрированные результаты:

Природные и антропные системы моделируются математическими структурами.

На языке математической теории категорий и функторов система – это класс одинаково структурированных множеств, или макросостояние системы плюс класс допустимых преобразований этих множеств, или ее микросостояния.

Состояния системы можно упорядочить по числу допустимых ими преобразований. Этот способ упорядочения обобщает понятия "количество элементов" для бесструктурных множеств и "сила структур" для структурированных множеств.

Обобщенная энтропия состояния системы может быть определена через логарифм количества допустимых состояний преобразований и, в свою очередь, интерпретирована как мера структурированности состояния (мера удаленности состояния от его бесструктурного аналога) или как мера "обобщенной числовой мощности" состояния.

Для отыскания законов изменчивости систем может быть предложен обобщенный формализм, основанный на принципе максимума обобщенной энтропии.

Принцип максимума эквивалентен:

· принципу реализации экстремального состояния системы;

· принципу реализации максимальной структуры ("сложности", "разнообразия", "структурной информации" и.т.п.);

· принципу максимальной (обобщенной) экспансии системы, т.е. ее "количественному" росту;

· принципу наименьшего "потребления" ограничивающих ресурсов или их определенной комбинации, которую можно назвать "обобщенной свободной энергией" системы;

Приложения рассмотренных в статье принципов в гуманитарной области (поведение, творчество, искусствознание, культура, эмоции…) подробно продемонстрированы в работах Г.А.Голицына и В.М.Петрова (1990; 1991; 1997; 2004; 2005).

Литература

Акчурин И.А. Единство естественно-научного знания. М.: Наука, 1974, С. 108-114.

Бирюков Б.В. Кибернетика и методология науки. М.: Наука, 1974. С.247.

Букур И., Деляну А. Введение в теорию категорий и функторов. М.: Мир, 1972. С. 93-96.

Бурбаки Н. Алгебра. Алгебраические структуры. М.: ГИФМЛ, 1962. С. 88.

Бурбаки Н. Архитектура математики // Очерки по истории математики. М.: Мир, 1963. С. 245-259.

Бурбаки Н. Теория множеств. М.: Мир, 1965. С. 396-397.

Виленкин Н.Я, Шрейдер Ю.А. Мажоритарные пространства и квантор "большинства" // Семиотика и информатика. 1976. № 8. С. 45-82.

Вильсон А.Дж. Энтропийные методы моделирования сложных систем. М.: Мир, 1978. 248 с.

Голицын Г.А. Информация и творчество. М.: Русский мир, 1997. 304 с.

Голицын Г.А., Петров В.М. Гармония и алгебра живого. М.: Знание, 1990. 128 с.; 2-е издание. М.: КомКнига, 2005.

Голицын Г.А., Петров В.М. Информации – поведение – творчество. М.: Наука, 1991. 224 с.

Голицын Г.А., Петров В.М. Социальная и культурная динамика: долговременные тенденции (информационный подход). М.: КомКнига, 2005. 272 с.

Гольдштейн Е.Г. Теория двойственности в математическом программировании и ее приложения. М.: Наука, 1971.

Горохов В.Л., Витковский В.В., Бузников А.А. Термодинамические и информационные процессы в космическом мониторинге. С-Пб.: ЛЭТИ, 1999.

Евдокимов Е.В. Проблемы регулярного поведения и детерминированного хаоса в основных моделях популяционной динамики (теория и эксперимент). Автореферат диссертации на соискание ученой степени доктора биологических наук. Красноярск, 1999. 40 с.

Зотин А.И., Зотин А.А. Направление, скорость и механизмы прогрессивной эволюции: Термодинамические и экспериментальные основы. М.: Наука, 1999. 320 с.

Инсаров Г.Э. Ступенчатая модель роста и размножения организмов // Количественные аспекты роста организмов. М.: Наука, 1975. С.114.

Колмогоров А.Н. К логическим основам теории информации и теории вероятностей // Проблемы передачи информации. Вып. 1. М.: 1965.

Колмогоров А.Н. Три подхода к определению "количества информации" // Колмогоров А.Н. Теория информации и теория алгоритмов. М.: Наука, 1987. 304 с.

Кричевский И.Р. Понятия и основы термодинамики. М.: Химия, 1970. 440 с.

Кротов В.Ф. Законы состояния в математическом естествознании // Оптимальные системы автоматического управления. М.: Наука, 1967. С. 163-219.

Кудрин Б.И. Введение в технетику. Томск: Изд-во Томского университета, 1993.

Левич А.П. Информация как структура систем // Семиотика и информатика. 1978. №10. С. 116-132.

Левич А.П. Структура экологических сообществ. М.: Изд-во Моск. ун-та, 1980. 181 с.

Левич А.П. Теория множеств, язык теории категорий и их применение в теоретической биологии. М.: Изд-во Моск. университета, 1982. 190с.

Левич А.П. Семиотические структуры в экологии, или существует ли экологический код? // Человек и биосфера. М.: Изд-во Моск. университета, 1983. С. 68-77.

Левич А.П. Время как изменчивость естественных систем: способы количественного описания изменений и порождение изменений субстанциональными потоками // Конструкции времени в естествознании: на пути к пониманию феномена времени. Часть 1. Междисциплинарное исследование. М.: Изд-во Моск. университета, 1996. С. 149-192.

Левич А.П. Энтропия как обобщение понятия количества элементов для конечных множеств // Философские исследования. 2001. №1. С. 59-72.

Левич. А.П. Почему выполняются экстремальные принципы для энтропии и времени? // Пространство и время: физическое, психологическое, мифологическое. М.: КЦ "Новый Акрополь", 2004. С. 87-94.

Левич А.П., Алексеев В.Л., Никулин В.А. Математические аспекты вариационного моделирования в экологии сообществ // Математическое моделирование. 1994. Т.6. №5. С.55-76.

Левич А.П., Максимов В.Н., Булгаков Н.Г. Теоретическая и экспериментальная экология фитопланктона. М.: Изд-во НИЛ. 1997. 192 с.

Левич А.П., Фурсова П.В. Задачи и теоремы вариационного моделирования в экологии сообществ // Фундаментальная и прикладная математика. 2002. Т. 8. № 4. С. 1035-1045.

Лихнерович М. Модель экономического обмена (экономика и термодинамика) // Математическая экономика. М.: Мир, 1974. С. 101-142.

Лурье Д., Вагенсберг Х. Экстремальный принцип для разнообразия биомассы в экологии // Термодинамика и регуляция биологических процессов. М.: Наука, 1984. С. 153-163.

Мазур М. Качественная теория информации. М.: Мир, 1974. С.70.

Мандельброт Б. Теория информации и психолингвистика: теория частот слов // Математические методы в социальных науках. М.: Прогресс, 1973.

Паников Н.С. Кинетика роста микроорганизмов. Общие закономерности и экологические приложения. М.: Наука, 1991. 309 c.

Петров В.М. Количественные методы в искусствознании. М.: Академический проект, 2004.

Печуркин Н.С. Энергетические аспекты развития надорганизменных систем. Новосибирск: Наука, 1982. 112 c.

Полак Л.С. Вариационные принципы механики, их развитие и применение в физике. М.: Физматгиз, 1960. 600 с.

Приц А.К. Принцип стационарных состояний открытых систем и динамика популяций. Калининград: Балт. НИРО, 1974. 123 с.

Путилов К.А. Термодинамика. М.: Наука, 1971. 376 с.

Розен Р. Принцип оптимальности в биологии. М.: Мир, 1969. 215 c.

Розоноэр. Л.И. Обмен и распределение ресурсов (обобщенный термодинамический подход), I-III // Автоматика и телемеханика, 1973. №№5, 6, 8.

Свирежев Ю.М. Феноменологическая термодинамика взаимодействующих популяций // Журн. общ. биологии. 1991. Т. 52. № 6. С. 840.

Свирежев Ю.М., Логофет Д.О. Устойчивость биологических сообществ. М.: Наука, 1978. 352 с.

Терехин А.Т. Оптимизационное моделирование эволюции жизненного цикла. Автореферат диссертации на соискание ученой степени доктора биологических наук. Москва. 2001. 53 c.

Термодинамика и регуляция биологических процессов. М.: Наука, 1984.

Трайбус М. Термостатика и термодинамика. М.: Энергия, 1970. 502 с.

Фурсова П.В., Левич А.П. Математическое моделирование в экологии сообществ. Обзор литературы // Проблемы окружающей среды и природных ресурсов. 2002. №9. М.: ВИНИТИ. 98 с.

Фурсова П.В., Левич А.П., Алексеев В.Л. Экстремальные принципы в математической биологии // Успехи современной биологии. 2003. Т.123. №2. С.115-137.

Хакен Г. Информация и самоорганизация. М.: Мир, 1971. 240 с.

Ханин М.А. Энергетика и критерии оптимальности онтогенетических процессов // Математическая биология развития. М.: Наука, 1982. С. 177.

Цаленко М.Ш., Шульгейфер Е.Г. Основы теории категории. М.: Наука, 1974. С. 15-17.

Шаров А.А. Понятие информации в теории категорий // Семиотика и информатика. 1976. №8. С. 166-178.

Шеннон К. Работы по теории информации и кибернетике. М.: Мир, 1963. С. 143-332.

Шрейдер Ю.А. О семантических аспектах теории информации // Информация и кибернетика. М.: Советское радио, 1967. С. 15-47.

Шрейдер Ю.А. К построению языка описания систем // Системные исследования. Ежегодник. М: Наука, 1973. С. 226–238.

Шрейдер Ю.А. Информация и метаинформация // НТИ. Сер. 2. 1974. № 4. С. 3-10.

Эйген М., Шустер П. Гиперцикл. Принципы самоорганизации макромолекул. М.: Мир, 1982. 270 с.

Blanchard A. Structure species and constructive functors // Canad J. Math. 1974. 26. № 5. Р. 1217–1227.

Cerny J., Brunovsky P. A note on information without probability // Inform. and Contr. 1974. 25. №2. P. 134-144.

Chaudhuri K. A bioeconomic model of harvesting a multispecies fishery // Ecological Modelling. 1986. V. 32. P. 267.

Fursova P.V., Levich A.P. Variational model of microorganism polyculture development without re-supply of mutually irreplaceable resources // Ecological Modelling. 2007. V. 200. № 1-2. P. 160-170.

Goel N.S., Doggenweiler C.F. and Thompson R.L. Simulation of cellular compaction and internalization in mammalian embryo development as driven by minimization of free energy. // Bull. Math. Biol. 1986. V. 48. № 2. P. 167.

Gzil M. The method of maximum Entropy. Singapore, New Jersey, London, Hong Kong: World Scientific. 1995.

Ingarten R.S., Urbanik К. Information without probability // Coll. Math. 1962. 9. № 1. P. 15-20.

Janes E.T. Information theory and statistical mechanics // I. Phys. Rev. 1957. V.106. №4. Pp. 620-630. II. Phys. Rev. 1957. V.108. №2. Pp. 171-190.

Jørgensen S.E., Mejer H. Next generation of ecological models // Proceedings of the Work Conf. on Envir. Syst. Anal. and Manag. Rome, 1982. P. 485.

Jørgensen S.E., Nielsen S.N., Mejer H. Emergy, environ, exergy and ecological modelling // Ecological modelling. 1995. V. 77. P. 99.

Levich A.P. Variational theorems and algocoenoses functioning princeples // Ecological Modelling. 2000. V.131. № 2-3. Pp. 207-227.

Lurie D., Valls J., Wagensberg J. Thermodynamic approach to biomass distribution in ecological systems // Bull. Math. Biol. 1983. V. 45. P. 869.

Margalef R. Perspectives in ecological theory. Chicago: Chicago University Press, 1968. 122 p.

Mauersberger P. From a theory of local processes in aquatic ecosystems to a theory at the ecosystem scale // Sci. Total Environ. 1996. V. 183. P. 99.

Patten B.C. Energy cycling, length of food chains, and direct versus indirect effects in ecosystems // Ecosystem Theory for Biological Oceanography. Can. Bull. Fish. Aquat. Sci. 1986. V. 213. P. 119.

Patten B.C. Network integration of ecological extremal principles: exergy, emergy, power, ascendency and inderect effects // Ecological modelling. 1995. V. 79. P. 75.

Pérez-España H., Arreguin-Sánchez F. A measure of ecosystem maturity // Ecologocal Modelling. 1999. V. 119. P. 79.

Rashewski N. Life, Information Theory and Topology // Bull Math. Bioph. 1955. V. 17. № 3.

Schneider E.D., Kay J.J. Life as a manifestation of the second law of thermodynamics // Math. Comput. Model. 1994. V. 19. P. 25.

Schuster S., Heinrich R. Minimization of intermediate concentrations as a suggested optimality principle for biochemical networks I. Theoretical analysis. // J. Math. Biol. 1991. V. 29. P. 425.

Shipley B., Vile D., Garnier E. From Plant Traits to Plant Communities: A Statistical Mechanistic Approach to Boidiversity // Science. V. 314. November 2006. P. 812-814.

Teriokhin A.T. Evolutionarily optimal age schedule of repair: Computer modelling of energy partition between current and future survival and reproduction // Evolutionary Ecology. 1998. V. 12. P. 291.

Ulanowicz R.E., Hannon B.M. Life and production of entropy // Proc. R. Soc. Lond, 1987. V. 232. P. 181.

Urbanik K. On the concept of information // Progr. Statist. 2. Amsterdam-London. 1974. P. 863-868.

Washida T. Ecosystem configurations consequent on the maximum respiration hypothesis // Ecoligical Modelling. 1995. V. 78. P. 173

Webb J.N. Hamilton’s variational principle and ecological models // Ecoligical Modelling. 1995. V. 80. P. 35.

Whittaker R.H., Woodwell G.M. Evolution of natural communities // Ecosystem Structure and Function. Corvallis: Oregon State University Press, 1971. P. 137.

Wilhelm T., Brüggemann R. Goal functions for the development of natural systems // Ecological Modelling. 2000. V. 132. P. 231.

Wilhelm T., Hoffmann-Klipp E., and Heinrich R. An evolutionary approach to enzyme kinetics: optimization of ordered mechanisms // Bull. Math. Biol. 1994. V. 56. № 1. P. 65.

Wu N. The Maximum Entropy Method. Springer. 1997.

Zeide B. Quality as a characteristic of ecological models // Ecological Modelling. 1991. V. 55. № 3–4. P. 161.

Контактные координаты:

Александр Петрович Левич, д.б.н., в.н.с. кафедры общей экологии Биологического факультета МГУ им. Ломоносова

Тел. служ.: 939-5560

E-mail: apl@chronos.msu.ru

---

* Работа поддержана Российским фондом фундаментальных исследований. Грант № 05-06-80062а.