© А.В.Коганов
ЭМПИРИКО-ЭТАЛОННЫЕ ОСНОВЫ МАТЕМАТИЧЕСКИХ ТЕОРИЙ
А. В. Коганов
Научно-исследовательский институт системных исследований Российской Академии Наук (НИИСИ РАН); Москва, 117218, Нахимовский пр. 36, корп. 1, т.(095)-143-2370, (095)3324818, e-mail: koganow@niisi.msk.ru
Работа выполнена при содействии Российского фонда фундаментальных исследований (РФФИ), проект № 01-01-00754
1. Введение.
Характерной особенностью современной науки стало использование математического языка для регистрации, обработки и интерпретации экспериментальных данных. Этот процесс, получивший название математизация, позволяет снизить уровень субъективности оценок эмпирических результатов, обеспечить адекватную передачу данных между исследовательскими центрами, оценить надежность сделанных выводов, которая никогда не бывает абсолютной в науках о природе. Но наиболее эффективна математика в становлении научного языка, обеспечивающего однозначную интерпретацию описаний объекта исследований. При этом объект может иметь много описаний и моделей, несовместимых друг с другом, но каждое описание не порождает внутренних противоречий. Весьма распространено применение математики для построения прогнозов, как при использовании результатов науки в практической деятельности, так и в самой науке при подготовке новых исследований. Прогноз математической модели может уступать человеческой интуиции в учете скрытых или трудно поддающихся формулировке факторов, но зато явно указывает причинные связи предсказания с известными фактами и принятыми гипотезами. Это позволяет использовать модель, даже в случае ошибки прогноза, для корректировки научных представлений о прогнозируемом объекте. Интуитивные прогнозы в случае ошибки совершенно бесполезны.
В то же время сама математика в последние десятилетия приобрела тенденцию к самоизоляции своих "чистых разделов" от прикладных работ. Видимо, это связано с высокой сложностью современных внутренних проблем математики, решение которых требует полного сосредоточения исследователей на логической структуре формальной постановки задач. Эта тенденция носит субъективный, и скорее всего, временный характер, однако сегодня разрыв между прикладной и чистой математикой очень ощутим.
Все сказанное делает понятным интерес широкого круга ученых разных специальностей к основаниям математики. Оставляя математические тонкости профессионалам математикам, представители других наук хотят понять связь математических абстракций со своими эмпирическими реальностями. И прежде всего, необходимо устранить несоответствие интерпретации терминов в математике и ее прикладных областях.
В данной работе будет прослежена динамика проникновения математических описаний и моделей в некоторые области эмпирического знания. Кроме того будет исследовано происхождение логики и современного математического языка из непосредственного человеческого опыта, путем эталонизации смысла некоторых терминов и методов составления из них осмысленных конструкций. Интересно проследить также эволюцию социальной и психологической среды, в которой развивались контакты математиков и эмпириков.
2. Особенности математического мышления.
Выделение математики из других наук произошло по способу конструирования объектов. Это был длительный (и еще далеко не завершенный) процесс постепенного отделения умозрительного образа внешнего мира человека от его сенсорного прототипа.
Все другие науки берут объекты, уже существующие во внешнем мире (или создают их там) и закрепляют за ними специальные термины. Свойства объектов не вытекают из тех слов, которыми они названы, а выясняются только в результате натурных наблюдений или направленных экспериментов. Слова, которыми описываются эти свойства, только фиксируют опыт оперирования с реальными телами или процессами, и не являются следствием названия. По сути, описание объекта — это тоже название природных объектов, являющихся частями или свойствами исходного.
В математике сами объекты создаются из интерпретации слов и их сочетаний, входящих в словесное определение термина, называющего этот объект. Все свойства объекта следуют из этого определения и выявляются в процессе логического (в переводе с латинского — словесного или законного) анализа. По сути, и это важно, логическая выкладка является в математике экспериментом над определением. К этой интерпретации логики мы вернемся позже. Пока же заметим, что подобное отношение к словам и к реальности — это уникальное свойство математики среди других наук.
Даже философы, по сути своей, безусловно, теоретики, в своих рассуждениях все время явно или между строк обращаются к наблюдаемым и известным свойствам реалий, стоящих за терминами и именами. Если речь идет об абстрактных классах, то в качестве аргументов используются известные или интуитивно правдоподобные свойства отдельных представителей этих классов в их реальном, а не умозрительном, воплощении.
Только в математике нет наблюдений вне рассуждений. Если в математическом определении объекта не учтено какое-то его очевидное свойство, то использовать это свойство в логической выкладке категорически запрещено. Например, в классической геометрии нельзя пользоваться шириной линии или площадью точки, хотя в любом воплощении эти параметры, очевидно не нулевые. Такое положение вещей может иногда приводить к сильной неадекватности математических выводов с интуицией или опытом. Однако, именно это несоответствие и будет аргументом для модификации определения. Ценность адекватной математической модели не столько в ее свойствах (которые часто известны заранее из опыта над прототипом модели), сколько в тех факторах, которые пришлось учесть, формируя подходящее для использования математическое определение. Это и есть существенные свойства объекта, определяющие его наблюдаемое поведение.
Надо отметить также сильное отличие математики от искусства, где, казалось бы, тоже истинной считается выдуманная реальность, описанная словами, звуками или изображениями. Художник предполагает за каждым человеком право на личную интерпретацию его произведения. Однозначность интерпретации противопоказанна искусству именно потому, что превращает искусство в математическую схему, неизбежно упрощающую реальный мир. А творчество зрителя в художественном восприятии досказывает то, что не уместил в своем произведении автор.
Такая свобода в математике означала бы смерть этой науки. Вся ценность математики в объективности ее построений, то есть в независимости свойств определяемых понятий от субъекта восприятия. Объективизация математических построений выше, чем у реальных наблюдаемых явлений, на которые возможны, иногда, несовместимые точки зрения. Каждый математик прикладник знает, что выяснение смысла слов, употребляемых специалистами в других областях, приводит к их лавинообразному размножению путем деления терминов на уточненные варианты. Достижение однозначности интерпретаций окупается буквальной вечностью математических объектов. Квадрат для учеников Пифагора означал ровно то же, что и для учеников современных школ. За две с половиной тысячи лет математическое понятие не изменилось. За это время рухнули циклопические сооружения древних, которые мы теперь наблюдаем только в руинах, потеряла облицовку пирамида Хеопса, взорвалось множество звезд, рушились империи, пересохли реки, изменился климат... Самой прочной оказалась словесная математическая конструкция.
3. Как достигается однозначность интерпретации.
Распространено мнение, что уточнить интерпретацию фразы можно добавив к ней еще несколько фраз. Против этого возражали многие писатели, считая многословие признаком бездарности и беспомощности автора. Точность достигается не большим числом косноязычных слов, а предъявлением минимального числа ясных образов. Для литературы это блестяще показал А. П. Чехов в “Чайке”, описав, устами персонажа, ночь бликом луны на колесе телеги.
Что касается науки, то бесконечное уточнение смысла слов через другие слова может закончиться только исчерпанием словарного запаса или порочным кругом зацикливания определения слова, через него самого. Слов конечное количество, и поэтому любая цепочка уточнений приведет нас к словам, которые уже нельзя объяснить словами. Как же вводить интерпретацию самых начальных слов, выражающих базовые понятия науки? Выход только один. Смысл начальных понятий надо пояснять предъявлением реальных предметов, действий или процессов непосредственно от учителя к ученику. И если мы хотим добиться однозначной интерпретации, то требовать это надо от процесса натурного обучения основам математики.
Такие неопределяемые, а предъявляемые понятия, обладающие свойством адекватного восприятия большинством людей, естественно назвать математическими эталонами, по аналогии с их метрологическими собратьями в Палате мер и весов. Специальное исследование, проведенное автором, позволило выявить те эталоны, которые легли в основание современной математики. Кроме того найден ряд ранее использовавшихся, но потом признанных недостаточно однозначными, эталонных понятий, которые до сих пор применяются для предварительного пояснения смысла строгих определений и формирования эффективной математической интуиции. Например, интеграл — как площадь под графиком функции.
4. Перечень математических эталонов.
1) Носитель информации ( место записи теории и-или объекта).
Формируется предъявлением бумаги и записи на ней или других средств занесения и хранения символов. Эталонные свойства:
1.1) Носитель имеет места, где можно записывать любые символы;
1.2) Этих мест достаточно для данной теории;
1.3) Эти места адресуемы и упорядочены ( обычно порядок линейный);
1.4) Сделанная запись неизменно сохраняется во времени, но может быть изменена волевым путем по мере развития теории.
***
2) Алфавит теории ( набор различимых и узнаваемых символов).
Формируется предъявлением букв, цифр, иероглифов, особых значков. Эталонные свойства:
2.1) Алфавит состоит из набора значков, одинаково узнаваемых и различаемых всеми людьми; Расширение набора допустимо только такими знаками, которые не путаются с ранее введенными. Поэтому эталоном является не сам знак, а весь набор знаков.
2.2) Два значка либо всегда отождествляются, либо всегда различаются;
2.3) Каждый значок может тиражироваться на носителе в количестве достаточном для теории и в форме, отождествляемой с исходной.
***
3) Линейный порядок ( последовательность элементов).
Этот объект интерпретируется как во времени, так и в пространстве.
Его свойства похожи на аксиомы натурального ряда чисел. Имеется первый объект. За каждым объектом либо имеется следующий, либо он последний. К любому объекту порядка можно подойти от первого элемента последовательными переходами к последующему элементу.
Формируется предъявлением пространственных рядов или временных последовательностей действий и событий. Вводит слова "раньше, позже, ближе, дальше, выше, ниже, больше, меньше" и т. п. Имеются нейрофизиологические данные о врожденном характере интерпретации и понимания линейного порядка человеком.
***
4) Совокупность элементов.
Формируется как эталон предъявлением конечных наборов предметов или бесконечных наборов точек в геометрических фигурах. Очень тесно связан с эталонами алфавита и линейного порядка.
Свойства конечных совокупностей включают в себя выполнимость основных операций над множествами, таких как объединение нескольких совокупностей в одну, или выделения совокупности объектов, входящих сразу в несколько указанных совокупностей. Можно формировать совокупности предметов входящих в одну заданную совокупность, но не входящих в другую. Можно формировать совокупности из совокупностей.
Однако все эти действия эталонизируются только для конечного набора предметов. Аналогичные свойства бесконечных совокупностей не являются эталонными и вводятся уже на уровне логических построений.
***
5) Произвольный выбор из данного множества альтернатив.
Формируется выполнением ответных действий на просьбу "выбери один предмет из этого набора". Имеется прямая связь с эталоном совокупности, но важным собственным свойством является проявление волевого фактора в действии, происходящем в условиях неопределенности задания. Например, реакция на просьбу взять красный шар из набора разноцветных шаров не входит в формирование произвольного выбора (это относится к эталону цветового алфавита). А вот задание "взять один шар" из того же набора уже включает принятие волевого решения.
***
6) Шаг рассуждений или построений
Формируется демонстрацией вычислений, геометрических, конструкторских или логических построений, как элементарный этап этих действий. В последнее время возникла интерпретация через шаг алгоритма или команду программы компьютера. Этот эталон связан с интуитивным образом времени. К существенным свойствам этого эталона нужно отнести требование предварительной подготовленности тех объектов, которые требуются для выполнения шага. Кроме того шаги образуют линейный порядок, подготавливая условия для выполнения последующих шагов.
***
7) Подстановка / таблица / отображение.
Формируется демонстрацией замены части текста на другой текст или предмета на предмет по описанным в форме таблиц правилам. Тесно связан с носителем информации и алфавитом. Все вычисления, логические правила и операции вводятся через этот эталон.
***
8) Тиражирование математического объекта.
Формируется демонстрацией копий геометрических структур, графических схем, текстов описаний математических объектов, наглядных пособий и т. п. Эталонным является сохранение в копии всех математических свойств оригинала при различимости копии и оригинала. Кроме того, повторная копия от копии и разные копии оригинала признаются математически равноценными и попарно различимыми. Над разными копиями можно производить независимые действия, которые влияют на свойство только одной копии. Измененная копия перестает быть копией исходного объекта, приобретая новые математические свойства.
***
9) Обязательное действие в описанной ситуации.
Предполагает обучение распознаванию ситуации по описанию и запрет на все действия, кроме предписанного. Кроме того, имеется эталонная активация действия или запрет на бездействие. Этот эталон включает в себя и понятие запрета. Обучение обычно ведется на играх (обязательные ходы) и использует более ранние элементы воспитания детей.
***
10) Заучивание текста, действия или образа человеком.
Этот эталон независим от остальных, хотя может показаться, что он - только частный случай записи на носитель. Фактически, в математике только заученная человеком информация может играть активную роль. Относится сюда и обучение эталонам.
***
11) Дополнительные эталоны.
Введенных эталонов 1-10 достаточно, чтобы построить современный математический язык. Однако имеются и другие эталоны, которые сегодня используются в интуитивном мышлении математика, причем для построений, выполненных с помощью этих дополнительных эталонов, существуют стандартные средства перевода на язык, их не использующий. Однако, как эталоны они независимы, и такая редукция связана с ограничением на использование их свойств при "современном уровне строгости" в математике. Однако эти дополнительные свойства часто оказываются очень удобными для усиления человеческой интуиции при постановке и решении задач. К таким дополнительным эталонам нужно отнести:
11.1) эталоны простейших геометрических форм (круг, квадрат, отрезок прямой, треугольник, угол, пересечение отрезков);
11.2) геометрические преобразования на плоскости типа сдвига, поворота, совмещения точек фигур при сдвиге, построения циркулем и линейкой;
11.3) отождествление интеграла функции с площадью под ее графиком, а дифференциала - с касательной к графику;
11.4) изображение связей стрелками на графе;
11.5)понятие поощрения и наказания при описании цели действия. Само понятие цели и успеха также является вспомогательным эталоном, однако здесь трудно говорить о строгой однозначности интерпретации, если не введена система поощрений.
Имеется ряд других наглядных приемов, обычно не приводящих к серьезным ошибкам, но помогающих почувствовать математическую задачу.
***
Нижеследующие эталоны не используются в математической логике непосредственно, но совершенно необходимы математику на семантическом уровне формальной логики. Без них математика не могла бы быть понята.
12) Пример для общего понятия (частный случай).
Формируется демонстрацией конструктивных примеров объектов, свойства которых удовлетворяют всем требованиям словесного определения класса объектов. При обучении используются задачи на построение таких примеров для заданных определений.
Важным эталонным свойством является неоднозначность перехода от общего определения к частному объекту. Другое эталонное условие — наличие четко сформулированных свойств, определяющих класс. На стадии обучения возможна игра с использованием побочных смыслов слов, входящих в определение.
Этот эталон предшествует логике, и фактически лежит в основе понятия интерпретации математической теории.
***
13) Обобщающее логическое определение для набора объектов.
Формируется обучением выделять общие признаки у разных конструктивных или реальных объектов. Важным эталонным свойством является неоднозначность перехода от набора объектов к общему определению. При этом свойства определяемого класса зависят только от определения, а не от исходных объектов. В частности, при изменении определения могут меняться некоторые примеры объектов класса, но исходные объекты при правильном определении всегда являются примерами. Указанные неоднозначности означают, что эталоны примера и определения не являются взаимообратными операциями, но психологически они взаимодополнительны.
***
14) Введение эталона.
Имеется еще не вполне сформированный Эталон Введения Эталонного Понятия. Ближе всего к нему в современной науке подошли, видимо, метрологи и педагоги. Но в математике он никогда не использовался в явном виде. Главным признаком эталонности термина является адекватность его трактовки разными людьми. Это проверяется совпадением действий и их результатов при выполнении разными людьми инструкций, в состав которых входит этот термин. При обнаружении неадекватности необходимо обратить на нее внимание обучаемых и дать дополнительные разъяснения на уровне словесных описаний или демонстрации с использованием пособий и тренажеров. Последнее очень распространено в математике при обучении геометрическим и программистским терминам.
***
Можно только предполагать, что расширение прикладного использования математики сделает актуальным систематизацию приемов эталонизации терминов. Видимо, эта область всегда будет относиться к метаматематике.
5. Как строятся математические модели .
Последовательное построение современной математической логики из введенных эталонов не входит в задачу данной статьи и автор предполагает знакомство читателя с понятием правил вывода, поля вывода, логических операций и аксиоматики теории. Существенным для понимания будет тот факт, что на каждом шаге логического вывода в традиционных логиках выбор очередного правила вывода и его операндов осуществляется произвольно из всего наличного на этом шаге набора. При этом набор правил вывода остается неизменным, а меняется состав возможных операндов вывода в поле вывода.
Общий взгляд на нестрогое описание модели состоит в том, что в процессе вывода на носителе будут возникать недопустимые с точки зрения принятой логики сочетания объектов. Задачу предматематики теперь можно сформулировать так: каким образом следует менять систему аксиом при обнаружении нестрогости модели. При этом желательно не потерять тех теорем, которые можно получить из прежних аксиом в допустимых состояниях. Уже в этой очень абстрактной формулировке видно, что при появлении нестрогости приходится отказываться от идеи произвольного выбора очередного правила вывода и выполнить какие-то обязательные "профилактические" действия. Кроме того, следует ожидать неоднозначности возможных модификаций теории, что означает разветвление теории на несколько альтернативных вариантов. Эта бифуркация теории на шаге проявления нестрогости модели, соответствует ветвлению функции истинности на множестве возможных утверждений о свойствах моделируемого объекта. При моделировании природных явлений такое расщепление обычно отражает только степень нашей неосведомленности и предполагает в дальнейшем экспериментальное уточнение модели. Но при изучении произведений искусства именно в этом разветвлении интерпретаций и может заключаться главная информация.
К модификации теории можно сразу выделить два подхода: интуитивный и методический. Интуитивный подход содержит только один явно сформулированный шаг: при обнаружении в поле вывода нестрогости ( недопустимого сочетания записей ) прекратить дальнейший логический вывод. Далее следует совершенно не эталонная рекомендация искать новые аксиомы, но для каждой предложенной аксиоматики требуется возобновить вывод в эталонной логике. Этот путь очевиден, но его нельзя считать эталонным предматематическим процессом в силу неопределенности способа поиска аксиом.
В методическом подходе регистрация нестрогости теории приводит к изменению поля вывода в рамках специальной эталонной конструкции. В результате формируется новая аксиоматика и система определений, возможно в нескольких вариантах, а также новые правила вывода, позволяющие в дальнейшем избегать той же самой нестрогости. При появлении новой нестрогости процесс повторяется. Такой метод будет эффективен, если удастся наращивать теорию, не теряя того, что получено до возникновения нестрогости. В этом случае мы уже имеем модель предматематики на эталонном уровне. Однако, следует понимать, что никакой метод не даст всего, что можно сделать творческим путем, и за эталонность действий прийдется платить упущенными вариантами теории. В то же время методический путь интересен тем, что для борьбы с нестрогостью используется сама логика, и поиск строгой модели становится предметом изучения.
6. Как определить саму математику?
Попыток определения математики в истории науки было множество. Была даже попытка сделать обязательным для всех и всегда определение Ф. Энгельса: “Математика — это наука о количественных соотношениях”. По иронии истории именно современник Ф. Энгельса, логик Дж. Буль, ввел в обиход совершенно неколичественную алгебру высказываний, за которой последовали многочисленные разделы математики, далекие от чисел.
Отражением сложности этого вопроса явилась позиция К. Ф. Гаусса, предложившего считать математикой то, что интересует выдающихся математиков. Хотя такое определение, конечно, было шуткой, в нем заложен большой потенциал. Математика определялась не логически, а эмпирически, с использованием самих математиков в роли “измерительных приборов”.
Физик теоретик Р. Фейнман неоднократно указывал, что есть хорошая и плохая математики. Причем используются обе, потому что природа не позволяет все свести только к идеальным постановкам задач. В "плохой математике" возможно введение дополнительных постулатов по ходу рассуждений, исходя из нестрогих аргументов, не вытекающих из исходных определений, но имеющих обоснование в прикладной интерпретации теории. Самое неприятное, что эти постулаты не учитываются в других местах той же теории. Такие рассуждения — не редкость в физике и технике. Иногда они поразительно эффективны. Но если дополнительные постулаты не могут быть введены как общие аксиомы для всей теории, математической модели не возникает, и их следует рассматривать только в качестве правдоподобных пояснений в подгонке результата под заранее известный ответ.
Думаю, не будет большой натяжкой считать математической любую теорию, построенную на использовании только эталонных терминов, производных от них определений и эталонного логического вывода. Однако эталонизация теории не означает эталонизацию мышления математиков-людей. Поиск самих аксиом, определений, теорем и их доказательств — дело глубоко творческое и неординарное.
В заключение раздела, приведу спонтанное высказывание одного школьного учителя математики: математика — это то, о чем людям удалось договориться.
7. Вариант ветвящейся логики для формирования аксиоматики.
Предлагаемый метод пригоден для модификации любой из используемых в математике логик. Однако, учитывая, что целью статьи является не формальная общность результата, а содержательная ясность метода, выберем в качестве базы классическую формальную логику с двузначной истинностью: И - истина, Л - ложность. В качестве L-объектов будем рассматривать высказывания. В поле вывода будут помещаться высказывания с пометкой вычисленного для них значения функции истинности, которое будем называть рангом высказывания:
номер/ ВЫСКАЗЫВАНИЕ /истинность;
При таком подходе в поле вывода могут появляться и высказывания, ложные в данной теории, но с рангом /Л. Исходные аксиомы имеют ранг /И. Для проведения анализа с использованием предположений можно ввести дополнительно ранги условной (предполагаемой) истинности: /?И, /?Л. Естественно, все выводы, полученные с использованием высказываний, имеющих условную истинность, имеют условный ранг. Этот ранг используется, например, при доказательстве утверждения “методом от противного”. Все объекты в поле вывода располагаются в порядке появления ( номера идут подряд). Противоречие определим, как одновременное наличие в поле вывода пары объектов вида i/Х/И; j/Х/Л; или i/Х/И; j/не Х/И; где Х - высказывание, а номера несущественны. Операции "и", "или", "не", "следует" определяются известными таблицами истинности и правилами вывода. При появлении в поле вывода противоречия будем регистрировать нестрогость теории.
Для обработки обнаруженной нестрогости нам потребуются дополнительные значения функции истинности: /ПИ , /ПЛ - предварительная истинность или ложность; /Д - доминирующая аксиома. Смысл этих рангов будет разъяснен ниже. Начиная с шага обнаружения нестрогости в логике начинают работать особые операции, применение которых обязательно в оговоренных ниже случаях. Такие обязательные операции будем называть форсированными. Если противоречие имело указанный выше вид, то поле вывода форсированно удваивается с сохранением в каждом экземпляре всех утверждений полученных до противоречия. В один экземпляр форсированно вводится новая аксиома доминирующего ранга: Х/Д; , а в другой экземпляр - аксиома того же ранга (не Х)/Д; Также, как и исходные аксиомы, доминирующие рассматриваются, как истинные утверждения и в таблицах истинности ранг Д заменяется на И. Но теперь на каждом поле вывода строится своя теория и в ней действует форсированное правило: если утверждение противоречит доминирующей аксиоме, оно устраняется из теории. Вначале форсированно осуществляется изъятие из поля вывода всех ранее возникших в нем противоречий с доминирующей аксиомой ( возможно и удаление некоторых исходных аксиом). Для этого ранги всех утверждений в поле вывода заменяются на предварительные и, если утверждение сохраняется в теории, ему возвращают его основной ранг. Затем на каждом шаге вывода новое утверждение получает предварительный ранг и форсированно проверяется на противоречие с доминирующими аксиомами данной теории и если оно есть, то это утверждение удаляется. Если противоречия нет, то предварительный ранг заменяется на соответствующий основной. Таким образом, повторно это противоречие в каждой из новых теорий возникнуть не может. В то же время мы сохраняем альтернативные возможности построения теории, но на разных полях вывода. При возникновении в такой теории нового противоречия произойдет форсированно новое раздвоение теории и появятся новые доминирующие аксиомы. Таким образом, при нестрогой исходной аксиоматике возникает дерево альтернативных теорий, отличающихся составом доминирующих аксиом. Это соответствует многолистной функции истинности, и каждая ветвь теории отслеживает один ее лист. В зависимости от исходной аксиоматики ветвление теорий может быть конечным или бесконечным.
Выше был рассмотрен самый простой случай текстуального противоречия L-объектов. Однако, в разрешимых логиках можно усилить конструкцию, проверяя новые объекты на неэквивалентность отрицанию доминирующих аксиом. Разумеется, это потребует больших вычислений. В неразрешимых логиках или теориях такой подход требует специальной организации расчетов на определение эквивалентности L-объектов, так, чтобы не допустить бесконечно долгого шага вывода. Это может привести к установке предварительного значения истинности у какого-то объекта на неопределенно большое число шагов вывода. В этом случае, любой вывод с использованием этого объекта дает предварительный результат, который нельзя перевести в основной ранг до разрешения исходного объекта. Для этого нужно предусмотреть в поле вывода систему ссылок между зависимыми L-объектами. Возможно, проще запретить вывод с предварительным рангом ( кроме расчетов по установлению эквивалентности).
8. Непротиворечивость метода расщепления теорий.
Рассмотрим вопрос о том, не возникают ли при использовании описанного метода новые первичные противоречия, кроме заложенных в исходные аксиомы. После построения разветвленной теории типов внутренняя непротиворечивость теории сводится к непротиворечивости арифметики путем построения теоретико-множественной модели этой теории. Модель формальной логики строится таким образом, чтобы каждому высказыванию в поле вывода соответствовало подмножество-интерпретация в пространстве элементарных интерпретаций. При этом конъюнкции высказываний соответствует пересечение интерпретаций, дизъюнкции — их объединение, отрицанию — дополнение до всего пространства, а следованию — вложение интерпретации причины в интерпретацию следствия. Каноническая модель логики для высказываний, записанных в заданной грамматике, представляет собой формальное пространство всех правильно построенных высказываний, и в качестве интерпретации высказывания берется множество всех высказываний, из которых оно формально следует, а его отрицание не следует. Известно, что если высказывание влечет хотя бы одно противоречие, то оно влечет и все противоречия. Это доказывается формальной выкладкой, не зависящей от грамматики конкретной теории. Значит, такие высказывания не войдут ни в одну из интерпретаций высказываний, и их собственные интерпретации будут пусты. Отбросим их из пространства интерпретаций. Тогда для высказывания, имеющего непустую интерпретацию, дополнительное множество интерпретирует его отрицание. Остальные свойства выполняются тавтологично. Из аксиом следует теория, состоящая из всех высказываний, в интерпретации которых содержится пересечение интерпретаций всех аксиом. Если аксиомы непротиворечивы (и только тогда), теория содержит не все высказывания. Противоречие в аксиомах означает, что пересечение их интерпретаций пусто, и тогда в этой теории все высказывания истинны (поскольку каждое множество имеет пустое подмножество) - это модельная интерпретация известного факта из логики.
Рассмотрим, что происходит с интерпретациями при расщеплении истины. Если аксиомы непротиворечивы, то ситуация совпадает с описанной выше. Если же возникло расщепление теории доминирующими аксиомами Х/Д; и (не Х)/Д; , то каждая из них в своей теории исключает другую из множества допустимых интерпретаций. Поэтому получить высказывание с пустой интерпретацией (Х и не Х)/И оказывается невозможно.
Устраняются также те высказывания, которые распознаются выбранным критерием допустимости, как влекущие отрицание доминирующей аксиомы. При этом могут сохраниться некоторые такие высказывания вплоть до получения следующего противоречия и нового расщепления аксиоматики.
Каждое из противоречий в любой из ветвей теории получается в результате вывода на основе правил исходной (базовой) логики из исходных и доминирующих аксиом. Но каждая доминирующая аксиома была получена выбором одного из двух высказываний, полученных тем же способом. Таким образом любое высказывание в поле вывода каждой из построенных теорий могло быть получено из исходных аксиом по базовым правилам вывода без прохода через противоречие. Поскольку любой вывод без прохода через противоречие может быть осуществлен, то совокупность всех L-объектов во всех получаемых при разветвлении теориях совпадает с L-объектами, которые можно получить известным методом границ, прерывающем цепи вывода при получении парадокса. Однако, при ветвлении теорий эти L-объекты будут размещены по разным теориям, внутри которых нет парадоксов.
В частности, это означает, что не возникло новых возможных интерпретаций и новых противоречий, по отношению к выводу в базовой логике.
В теориях, полученных методом расщепления аксиоматики, не может содержаться противоречий ни на каком завершенном шаге вывода, поскольку каждое из возникающих противоречий форсировано подавляется (после получения) соответствующим расщеплением теории и больше не возникает.
9. Потенциал эталонного порождения множеств.
В теоретической физике часто возникает вопрос о возможности порождения бесконечных множеств из конечного начального набора объектов. Например, рассматривается возможность порождения всего пространства-времени из конечного числа взаимодействий частиц. Анализ этой постановки задачи, привел к утверждению, что такие конструкции всегда неявно подразумевают наличие некоторого бесконечного ресурса, скрытого за неэталонной терминологией.
Теорема. Эталонная конструкция множества, построенного с использованием только конечного числа N эталонных исходных объектов, может содержать не более 1.5N элементов.
Для доказательства достаточно заметить, что построение каждого нового объекта требует минимум двух эталонных операций: выбор из существующих объектов подмножества, как конструкта нового объекта, и размещения его на элементе носителя теории. Сами шаги вывода тоже являются ресурсом теории, поэтому на формирование нового объекта расходуется три элемента ресурса: два шага и одно место. Всего N исходных объектов могут породить N/3 новых объекта. Сумма соответствующей геометрической прогрессии равна 1,5N , что и оценивает сверху потенциал эталонного порождения множества.
Проведенный выше анализ ставит вопрос о правомерности рассмотрения бесконечных множеств в рамках эталонной логической теории. Начальный эталон совокупности объектов предполагает либо ее конечность либо буквальную обозримость неопределенно большого числа точек в геометрических фигурах. С другой стороны, эталон носителя информации в любом воплощении допускает только конечное число мест. Фактически, это означает, что бесконечное множество не может быть непосредственным эталонным объектом. Проблемы, порожденные теорией множеств Г. Кантора, связаны именно с тем, что множеством считалась любая формально описанная конечным числом признаков совокупность объектов, определения которых удовлетворяют принципу исключенного третьего. Оказалось, что такие описания сами по себе не всегда эталонны и допускают неоднозначные трактовки.
Парадоксы теории множеств, построенные Б. Расселом, основаны на одновременном использовании разных трактовок одного описания. Однако исторически первым был парадокс Г. Кантора о самом большом кардинале, за которым должен следовать еще больший кардинал. Он также связан с неэталонностью операции тиражирования объектов в бесконечном числе. Формально, можно образовать множество всех существующих множеств. Это самое большое множество уже содержит все возможные объекты, и добавить к нему нечего. Но нет запрета на тиражирование, и это позволяет столь же формально получить копии всех подмножеств этого множества и образовать из них новое множество. Диагональным процессом доказывается, что мощность такого множества всегда больше чем исходная, если число элементов исходного множества больше двух. Таким образом, неэталонное применение операции тиражирования порождает противоречие. Это тиражирование в классической теории множеств неявно присутствует в аксиоме Цермело.
С другой стороны, даже минимальный бесконечный тип — множество всех натуральных чисел — предполагает бесконечный носитель информации, который не входит в исходную эталонизацию. Это наводит на мысль, что каждое увеличение мощности множества, сверх максимально постулированного в теории на предыдущих шагах, требует новой независимой аксиомы существования. Это относится даже к конечным числам, что хорошо известно математикам вычислителям, постоянно работающим под угрозой переполнения памяти компьютера. С другой стороны, нет никаких оснований запрещать объединение в множество объектов, каждый из которых имеет определение через базовые эталоны. Последнее обстоятельство следует рассматривать, как разрешение на введение аксиомы существования таких множеств и их мощностей.
Таким образом, эталонизация множеств требует кроме общей аксиоматики теории еще и отдельного постулата существования для каждой из конкретно рассматриваемых мощностей, причем вводить ее надо как мощность множества предварительно строго определенных объектов. При таком подходе в теории, основанной на конечном логическом выводе теорем, может быть рассмотрено только конечное число разных мощностей множеств. Это очень близко подходит к теории типов Б. Рассела, но, фактически, требует еще большей дисциплины. Парадоксы при таком подходе, вероятно, не возникают, но по ходу рассуждений может потребоваться шаг введения нового постулата существования нужной мощности. Следовательно, эталонная теория множеств может существовать только в форме ветвящейся аксиоматики.
Если требовать строгого определения линейного порядка всех введенных мощностей, то применима теорема П. Коэна о непротиворечивости теории при условии непротиворечивости натуральной арифметики. Наличие такой упорядоченности следует проверять форсированной операцией, применяемой после каждого введения нового постулата мощности. Эта операция должна быть эталонно определенной процедурой, которая устанавливает место новой мощности в ряду мощностей ранее введенных в теорию. Если эта процедура окажется неприменимой к новому множеству, определяющему вводимую мощность, то его следует удалить из теории. Фактически, при таком подходе теорема о непротиворечивости усиливается: эталонная теория множеств не содержит противоречий, если нет противоречий в арифметике на любом конечном множестве натуральных чисел.
Покажем, как исчезает парадокс Г. Кантора при эталонном подходе. Термин "МНОЖЕСТВО ВСЕХ МНОЖЕСТВ"(МВМ) в эталонной теории может означать только множество всех введенных ранее множеств, как объектов, определенных на поле вывода теории. Иначе будет нарушено требование эталонности описания всех элементов вводимого множества. Но тогда множество его подмножеств ПМВМ будет состоять из новых объектов, определяемых, например, как бинарные функции на МВМ. Поскольку мощность ПМВМ выше всех мощностей ранее введенных множеств, то требуется введение аксиомы существования носителя для него. Но противоречия уже не возникает, поскольку новое множество введено в поле вывода после формирования МВМ, а повторное введение множества всех множеств будет относиться уже к новой аксиоматике, и отлично от МВМ.
В заключении раздела дадим ответ на вопрос, что фактически происходит в теориях, порождающих бесконечные пространства из конечного числа объектов? Как показано выше, само существование нужной мощности приходится постулировать. Однако для этого необходимо предварительно указать эталонный формат записи каждого элемента формируемого множества. Именно такой формат, обычно в виде формул некоторой алгебры, и предлагается в качестве "порождения точек пространства". Можно сказать, что эти теории не порождают новую бесконечность, но форматируют постулированную.
10. Приоритетная эталонизация.
Природа большинства начальных эталонов математики в настоящее время не выяснена. Можно предположить физиологическую основу для некоторых эталонных признаков, таких, как линейность расположения мест на носителе информации, свойств линейной упорядоченности, осуществимости произвольного выбора, и др. Однако, в ряде случаев, можно говорить об особой эталонизации, не имеющей объективной основы.
Наиболее ярко необоснованность эталонизации видна в выборе стандартных имен для новых объектов теории. Такие имена после первой публикации становятся обязательными к употреблению, и изменить их можно только сложной процедурой оповещения всех заинтересованных лиц и внесения поправок в основные учебники. Еще большей инерцией обладают алфавиты основных языков, которые, практически, не возможно существенно изменить. Математические обозначения основных операций не изменяются столетиями. Их необязательность видна из того, что некоторые операции веками имеют два и более обозначений (например, производная функции, скалярное произведение векторов и даже простое умножение чисел).
Этот тип эталонов роднит математику с другими науками, где названия и обозначения столь же произвольны. Достаточно вспомнить имена созвездий в астрономии. В математике эти эталоны не являются базовыми, поскольку их можно синтезировать на носителе из алфавита, а знаки входят в эталонный алфавит. Но они совершенно необходимы для обеспечения научного общения внутри математики и с представителями других областей. Важность этой функции имен и знаков отмечена даже в законодательстве, охраняющем авторские права на эмблемы товаров и организаций. В математике адекватность имени объекту обеспечивается эталонной подстановкой определения объекта вместо имени при логическом выводе. Во всех остальных видах деятельности людей это соответствие специально не определяется, а является основным смыслом используемого языка.
Установление таких эталонов связано с динамикой развития и носит исторический характер. Общепринятыми именами и обозначениями новых объектов обычно становятся первые предложенные варианты. Однако из них выбираются наиболее выразительные и социально подходящие. Часто укореняются жаргонные термины, а официально закрепленные становятся малоупотребительными (вспомним слова "метро" и "метрополитен"). В математике жалобы на неудачные обозначения не редкость, но меняются они реже, чем в какой либо другой науке.
Выявление законов установления этих эталонов — задача, скорее, психологии и социологии. Но важность их для математики неоспорима. Поскольку для их формирования главным фактором является приоритет, в дальнейшем будем называть их приоритетными эталонами, а процесс их становления — приоритетной эталонизацией.
Особую роль приоритетные эталоны играют в кибернетике и информатике. Алгоритмические языки фактически являются такими эталонами. Из сотен изобретенных языков программирования практика отобрала около десятка, оказавшихся удобными для программистов. Другой класс приоритетных эталонов составляет дизайн интерактивных систем. Сегодня наиболее распространены принципы многооконного интерфейса. При этом попытка отказаться от двухоконного интерфейса в системе Windows в пользу более развитого многооконного вызвала неудовольствие пользователей, и в систему ввели двухоконные элементы. Этот пример показывает, что в приоритетной эталонизации имеются существенные объективные компоненты, которые пока учитываются чисто эмпирически. Однако важную роль играет и активность в распространении продукции фирмы изготовителя, успевающей навязать свой стандарт большому числу пользователей. Не обходится без парадоксов: в современных алгоритмических языках операция присвоения значения переменной имеет около десяти разных обозначений.
Вероятно, некоторые принципы построения базовых эталонов возникли путем выделения объективных факторов в приоритетной эталонизации. Например, все алфавиты построены как комбинации стандартных элементов типа крючков, петель, кружков, крестов и точек.
Одним из способов находить логические эталоны может оказаться выделение общих понятий в разных языках, особенно древних и у мало общавшихся народов. У всех народов имеются понятия "прямой", "кривой", "близко", "далеко", "быстро", медленно". Это подсказка: порядок и метрика близки к первичным эталонам.
Можно заключить, что ранняя стадия эталонизации понятий — это приоритетная эталонизация, позволяющая постепенно выделить объективно предпочтения человека, как биологического вида, в каждой области его деятельности.
11. Время в математике.
Как процесс построения теорий и накопления знаний и методов математика всегда была связана с временем. Кроме того, все математические методы подразумевают последовательную выкладку или конструкцию во времени. Тем не менее от Евклида и Аристотеля идет традиция изгнания из математических теорий понятия времени и его явного упоминания. Это было связано с представлением о времени, как о предельно нестабильной составляющей нашего мира, которая никогда не повторяет своего состояния дважды. Математические же теории строились навечно. Даже аксиомы считались самоочевидными фактами, навечно установленными богами. Эта традиция перешла в христианскую Европу через канонизацию Аристотеля.
Однако, алгоритм измерения отрезков Евклида явно содержал развернутую во времени последовательность действий, да еще с условным ветвлением, зависящем от результата предыдущего действия: если единичный отрезок не уложился в измеряемом отрезке целое число раз, то его надо уменьшить в десять раз и продолжить прикладывать к остатку. Но соответствующая теорема даже не содержала намека на время: каждый отрезок представим десятичной дробью через единичный.
Такое противоречие методов и формулировок сохраняется в чистой математике до сих пор, и не вызывает протестов, как профессиональный стиль. Отдельно формулируются процедуры, а отдельно теоремы, утверждающие существование этих процедур. Как правило, сама конструкция процедуры при этом составляет доказательство теоремы. Скрыто время существовало в математике в форме шагов вывода и вычислений или как формальный числовой параметр модели, которому разрешалось меняться только в одну сторону. Возможность изменять этот параметр в сторону уменьшения иногда, например в механике, рассматривается как парадокс, требующий объяснения.
Эта забавная ситуация не пережила вторжения программирования в вычислительную практику. К этому времени вера в богоданность и самоочевидность аксиом сильно пошатнулась. Аксиомы стали скорее прагматической потребностью теории, чем безусловными началами знания. Программисты прямо поставили вопрос о реальном времени счета. А теоретикам пришлось задуматься, что получится быстрее: вывести аналитическую формулу или построить алгоритм.
Кроме того, античное представление об уникальности момента времени сменилось осознанием однородности свойств всех моментов. Если воспроизвести совокупность причин, то воспроизведется и следствие. Математика приобрела форму условных утверждений, не претендующих на абсолютность вывода, но только на его обусловленность перечисленными свойствами. Например, теоремы геометрии верны только при условии истинности аксиом данной геометрии. Это также способствовало реабилитации времени в математике.
Другой путь проникновения времени в математическую парадигму, это потребность оценить безошибочность вычислений и доказательств. Увеличение сложности вывода теорем и еще более возросшее число вычислительных операций сделало невозможным непосредственную проверку. Вероятность ошибки проверяющего стала выше, чем у проверяемого, поскольку проверка требует большего числа шагов. В вычислительной практике прочно обосновались статистические методы тестирования программ, явно использующие время. Правильность теоретического вывода, содержащего десятки тысяч элементарных предложений, все чаще проверяется голосованием по группе экспертов в данной области. Фактически, приходится говорить не о правильности доказательства, а об установлении временного статуса необнаруженности ошибки. Динамика явно вошла в математику.
Возникла также область математики, оценивающая надежность вычислительных средств. По сути, нестабильность работы аппаратуры (также, как и ошибка человека в логиго-вычислительной выкладке) означает неэталонность выполняемых операций. Борьба с этим тоже ведется средствами математической статистики и тестирования.
В программирование время входит вместе с его физической мерой. Оценивается метрологическая длительность отдельных операций и их цепочек, возможных при выполнении программы. Для среднестатистическокой частоты операций введена даже новая единица измерения — один флопс (flops). Отличие от традиционных герц заключается в недетерминированной длительности одной операции, и установлении среднестатистического числа операций в секунду. Таким образом, информатика использует математические эталоны совместно с метрологическими. Но в других областях математики до этого не дошло.
Значительно тоньше время проникает в структуру моделей. Метрологическое время обычно вводится в модель как числовой параметр, имеющий стандартную интерпретацию через показания эталонных часов. Этот прием вероятно впервые был сформулирован Декартом, предложившим использовать числовые прямые для всех измеряемых переменных. Тем самым время заменялась на характеристику, имеющую пространственную интерпретацию. Проблемы с обратимостью времени в теоретической механике связаны именно с этим допущением.
Но не всегда эталонное метрологическое время адекватно отражает ритмику и длительность моделируемого процесса. Приложения часто требуют использования событийного времени. Время измеряется числом специально распознаваемых и регистрируемых событий. Эти события отражают специфику процесса, в отличие от внешних тактов универсального метрологического времени. Это могут быть особые воздействия на моделируемый объект или его реакции. Имеется много работ, в которых показано, что в собственной событийной шкале времени несколько процессов имеют одинаковую модель, хотя очень непохожи в универсальном времени. Примером могут служить процессы размножения различных видов животных, имеющие близкие описания, если за единицу времени взять одно поколение.
Введение такого времени требует от математика разработки эталонной логико-измерительной процедуры распознания и регистрации событий. Использование субъективного распознания событий или неоговоренных форм их регистрации в модели может порождать серьезные неоднозначности оценок и прогнозов, лишающие модель ценности. Событийные шкалы времени могут сильно разниться по своим свойствам даже для одного объекта моделирования. Эталоны распознавания событий составляют отдельное направление в современной кибернетике. Их анализ выходит за рамки данной статьи. Но стоит остановиться на различных способах эталонной регистрации событий. Именно с ними связаны главные различия событийных шкал времени.
11.1. Потенциально равномерные событийные шкалы.
Если распознанные события последовательно записываются на носитель информации, а мерой времени считается количество таких записей, то равномерность шкалы времени по метрологическому эталону зависит от статистических свойств самой последовательности событий.
При статистической стационарности процесса возникновения эталонно распознаваемых событий возникает шкала времени, равномерная по метрологической на больших интервалах длительности, за которые происходит в среднем достаточно большое (по критериям сходимости статистики) число событий. Однако на малых длительностях возможны флюктуации темпа хода событийных часов.
Если сама последовательность событий не стационарна по метрологическому эталону времени, то, соответственно, ведет себя и событийная шкала времени. Например, песочные часы пригодны для измерения номинальных метрологических длительностей периода полного пересыпания песка. Однако промежуточные длительности измеряются метрологически не равномерно по числу пересыпавшихся песчинок, поскольку давление на нижние песчинки верхней колбы убывает по мере уменьшения в ней песка. Таким образом, событийная шкала замедляется относительно эталона. Если мерить время развития социума числом технических изобретений, то событийная шкала даст значительное ускорение в периоды НТР, и замедление в периоды интеллектуального упадка.
11.2. Шкалы с потенциально нарастающей разрядкой.
Если регистрируются не все распознанные события, а имеется критерий отбора, то число зарегистрированных событий может замедляться относительно метрологического эталона даже при стационарности процесса их возникновения. Примером таких шкал является регистрация рекордов, то есть событий, имеющих некоторые количественные показатели, превосходящие все ранее зарегистрированные. Если эти показатели распределены в эталонном метрологическом времени стационарно, то метрологические интервалы dt между регистрациями начинают неограниченно возрастать: если F(x) — функция распределения показателя x(i) , то
E{dt(N+1)} = 1/(1-F(max{x(i) | i=1,...,N})) .
11.3. Циклические событийные шкалы времени.
Эти шкалы возникают при учете событий, имеющих числовые характеристики x(i), i=1,2,... . Если их суммировать в циклическом счетчике
T(N)=Summ{x(i) | i=1,...,N} (mod M) ,
то на значение событийного времени T влияют только последние события, произошедшие после последнего сброса счетчика. Выбор модуля цикличности M надо выбирать, исходя из содержательных соображений, чтобы не потерять еще не устаревших данных.
11.4. Событийные шкалы с убыстрением.
Такие шкалы возникают при стационарном потоке событий в метрологическом времени, если одно событие может быть многократно учтено в счете времени. Модельным примером такой шкалы может служить регистрация всех событий с прибавлением к счетчику числа всех записанных событий при каждом распознавании.
T(N)=T(N-1)+N; тогда T(N)=N(N+1)/2 .
Иногда использование шкал этого типа бывает осмысленным, например при учете цены сделок в расчете национального дохода. В цену каждой новой сделки входит цена ей предшествующих.
11.5. Шкалы с забыванием событий.
Такие шкалы возникают, когда события оцениваются с точки зрения их причинной связи. При этом учитываются только совокупность событий, которая достаточна для логического порождения текущего состояния объекта.
Моделью подобной регистрации может служить формирование, в качестве состояния, множества A всех распознанных событий x с учетом момента i появления каждого из них и с отбрасыванием прежнего события при его повторении. Время T измеряется по старшему из зарегистрированных событий. Если распознана последовательность событий X=x(1),...,x(N) , то
A(N)={(x,i) | i=max{ j | x(j)=x; 1<= j<=N }, x in X };
T(N)=max{ N-i | (x,i) in A(N)} .
Если поток событий бернуллиевски стационарен с вероятностью f(x) для события x, то средний возраст события x до его замены на двойника в состоянии A равен 1/f(x) независимо от длительности наблюдений N.
Подобные шкалы, если пользоваться ими некритически, могут порождать иллюзии сжатия исторического времени. Дело в том, что реальная причина некоторых характеристик текущего состояния системы может заключаться не в последней подходящей для этого причине, а в том, что произошло раньше. Такие шкалы бывают прагматически удобными, если задачей является компактная запись текущего состояния путем логического сжатия информации. Например, ими пользуются при создании учебников, не ставящих задачей полный исторический обзор. Путь ученика к последним достижениям значительно короче пути предшественников. Но очень опасно принимать длину учебного курса за длину реально пройденного пути. Такие ошибки привели в последнее время к созданию спорных историографических концепций.
***
Сейчас значительно возрос научный интерес к эволюции самих математических теорий в реальном историческом времени. Здесь существенно учитывать как событийный поток математических открытий, так и логику эволюции эталонизированных (“строгих”) понятий, методов их введения в теорию и установления между ними взаимосвязей. История математики становится частью математики и, в какой-то мере, объектом ее исследования. Возможно, в будущем учебники будут предлагать несколько альтернативных введений математического объекта с разъяснением исторического смысла каждого варианта. Интересно, что в работах по искусственному интеллекту одним из эффективных методов стал режим совета человеку на основе ранее накопленного опыта в текстовой форме без использования собственно математической модели. Наверное, полезно было бы ввести и в математические учебники содержательные неформальные цитаты классиков науки, разъясняющие суть теории и причин ее возникновения, даже если формальный язык современной науки значительно отличается от начального. Необходим, также, анализ тупиковых направлений и существенных ошибок, преодоленных наукой. Таким образом время непосредственно войдет в математику.
12. Динамика математических приложений.
В этом разделе статьи будет рассмотрен процесс эталонизации знаний в нескольких областях науки. Будем считать, что эталонизация начинается с письменной регистрации фактов и знаний, хотя язык такой регистрации может быть далек от эталонности. Дело в том, что сама запись является эталонным объектом, а смысл ее может уточняться последующими записями.
За основу анализа динамики эталонизации науки примем ключевые этапы изменения ее информационной структуры. Автор сознает некоторую субъективность выбора этих этапов, однако эталонизация этого понятия в настоящее время видимо не возможна. В качестве компенсации на схемах предлагается подробный перечень этапов, что позволит читателю внести изменения по своему усмотрению.
На схемах 1, 2, 3 показаны распределения этапов эталонизации понятий для физики, биологии и информатики. Все эти схемы показывают ускорение процесса в двадцатом столетии, и его ступенчатый характер в прошлом. Характерна очень долгая фаза начальных описаний объектов науки, приходящаяся на период древнего Египта. Все диаграммы имеют стагнацию в период средних веков. Однако, это было время распространения в Европе достижений эллинского периода бурного развития науки, что и породило, в конечном счете, эпоху Возрождения и подготовило современный скачок. Обращает на себя внимание сравнительно длительный описательный период в биологии, сменившийся особенно крутым скачком в двадцатом столетии.
В целом, эти диаграммы показывают ступенчатый характер внедрения математики в приложения. За периодами бурного роста следуют длительные интервалы освоения достигнутого уровня.
На начальном этапе математизации реальные объекты используются для формирования логических понятий. В древнем мире так возникла геометрия и абстрактное понятие числа. В новое время — понятия графа, топологии, автомата и сетей. На более зрелом этапе в каждой науке начинается обратный процесс: математические понятия, полученные логическим анализом моделей, воспринимаются как новые реальные характеристики природных объектов (ускорение, энтропия, информация, энергия, импульс, кривизна пространства-времени, струны, калибровочный класс частиц и т. п.)
Крутые скачки диаграмм математизации связаны с созданием относительно изолированных научных центров на базе общественной поддержки. В древности так возникли школа Пифагора, финансируемая римским городом Рене, и неколько академий, поддерживаемых империей. В новое время скачок совпал с созданием систем учебных и исследовательских институтов, как государственных, так и на базе фирм.
Плотная серия новых этапов в эти периоды не означает замену ступенчатого развития на монотонное. Дело в том, что такие этапы, как правило, не последовательны в причинно-следственном смысле, а представляют собой параллельную серию прорывов в разных направлениях. Каждый такой прорыв порождает длительный период исследовательской работы, без новых этапных изменений.
Эта закономерность хорошо видна на примере открытия Архимедом десятичной записи чисел. Он использовал ее для доказательства отсутствия самого большого числа. Числа записывались камнями, лежащими в корзинах, которые были поставлены в ряд. Чтобы прибавить к числу единицу, надо было положить еще один камень в первую корзину. Если в ней оказывалось десять камней, корзина опрокидывалась, а один камень добавлялся в следующую корзину. Процесс опрокидывания и добавления продолжался до стабилизации. Если приходилось опрокидывать последнюю корзину, то добавлялась еще одна корзина, куда клали один камень. Таким образом от любого натурального числа можно было породить следующее, а роль нуля играла пустая корзина. Не смотря на очевидный прорыв, изобретения десятичной арифметики не последовало. Надо было догадаться еще до таблиц сложения и умножения. На это ушло в Европе более полутора тысяч лет. Идея родилась в Индии, возможно не без влияния европейской науки, связи с которой установились в период походов Александра Македонского, и вернулась в Европу через арабских ученых уже в эпоху раннего Возрождения.
Еще выразительнее стагнация двоичной системы исчисления. Ее открыл Пифагор в форме разложения любого числа по степеням двойки. Этот факт так поразил нумерологов, что ряд степеней двойки был объявлен священным. Однако создания двоичной арифметики (гораздо более простой, чем десятичная) за этим не последовало. Она была открыта только в девятнадцатом веке, как частный случай разложения чисел по произвольному основанию. Ее особая роль была осознана лишь в двадцатом столетии, когда выяснилось, что она обеспечивает наибольшую надежность автоматических вычислений. Столь большой период освоения открытия видимо связан с начальной мистической установкой нумерологии, где главной считалась религиозная суть числа, а вычисления были делом низменным и второстепенным.
Однако, система государственной поддержки в социумах, где наука носила жреческий характер, порождала длительную консервацию основных представлений и методов. Примером такой застывшей научно-религиозной системы может служить древний Египет или Вавилон. Достигнув на ранних этапах высокого уровня, они тысячелетиями потом поддерживали его, запрещая изменения. Иосиф Флавий цитирует египетского историка, рассказывающего об изгнании с позором жреца, пытавшегося ввести в храмовый обиход солнечные часы. Пифагор был вынужден бежать из Греции в зарождающуюся римскую империю под страхом смерти после попытки заниматься наукой в дельфийском храме. Его знания вернулись туда только век спустя с учениками, образовавшими Пифагорейское братство после разгрома школы (возможно, по политическим мотивам). Похожие явления можно было наблюдать при столкновении религиозных и научных интересов в эпоху Возрождения (инквизиция), и даже в новейшее время (изоляция Лобачевского за неклассические научные взгляды, изгнание Эйнштейна из Германии в период фашизма, борьба с генетикой и кибернетикой в сталинский период). Вероятно, прогресс требует еще и демократизации знаний, их прямой и эффективной связи с общественной практикой: ремеслами, хозяйствованием и политикой.
Этот анализ не затрагивает развития внутриматематических понятий и методов. Логика развития чистой математики несколько отлична от прикладных дисциплин. Однако, эталонная структура определений и вывода в полной мере присуща всей математике.
Литература.
1. А.В.Коганов. Метод расщепления истины в парадоксной защите логики. ХI международная конференция "Логика, методология, философия науки", т.2, с37.
2. А.В.Коганов. Анализ произведений искусства методом расщепления истины. "Математика и искусство" Труды конф., М. , 1997г., с 170-172
3. А. И. Мальцев. Алгоpитмы и pекуpсивные функции. "Наука", М.,1986, 367с.
4. Я. А. Силин. Совpеменная модальная логика. ЛГУ, Ленингpад, 1976, 104с.
5. Исследования по теоpии множеств и неклассическим логикам. Сб., "Наука", М., 1976г.,328с.
6. Иосиф Флавий. О древности иудейского народа. С-П., 1895г.

Схема 1.
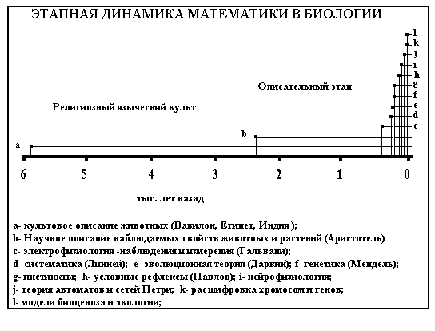
Схема 2.
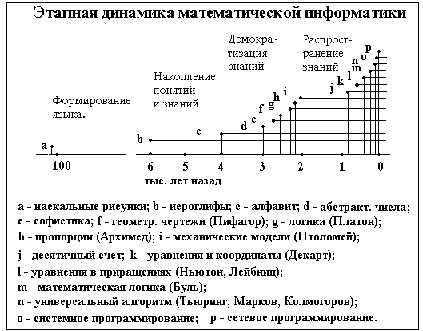
Схема 3.