Для феноменологического описания ранговых распределений (Левич, 1980) в экологии применяются различные аппроксимации: экспоненциальная модель , гиперболическоя модель , объединяющее их дзета-распределение ~, модель “разломанного стержня” ~ (в формулах обозначает численность особей ранга i; z, b и B — параметры моделей).

Вместо функций иногда анализируют их математические эквиваленты: распределения накопленных численностей (суммарную численность групп всех рангов от 1 до i), частотные распределения (число групп с численностями от n до n+Dn) или частотные распределения логарифмов численностей, функции экологической неаддитивности (зависимость числа групп в выборке от объема выборки).

Обнаружено (Левич, 1980), что в нормальном (ненарушенном, фоновом и т.п.) состоянии сообщества параметр рангового распределения заключен во вполне определенном диапазоне значений. Например, для численностей планктонных организмов в случае экспоненциальной модели z »  0,7 -0,9 или в случае гиперболической модели b  »  1,5 -2,5. (Напомню, что в лингвистике для “целостных” текстов выполняется b  = 1 (Zipf, 1949; Орлов, 1970).) Параметр рангового распределения специфичен для типа сообщества (например, для сообществ фитопланктона, зоопланктона или перифитона), для конкретной экосистемы, для сложившегося комплекса условий среды, к которым адаптировано сообщество. В той степени, в какой справедлив указанный закон, отклонения от него могут служить мерой патологии состояний сообщества. Другими словами, предлагается “градусник” для экосистем, где роль температуры играет параметр рангового распределения (замечу, что приведенная аналогия не является поверхностной метафорой, о чем пойдет речь в разделе о происхождении ранговых распределений).

Распространен метод диагностики, основанный на сравнении ранговых распределений численностей и биомасс одних и тех же групп организмов (Warwick, 1987). Этот АВС-метод (abundance-biomass comparison) основан на предположении о том, что в стабильных сообществах преобладают крупные виды с медленной динамикой, а в нарушенных — мелкие и более динамичные. Пользователи метода, как правило, предлагают свои способы расчета индексов отличия указанных распределений (Beukema, 1988; McManus and Paulv,1990; Meire and Deren, 1990; Аверинцев, 1991).

Существующие подходы. Известно несколько подходов к обоснованию формы ранговых распределений. Например, объяснение экспоненциального закона Мотомуры (Motomura, 1932) с помощью априорных представлений а различном “могуществе” видов при взаимодействии в сообществе. Беспараметрическая модель “разломанного стержня” МакАртура (MacArthur, 1960) рассчитывает результат случайного бросания точек на отрезок (“стержень”), олицетворяющий доступный сообществу запас единственного и равномерно распределенного ресурса. В.Д.Федоров (1978) в модели “экспоненциально разломанного стержня” делает то же на отрезке с экспоненциально распределенным ресурсом. Р.Кернер (Песенко, 1978) показал, что логнормальный закон следует из статистической механики системы “хищник-жертва”, описываемой уравнениями Вольтерра. Гиперболическую зависимость числа видов с данным значением существенного параметра от величины этого параметра выводят Б.Я.Рябко, Б.И.Кудрин, Н.Н.Завалишин и А.И.Кудрин (1978). Адекватную форму ранговых распределений для численностей биологических таксонов на основе модели самоподобных множеств выводят Ю.Г.Пузаченко и А.Ю.Пузаченко (1996).

Особое место в обосновании ранговых распределений занимают подходы, основанные на экстремальных принципах. Как правило, это вариации принципа максимума энтропии (Шрейдер, 1967; Мандельброт, 1973; Арапов, Шрейдер, 1977; Яблонский, 1986; Кудрин и др., 1987). Разработана модель (Левич, 1982; Левич и др., 1993; Левич и др., 1994; Levich, 1995), развивающая идеи экстремального подхода для обоснования распределений численности классов сложных открытых систем в условиях конкуренции за ресурсы. От существующих моделей ее отличают, в первую очередь, два обстоятельства. Первое из них — вывод, а не постулирование экстремизируемого функционала, и второе — учет ресурсных ограничений при условной оптимизации в виде неравенств, а не равенств, что в силу большей реалистичности и общности позволяет решать ряд задач, недоступных традиционному подходу.

где n_i — численность класса i; , w — число классов разбиения (например, видов в сообществе) и обозначает совокупность (n₁, n₂, ..., n_n). Если допустимы как размножение, смертность, так и слияние и интродукция особей, то инвариант структуры множеств с разбиениями в этом случае есть

Здесь m — число ресурсов, потребляемых системой; L^k — доступное системе количество ресурса k в среде (L^k >0);  — содержание (потребность) ресурса k в “особи” из класса i ; искомыми функциями являются численности классов n_i и их сумма n.

где величина n и множители Лагранжа l^k являются функциями ресурсов и отыскиваются из системы

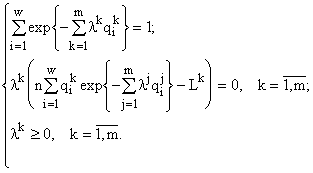
Обращу внимание на ряд особенностей модели. Рассматриваемые функционалы имеют “энтропиеобразный” вид. И это не случайно, так как и при вычислении больцмановской энтропии и при подсчетах инвариантов фактически рассчитывается одна и на же величина — логарифм количества допустимых микросостояний (допустимых преобразований), соответствующих заданному макросостоянию (структуре) системы. Таким образом, инварианты могут рассматриваться как “обобщенные энтропии” математических структур. Существенно, что эти “энтропии” точно рассчитываются вне каких-либо статистических представлений и для любых, сколь угодно малых или больших численностей n_i. Многие их полученных инвариантов известны в экологии как императивные (в отличие от параметрических — параметров ранговых распределений) индексы разнообразия. Так, например, приведенные выше инварианты соответствуют индексам МакАртура (MacArthur, 1955) и Симпсона (Simpson, 1949).

- наименьшее количество допустимых структурой системы преобразований (т.е. наибольшая устойчивость) при максимальной экспансии системы (росте тотальной численности n);

Формула видовой структуры и ранговые распределения. В формуле видовой структуры номер i маркирует классы сообщества и не обязательно соответствует рангу класса по численности. Предположим, что маркировка выбрана в соответствии с рангами, тогда формула видовой структуры превращается в ранговое распределение численностей.

Пусть m = 1, т.е. потребляется единственный ресурс. Пусть потребности видов в этом ресурсе распределены линейно: -q_i º  q₁i. Тогда формула видовой структуры задает экспоненциальное ранговое распределение n_i/n = zⁱ, где z = e^-lq1. Пусть потребности видов распределены по закону q_i = q₀ ln(B +i), тогда n_i/n ~ 1/(B +i)^b, где b=lq₀. Для такого медленноменяющегося распределения потребностей, как q_i ~ lnlni, получаем распределение численностей, близкое к задаваемому моделью “разломанного стержня” распределению n_i ~ lni. В случае двух ресурсов и распределений потребностей и получаем двухпараметрическое дзета-распределение численностей. Становится понятной резко убывающая форма ранговых распределений: согласно формуле видовой структуры, численности экспоненциально зависят от монотонных распределений потребностей. Таким образом, распределение численностей полностью порождается распределением их потребностей. Параметры ранговых распределений пропорциональны множителям Лагранжа соответствующей вариационной задачи. (Замечу, что в задачах статистической физики принцип максимума энтропии использовали неоднократно (Больцман, 1953; Gibbs, 1902, Jaynes, 1957; Haken, 1988). При рассмотрении газа и ограничений по энергии величина 1/l интерпретируется как температура газа T.)

В качестве спекулятивной иллюстрации приведу доводы в пользу ципфовской модели рангового распределения встречаемости слов в текстах. Пусть i обозначает ранг встречаемости некоторого слова в текстах, по которым происходит обучение индивидуума языку. Введем понятие “усилия l(i) по воспроизведению слова i“ при создании текстов. Согласно физиологическому закону Фехнера величины стимула и реакции связаны логарифмической зависимостью. Поэтому “потребность“ q_i слова i в усилии по его воспроизведению при создании текста можно считать пропорциональной log i, и, следовательно, встречаемость этого слова в тексте и его ранг окажутся связанными гиперболической зависимостью.

Теорема стратификации (Левич и др., 1994). Пространство ресурсов среды разбивается (стратифицируется) на 2^m -1 непересекающихся областей S^J , в каждом из которых:

- ресурсы kÎ J и только они потребляются полностью (неравенства вариационной задачи превращаются в строгие равенства, а для ресурсов kÏ J неравенства обращаются в строгие неравенства);

- численности n_i (через параметры n и из формулы видовой структуры) зависят только от величин L^k для ресурсов kÎ J.

Теорема стратификации позволяет по заданным наборам определить, в каком страте лежит заданный вектор ресурсов , т.е. какие ресурсы фактически определяют (лимитируют) функционирование сообщества.

Теорема оптимизации (Левич и др., 1993). Относительные численности классов n_i/n зависят только от отношений L^k/L^j лимитирующих ресурсов; эти численности достигают максимальной величины при отношениях ресурсов, равных отношениям соответствующих потребностей. Теорема оптимизации задает путь управления (стимулирования или подавления) видовыми обилиями n_i/n с помощью отношений лимитирующих ресурсов в среде.

Теорема Гиббса (Левич и Алексеев, 1996). Для любого ресурса j рассмотренная вариационная задача на максимум энтропии при ограничениях сверху на потребленные ресурсы эквивалентна следующей вариационной задаче:

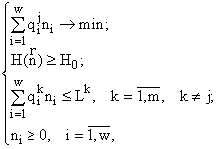
где H₀ — некоторая константа (однозначно связанная с параметрами исходной задачи). Роль теоремы Гиббса для интерпретации экстремального принципа уже отмечалась.

- вектор имеющихся в распоряжении системы ресурсов, подчиняющихся законам сохранения (т.е. не информационных, не поведенческих, не моральных и т.д.);

- вектора потребностей объектов класса i в ресурсах . Потребности –системообразующий фактор, т.е. в класс i объединяются все потребители с одинаковыми потребностями . Некоторые из могут быть нулевыми.

Пусть необходимо отыскать численности классов , i =. (Номер i лишь маркирует класс, т.е. порядок номеров не существенен.)

- выявление ресурсов, ограничивающих функционирование системы, т.е. отыскание подмножества ресурсов такого, что ресурсы потребляются системой полностью и добавление их в систему приводит к росту численностей .

- расчет функций .

- расчет парциальных потреблений, лимитирующих ресурсов каждым классом i системы .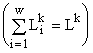

- расчет реальных потреблений и (всей системой и каждым ее классом) ресурсов, не являющихся лимитирующими (эти ресурсы не потребляются из среды полностью), другими словами, расчет сценариев сбалансированного потребления ресурсов.

- оптимизация численностей классов , т.е. расчет комбинации параметров задачи , при которых численность максимальна или минимальна. Другими словами, указание пути управления “видовой” структурной системы.

- расчет интегральных характеристик системы: ранговых распределений n(j); индексов разнообразия системы и др.

- оценка состояния системы в терминах нормы и патологии с помощью интегральных характеристик. Расчеты допустимых уровней воздействий, нарушающих нормальное функционирование системы.