Категорно-функторное моделирование естественных систем
А.П.Левич, А.В.Соловьев
1. Введение
Теоретическое описание любой естественной системы должно включать в себя по крайней мере два важных аспекта. Во-первых, построение конкретной математической модели допустимых состояний системы и ее переходов между этими состояниями. Во-вторых, установление правил отбора (часто в форме экстремального принципа), позволяющих находить среди множества теоретически допустимых состояний системы те, которые осуществляются в реальности при данных внешних условиях. В настоящей статье обе указанные задачи предлагается решать при помощи методов теории категорий.
По-видимому, первым, кто в полной мере использовал средства теории множеств и топологии для моделирования биологических процессов, был Н.Рашевский, заложивший основы “абстрактной биологии” [1-4]. Затем Р.Розен в своих работах по реляционной биологии [5-7] применил теорию категорий с целью математического описания биологических систем и, в частности, живой клетки. Абстрактный категорно-функторный подход к задачам теоретической биологии разрабатывался в последующие годы в нескольких направлениях, среди которых прежде всего отметим теорию молекулярных множеств А.Бартоломея [8,9], теорию организмических суперкатегорий И.Баяну [10,11] и энергетическую теорию абстрактных экологических систем К.Легизамона [12,13].
В данной работе предпринята попытка построения категорно-функторной модели абстрактных естественных систем (необязательно биологических) и рассмотрено ее приложение к описанию экологических сообществ. Статья содержит развитие идей, изложенных в книге [14].
2. Теоретико-категорная модель естественных систем
Как показывает анализ, во всех практически интересных случаях произвольное состояние, а часто и пространство состояний естественной системы, удается отождествить с некоторым множеством, наделенным определенной математической структурой (алгебраической, топологической и т.д.).
Например, состояние экологического сообщества удобно описывать множеством с разбиением на непересекающиеся классы [14], где элементами множества являются организмы, образующие данное сообщество, а классами разбиения — популяции биологических видов. В дальнейшем основные положения общей теории будем иллюстрировать на примере экологического сообшества.
Возвращаясь к произвольной естественной системе, отметим, что математическая структура, заданная на множествах-состояниях, моделирует лишь те свойства реальной системы, которые сохраняются неизменными при ее переходах из одного допустимого состояния в любое другое. Именно таким свойством является наличие видовой структуры у экологического сообщества. Таким образом, в общем случае пространство состояний естественной системы представляет собой класс одинаково структурированных множеств (это могут быть группы, топологические пространства, множества с разбиениями и т.п.).
Пусть A и B — одинаково структурированные множества. Напомним, что соответствием c из A в B называется подмножество c Ì
A´
B. При этом используются обозначения: c(a)º
{
b|
(a,b)Î
c}
Ì
B для полного образа элемента aÎ
A по соответствию c и c![]() (b)º
{
a|
(a,b)Î
c}
Ì
A для полного прообраза элемента bÎ
B по соответствию c. Возможны ситуации, когда c(a)=Æ
и c
(b)º
{
a|
(a,b)Î
c}
Ì
A для полного прообраза элемента bÎ
B по соответствию c. Возможны ситуации, когда c(a)=Æ
и c![]() (b)=Æ
при некоторых a и b. Перечислим наиболее важные типы соответствий из A в B:
(b)=Æ
при некоторых a и b. Перечислим наиболее важные типы соответствий из A в B:
1) Всюду определенное соответствие pÌ A´ B, для которого p(a)¹ Æ при любом aÎ A;
2) Сюръективное соответствие sÌ
A´
B, для которого s![]() (b)¹
Æ
при любом bÎ
B.
(b)¹
Æ
при любом bÎ
B.
3) Функциональное соответствие fÌ A´ B, для которого f(a) либо пусто, либо состоит из одного элемента при любом aÎ A;
4) Инъективное соответствие iÌ
A´
B, для которого i![]() (b) либо пусто, либо состоит из одного элемента при любом bÎ
B.
(b) либо пусто, либо состоит из одного элемента при любом bÎ
B.
Кроме того, допустимы различные комбинации типов 1-4; в частности, всюду определенные и одновременно функциональные соответствия, которые будем отождествлять с обычными отображениями. Все они понадобятся в дальнейшем.
Соответствия, сохраняющие математическую структуру, заданную на множествах A и B, будем называть морфизмами структуры и обозначать греческими буквами: a , b , g ,... [14]. Например, морфизмами структуры множеств с разбиениями являются соответствия, переводящие каждый класс разбиения одного множества целиком в некоторый класс разбиения другого множества так, что разные классы преобразуются в разные. Другими примерами морфизмов структуры являются гомоморфизмы групп и непрерывные отображения топологических пространств.
На основании сказанного выше переходы между допустимыми состояниями произвольной естественной системы будем отождествлять с морфизмами соответствующей математической структуры. Ясно, что каждая система характеризуется вполне определенным, присущим только ей, классом морфизмов. Даже если системы имеют одно и то же пространство состояний, но характеризующие их классы морфизмов не совпадают, то такие системы следует различать.
Таким образом, со всякой естественой системой предлагается связать математическую конструкцию S, состоящую из двух классов: ObS и MorS. Здесь ObS — фиксированный класс одинаково структурированных множеств, которые будем также называть объектами; MorS — фиксированный класс морфизмов структуры, заданной на этих множествах. Нетрудно видеть, что:
1) Каждой упорядоченной паре объектов (A,B)Î ObS´ ObS отвечает множество MorS(A,B)Ì MorS морфизмов структуры из A в B. Не исключается случай, когда MorS (A,B)=Æ для некоторых A и B.
2) Каждый морфизм из класса MorS принадлежит одному и только одному множеству Mor S (A,B), где A,BÎ ObS.
3) Для каждой тройки объектов A,B,CÎ ObS в классе MorS естественным образом вводится операция умножения морфизмов: MorS(A,B)´ MorS(B,C)® MorS(A,C),(a ,b )® a b . Здесь a b Î MorS (A,C) — композиция морфизмов a Î MorS(A,B) и b Î MorS(B,C), определяемая следующими условиями: (a,c)Î a b при aÎ A и cÎ C тогда и только тогда, когда существует элемент bÎ B такой, что одновременно (a,b)Î a и (b,c)Î b .
4). Умножение морфизмов ассоциативно, т.е. (a b )g =a (b g ) для любых a Î MorS(A,B), b Î MorS(B,С), g Î MorS(С,D).
5). Для каждого AÎ ObS существует морфизм 1AÎ MorS(A,A), называемый единичным, такой, что 1Aa =a и b 1A=b при любых a Î MorS(A,B), b Î MorS(С,A) и C,BÎ ObS. Это тождественное соответствие: 1A ={ a,a)| aÎ A} Ì A´ A.
Следовательно, S является категорией [16,17]. Таким образом, предлагаемая модель естественных систем допускает простую теоретико-категорную интерпретацию, согласно которой допустимые состояния системы представляют собой объекты категории S, а разрешенные переходы между этими состояниями — морфизмы категории S.
3. Функторный метод сравнения структурированных множеств и экстремальный принцип для естественных систем
Следующий важный шаг при описании естественной системы состоит в установлении экстремального принципа, позволяющего выделять из совокупности допустимых лишь те состояния, которые реализуются в заданных внешних условиях. Для этого необходимо построить функцию на пространстве состояний системы со значениями в некотором линейно упорядоченном множестве, ибо только тогда осмыслено само понятие “экстремальное состояние”. В настоящем разделе займемся поиском такой функции, определенной на классе ObS и имеющей наиболее естественный с точки зрения теории категорий вид.
Прежде всего напомним некоторые сведения о кардинальных числах неструктурированных множеств. Рассмотрим категорию Set, объектами которой являются произвольные множества, а морфизмами — произвольные соответствия между этими множествами. Бинарными отношениями на классе ObSet условимся называть подклассы прямого произведения ObSet´ ObSet.
Пусть R![]() — бинарное отношение на ObSet, определяемое правилом: (A,B)Î
R
— бинарное отношение на ObSet, определяемое правилом: (A,B)Î
R![]() Û
существует инъективное отображение из A в B. Очевидно, R
Û
существует инъективное отображение из A в B. Очевидно, R![]() обладает следующими свойствами:
обладает следующими свойствами:
1) (A,A)Î
R![]() для любого AÎ
ObSet (рефлексивность);
для любого AÎ
ObSet (рефлексивность);
2) Если (A,B)Î
R![]() и (B,C)Î
R
и (B,C)Î
R![]() , то (A,C)Î
R
, то (A,C)Î
R![]() (транзитивность),
(транзитивность),
т.е. оно является отношением предпорядка на ObSet. Факторизуем предпорядок R![]() путем введения на том же классе ObSet бинарного отношения E
путем введения на том же классе ObSet бинарного отношения E![]() согласно правилу: (A,B)Î
E
согласно правилу: (A,B)Î
E![]() Û
(A,B)Î
R
Û
(A,B)Î
R![]() и (B,A)Î
R
и (B,A)Î
R![]() . Нетрудно убедиться, что так определенное отношение E
. Нетрудно убедиться, что так определенное отношение E![]() рефлексивно, транзитивно и симметрично (последнее означает, что если (A,B)Î
E
рефлексивно, транзитивно и симметрично (последнее означает, что если (A,B)Î
E![]() то и (B,A)Î
E
то и (B,A)Î
E![]() ). Следовательно, E
). Следовательно, E![]() есть отношение эквивалентности на ObSet. Можно показать, что (A,B)Î
E
есть отношение эквивалентности на ObSet. Можно показать, что (A,B)Î
E![]() тогда и только тогда, когда существует биекция между A и B [15].
тогда и только тогда, когда существует биекция между A и B [15].
Для каждого AÎ
ObSet символом [A]![]()
![]() обозначим класс всех множеств, E
обозначим класс всех множеств, E![]() -эквивалентных множеству A, т.е. положим
-эквивалентных множеству A, т.е. положим
[A]![]() ={
A’|
(A,A’)Î
E1}
Ì
ObSet. Этот класс обычно называют кардинальным числом множества A и пишут CardA=[A]
={
A’|
(A,A’)Î
E1}
Ì
ObSet. Этот класс обычно называют кардинальным числом множества A и пишут CardA=[A]![]()
![]() (если A — конечное множество, то CardA называют количеством элементов в A). Иными словами, кардинальные числа неструктурированных множеств являются элементами факторкласса ObSet/E
(если A — конечное множество, то CardA называют количеством элементов в A). Иными словами, кардинальные числа неструктурированных множеств являются элементами факторкласса ObSet/E![]() . Имеем одновременно каноническую сюръекцию CardA:ObSet®
ObSet/E1, A®
CardA.
. Имеем одновременно каноническую сюръекцию CardA:ObSet®
ObSet/E1, A®
CardA.![]()
![]()
На факторклассе ObSet/E1 естественным образом определяется отношением порядка. Именно: CardA£
1CardBÛ
(A,B)Î
R1. Рефлексивность и транзитивность “£
1” следуют из соответствующих свойств предпорядка R![]() . Антисимметричность “£
1” устанавливается простым рассуждением: CardA£
1CardB и CardB£
1CardAÛ
(A,B)Î
R1 и (B,A)Î
R1Û
(A,B)Î
E1Þ
CardA=[A]
. Антисимметричность “£
1” устанавливается простым рассуждением: CardA£
1CardB и CardB£
1CardAÛ
(A,B)Î
R1 и (B,A)Î
R1Û
(A,B)Î
E1Þ
CardA=[A]![]() =[B]
=[B]![]() =CardB. Таким образом, отношение “£
=CardB. Таким образом, отношение “£
![]() ” действительно является отношением порядка на ObSet/E
” действительно является отношением порядка на ObSet/E![]() , причем этот порядок оказывается линейным (всякие два кардинальных числа сравнимы) [15].
, причем этот порядок оказывается линейным (всякие два кардинальных числа сравнимы) [15].
Распространим теперь описанную выше схему рассуждений на случай категории S одинаково структурированных множеств. Пусть A,BÎ ObS. По аналогии с общей алгеброй, инъективные отображения из A в B (и из B в A), сохраняющие математическую структуру, заданную на этих множествах, будем называть мономорфизмами структуры.
Рассмотрим бинарное отношение R![]() на классе ObS, определяемое следующим правилом: (A,B)Î
R
на классе ObS, определяемое следующим правилом: (A,B)Î
R![]() Û
существует мономорфизм структуры из A в B. Очевидно, отношение R
Û
существует мономорфизм структуры из A в B. Очевидно, отношение R![]() рефлексивно и транзитивно, т.е. является предпорядком на ObS. Факторизация предпорядка R
рефлексивно и транзитивно, т.е. является предпорядком на ObS. Факторизация предпорядка R![]() стандартным образом порождает отношение эквивалентности E
стандартным образом порождает отношение эквивалентности E![]() на том же классе ObS: :(A,B)Î
E
на том же классе ObS: :(A,B)Î
E![]() Û
(A,B)Î
R
Û
(A,B)Î
R![]() и (B,A)Î
R
и (B,A)Î
R![]() .
.
Для каждого AÎ
ObS введем класс [A]![]() ={A’|
(A,A’)Î
E
={A’|
(A,A’)Î
E![]() }Ì
ObS одинаково структурированных множеств, E
}Ì
ObS одинаково структурированных множеств, E![]() -эквивалентных множеству A. Следуя [14], назовем этот класс структурным числом множества A и используем для него обозначение: StrA=[A]
-эквивалентных множеству A. Следуя [14], назовем этот класс структурным числом множества A и используем для него обозначение: StrA=[A]![]() . Таким образом, структурные числа по определению являются элементами факторкласса ObS/E
. Таким образом, структурные числа по определению являются элементами факторкласса ObS/E![]() . Имеем одновременно каноническую сюръекцию Str:ObS®
ObS/E
. Имеем одновременно каноническую сюръекцию Str:ObS®
ObS/E![]() , A®
StrA.
, A®
StrA.
С помощью R![]() зададим на факторклассе ObS/E
зададим на факторклассе ObS/E![]() отношение порядка, полагая: StrA£
отношение порядка, полагая: StrA£
![]() StrBÛ
(A,B)Î
R
StrBÛ
(A,B)Î
R![]() . Элементарно проверяются рефлексивность, транзитивность и антисимметричность так определенного отношения “£
. Элементарно проверяются рефлексивность, транзитивность и антисимметричность так определенного отношения “£
![]() ”. Однако, в отличие от кардинальных, структурные числа упорядочены, вообще говоря, лишь частично. Например, для множеств с разбиениями A = {{
a,b}
{
c,d,e}
} и B = {{
a}
{
b,c,d,e}
} не существует мономорфизмов ни из A в B, ни из B в A, т.е. соответствующие структурные числа StrA и StrB оказываются несравнимыми. Таким образом, никакая функция на ObS, принимающая значения в факторклассе ObS/E
”. Однако, в отличие от кардинальных, структурные числа упорядочены, вообще говоря, лишь частично. Например, для множеств с разбиениями A = {{
a,b}
{
c,d,e}
} и B = {{
a}
{
b,c,d,e}
} не существует мономорфизмов ни из A в B, ни из B в A, т.е. соответствующие структурные числа StrA и StrB оказываются несравнимыми. Таким образом, никакая функция на ObS, принимающая значения в факторклассе ObS/E![]() , ввиду частичной упорядоченности последнего не может служить удовлетворительной основой для экстремального принципа.
, ввиду частичной упорядоченности последнего не может служить удовлетворительной основой для экстремального принципа.
Выход из создавшегося положения будем искать на пути построения представления структурных чисел более удобной для наших целей струкутрой порядка. Для этого используем тот факт, что S является категорией и что факторкласс ObSet/E![]() категории Set линейно упорядочен.
категории Set линейно упорядочен.
Фиксируем в классе ObS произвольный объект A. Рассмотрим отображение FA:S® Set, сопоставляющее каждому BÎ ObS множествоFA(B) = MorS(A,B)Î ObSet морфизмов структуры из A в B и каждому b Î MorS (B,C)Ì MorS — всюду определенное и функциональное соответствие FA(b )={ (a ,a b )| a Î MorS(A,B)} Ì Ì MorS (A,B)´ MorS(A,C) из FA (B) в FA (С) при любых B,CÎ ObS. Очевидно, выполняются следующие условия:
1). Если BÎ ObS, то FA (B)Î ObSet;
2). Если b Î MorS(B,C), то FA (b )Î MorSet (FA(B), FA (С));
3). FA (1B)= 1![]() для любого BÎ
ObS;
для любого BÎ
ObS;
4). Если b
Î
Mor S ( B,C) и![]() g
Î
Mor S (C,D), то FA (b
g
)=FA (b
) FA (g
).
g
Î
Mor S (C,D), то FA (b
g
)=FA (b
) FA (g
).
Значит, отображение FA является одноместным ковариантным функтором из категории S в категорию Set [16], известное как представляющий функтор.
Следуя [14], назовем кардинальное число JA(B) º
Card MorS(A,B)= =Card FA(B) инвариантом объекта BÎ
ObS относительно объекта AÎ
ObS. При фиксированном A имеем функцию J A:ObS ®
ObSet/E![]() , B®
JA (B). Она, как нетрудно видеть, представляет собой композицию инъекции F
, B®
JA (B). Она, как нетрудно видеть, представляет собой композицию инъекции F![]() :ObS®
ObSet, B®
FA(B) и канонической сюръекции Card:ObSet®
ObSet/E1. Более того, справедливо следующее утверждение: если StrB £
:ObS®
ObSet, B®
FA(B) и канонической сюръекции Card:ObSet®
ObSet/E1. Более того, справедливо следующее утверждение: если StrB £
![]() StrC, то JA (B)£
StrC, то JA (B)£
![]() J A (C). Действительно, условие StrB £
2StrC означает, то существует мономорфизм структуры из B в C. Пусть b
Î
MorS (B,C) такой мономорфизм и пусть a
,a
‘Î
MorS (A,B) — произвольные морфизмы. Поскольку b
является всюду определенным, функциональным и инъективным соответствием, равенство a
b
=a
‘b
влечет за собой a
=a
‘. Следовательно, FA(b
)Î
MorSet (FA (B), FA (C)) — инъекция и JA (B) £
J A (C). Действительно, условие StrB £
2StrC означает, то существует мономорфизм структуры из B в C. Пусть b
Î
MorS (B,C) такой мономорфизм и пусть a
,a
‘Î
MorS (A,B) — произвольные морфизмы. Поскольку b
является всюду определенным, функциональным и инъективным соответствием, равенство a
b
=a
‘b
влечет за собой a
=a
‘. Следовательно, FA(b
)Î
MorSet (FA (B), FA (C)) — инъекция и JA (B) £
![]() JA (С). В частности, если StrB=StrC, то JA(B)=JA(С). Именно в этом смысле следует понимать введенный выше для JA(B)Î
ObSet/E
JA (С). В частности, если StrB=StrC, то JA(B)=JA(С). Именно в этом смысле следует понимать введенный выше для JA(B)Î
ObSet/E![]() термин “инвариант”. Поскольку факторкласс ObSet/E
термин “инвариант”. Поскольку факторкласс ObSet/E![]() линейно упорядочен, для любых A,B,CÎ
ObS имеем: JA(B) £
линейно упорядочен, для любых A,B,CÎ
ObS имеем: JA(B) £
![]() JA(С), либо JA(С) £
JA(С), либо JA(С) £
![]() JA(B), либо JA(B)=JA(С). Таким образом, объекты категории S предлагается сравнивать между собой путем сравнения их инвариантов. Данное обстоятельство составляет сущность функторного метода сравнения структурированных множеств [14].
JA(B), либо JA(B)=JA(С). Таким образом, объекты категории S предлагается сравнивать между собой путем сравнения их инвариантов. Данное обстоятельство составляет сущность функторного метода сравнения структурированных множеств [14].
Функция JA определена на всем ObS и принимает значения в линейно упорядоченном факторклассе ObSet/E![]() , т.е. она вполне может быть использована в экстремальном принципе. Имея в виду дальнейшие приложения к ограниченным естественным системам, начиная с этого момента, сосредоточим свое внимание на конечных множествах.
, т.е. она вполне может быть использована в экстремальном принципе. Имея в виду дальнейшие приложения к ограниченным естественным системам, начиная с этого момента, сосредоточим свое внимание на конечных множествах.
В качестве S рассмотрим категорию Finseta, объектами которой являются любые конечные неструктурированные множества, а морфизмами — все соттветствия между ними, обладающие свойством “a” (мультииндекс a принимает одно из 16-ти значений, являющихся подмножествами множества {
p,s,f,i}
основных типов соответствий, перечисленных в разделе 2. Предположим, что A,BÎ
ObFinseta и CardA=m, CardB=n, где m,n — натуральные числа. Символом J![]() (B) обозначим инвариант объекта B относительно объекта A в категории FinsetA. Очевидно, J
(B) обозначим инвариант объекта B относительно объекта A в категории FinsetA. Очевидно, J![]() (B) совпадает с количеством морфизмов из A в B и является функцией от m и n. Ниже приводятся результаты вычисления инвариантов для всех 16 значений мультииндекса a.
(B) совпадает с количеством морфизмов из A в B и является функцией от m и n. Ниже приводятся результаты вычисления инвариантов для всех 16 значений мультииндекса a.
1) J![]() (B)=(2n–1)m; 2) J
(B)=(2n–1)m; 2) J![]() (B)=(2m–1)n ; 3) J
(B)=(2m–1)n ; 3) J![]() (B)=(n+1)m;
(B)=(n+1)m;
4) J![]() (B)=(m+1)n; 5) J
(B)=(m+1)n; 5) J![]() (B)=
(B)=![]() (PB); 6) J
(PB); 6) J![]() (B)=nm ;
(B)=nm ;
7) J![]() (B)=
(B)= ![]() J
J![]() (Ck); 8) J
(Ck); 8) J![]() (B)=
(B)= ![]() J
J![]() (Ck);
(Ck);
9) J![]() (B)=mn; 10) J
(B)=mn; 10) J![]() (B)=
(B)= ![]()
![]() k!;
k!;
11) J![]() (B)=
(B)= ![]() (–1)k (n–k)m;
(–1)k (n–k)m;
12) J![]() (B)=
(B)= ![]() (–1)k (m–k)n; 13) J
(–1)k (m–k)n; 13) J![]() (B)=
(B)=![]() ;
;
14) J![]() (B)=
(B)=![]() ; 15) J
; 15) J![]() (B)=m!; 16) JA (B)=2mn ,
(B)=m!; 16) JA (B)=2mn ,
где TB — система всех покрытий множества B, ![]() º
º
![]() , а Ck — произвольное k-элементное множество.
, а Ck — произвольное k-элементное множество.
Рассмотрим теперь в качестве S категорию FSa такую, что класс ObFSa состоит из конечных одинаково структурированных множеств, а класс MorFSa — из морфизмов структуры, обладающих одним из 16-ти свойств соответствий, обозначенных выше мультииндексом “a”. Категория FSa уже предоставляет достаточно средств для моделирования широкого спектра естественных систем.
Пусть A,BÎ
ObFSa и J![]() (B) — инвариант объекта B относительно объекта A в категории FSa, т.е. J
(B) — инвариант объекта B относительно объекта A в категории FSa, т.е. J![]() (B)=CardMor
(B)=CardMor![]() (A,B). (Например, если FSa — категория конечных множеств с разбиениями, то J
(A,B). (Например, если FSa — категория конечных множеств с разбиениями, то J![]() (B)=
(B)=![]() (kt(i)), где k i — i-ый класс разбиения множества A, kt(i) — класс разбиения множества B, в который переходит класс k i под воздействием морфизмов из Mor
(kt(i)), где k i — i-ый класс разбиения множества A, kt(i) — класс разбиения множества B, в который переходит класс k i под воздействием морфизмов из Mor![]() (A,B) [14].) Пусть, кроме того, A’,B’Î
ObFinseta — те же самые множества A и B, но только лишенные заданной на них математической структуры (так называемые носители структуры). Рассмотрим величину J
(A,B) [14].) Пусть, кроме того, A’,B’Î
ObFinseta — те же самые множества A и B, но только лишенные заданной на них математической структуры (так называемые носители структуры). Рассмотрим величину J![]() (B’)/J
(B’)/J![]() (B), называемую удельным инвариантом BÎ
ObFSa относительно AÎ
ObFSa. Удельный инвариант удобно выбрать за числовую меру удаленности структурированных множеств A и B от соответствующих носителей A’ и B’ математической структуры. Применительно к естественным системам это означает, что состояния системы с бó
льшими значениями удельного инварианта сильнее “структурированы”, нежели состояния с меньшими значениями последнего. Сказанное делает целесообразным введение следующего определения:
(B), называемую удельным инвариантом BÎ
ObFSa относительно AÎ
ObFSa. Удельный инвариант удобно выбрать за числовую меру удаленности структурированных множеств A и B от соответствующих носителей A’ и B’ математической структуры. Применительно к естественным системам это означает, что состояния системы с бó
льшими значениями удельного инварианта сильнее “структурированы”, нежели состояния с меньшими значениями последнего. Сказанное делает целесообразным введение следующего определения:
Энтропией H![]() (B) состояния BÎ
ObFSa относительно состояния AÎ
ObFSa естественной системы назовем логарифм соответствующего удельного инварианта, т.е. H
(B) состояния BÎ
ObFSa относительно состояния AÎ
ObFSa естественной системы назовем логарифм соответствующего удельного инварианта, т.е. H![]() (B)=ln
(B)=ln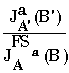 . При фиксированном A энтропия H
. При фиксированном A энтропия H![]() (B), очевидно, является функцией от BÎ
ObFSa со значениями в полупрямой [0,+¥
). Если классы состояний, между которыми допустимы переходы с точки зрения каких-либо содержательных соображений, например, в силу сохранения макропараметров системы, интерпретировать как макросостояние системы, а результат произвольного преобразования системы интерпретировать как ее микросостояние, то величину H
(B), очевидно, является функцией от BÎ
ObFSa со значениями в полупрямой [0,+¥
). Если классы состояний, между которыми допустимы переходы с точки зрения каких-либо содержательных соображений, например, в силу сохранения макропараметров системы, интерпретировать как макросостояние системы, а результат произвольного преобразования системы интерпретировать как ее микросостояние, то величину H![]() (B) можно считать обобщением больцмановской энтропии, определяемой обычно как логарифм удельного числа различающихся микросостояний, соответствующих ее макросостоянию. Возможность указанной интерпретации и совпадение частных случаев величины H
(B) можно считать обобщением больцмановской энтропии, определяемой обычно как логарифм удельного числа различающихся микросостояний, соответствующих ее макросостоянию. Возможность указанной интерпретации и совпадение частных случаев величины H![]() (B) с традиционными формулами для больцмановской энтропии послужили основанием для использования термина “энтропия”. Заметим, что в предложенном контексте энтропия появляется вне каких-либо вероятностных соображений.
(B) с традиционными формулами для больцмановской энтропии послужили основанием для использования термина “энтропия”. Заметим, что в предложенном контексте энтропия появляется вне каких-либо вероятностных соображений.
Теперь уже ясно, как сформулировать экстремальный принцип, управляющий поведением исследуемой естественной системы. Именно, предлагается принять следующий постулат:
из заданного состояния AÎ
ObFSa системы в реальности осуществляется переход в то состояние BÎ
ObFSa, для которого энтропия H![]() (B) максимальна в пределах, допускаемых внешними условиями (например, имеющимися энергетическими и другими ресурсами).
(B) максимальна в пределах, допускаемых внешними условиями (например, имеющимися энергетическими и другими ресурсами).
Сформулированный экстремальный принцип допускает различные интерпретации:
1) По определению удельный инвариант J![]() (B’)/J
(B’)/J![]() (B) (при фиксированном A) рассматривается как мера удаленности структурированного множества BÎ
ObFSa от носителя структуры B’Î
ObFinseta. Таким образом, согласно экстремальному принципу предпочтительными являются состояния {
B}
естественной системы, которые сильнее других удалены от своих полностью бесструктурных аналогов {
B’}
, т.е. максимально “структурированы”.
(B) (при фиксированном A) рассматривается как мера удаленности структурированного множества BÎ
ObFSa от носителя структуры B’Î
ObFinseta. Таким образом, согласно экстремальному принципу предпочтительными являются состояния {
B}
естественной системы, которые сильнее других удалены от своих полностью бесструктурных аналогов {
B’}
, т.е. максимально “структурированы”.
2) Инвариант J![]() (B’) при фиксированном A’ зависит лишь от количества элементов в множестве B’. Поэтому, если CardB’ фиксировано, то энтропия H
(B’) при фиксированном A’ зависит лишь от количества элементов в множестве B’. Поэтому, если CardB’ фиксировано, то энтропия H![]() (B) максимальна, когда инвариант J
(B) максимальна, когда инвариант J![]() (B) минимален. Но малое число морфизмов структуры из A в B можно трактовать как высокую “устойчивость” состояния B. Экстремальный принцип тогда реализует состояния как с максимальным числом элементов в множестве-носителе математической структуры, так и с максимальной “устойчивостью” по отношению к морфизмам структуры.
(B) минимален. Но малое число морфизмов структуры из A в B можно трактовать как высокую “устойчивость” состояния B. Экстремальный принцип тогда реализует состояния как с максимальным числом элементов в множестве-носителе математической структуры, так и с максимальной “устойчивостью” по отношению к морфизмам структуры.
3) Энтропию H![]() (B) можно рассматривать как количество информации, связанной со структурой состояний системы [18]. Поэтому экстремальный принцип можно интерпретировать и в информационных терминах: осуществляется состояние с максимальным количеством информации.
(B) можно рассматривать как количество информации, связанной со структурой состояний системы [18]. Поэтому экстремальный принцип можно интерпретировать и в информационных терминах: осуществляется состояние с максимальным количеством информации.
4. Применение экстремального принципа в экологии сообществ
Рассмотрим экологическое сообщество, состоящее из организмов одного трофического уровня без возрастной структуры (например, из клеток фитопланктона), принадлежащих w видам и потребляющих m взаимонезаменимых ресурсов. Предположим, что в данном сообществе допустимы деление клеток и их гибель, но недопустимы поглощение одних организмов другими и интродукция особей извне. Поскольку состояния экологического сообщества трактуются в принятой категорной модели как множества с разбиениями, переходами сообщества из одних состояний в другие, удовлетворяющими этим требованиям, являются инъективные, сюръективные, не всюду определенные и не функциональные морфизмы структуры множеств с разбиениями. Будем искать стационарное конечное состояние сообщества, установившееся с течением времени. Такой ситуации отвечает следующая модификация экстремального принципа:
осуществляется состояние AÎ
ObFSi,s, для которого энтропия H![]() (A) максимальна при заданных внешних ресурсных ограничениях.
(A) максимальна при заданных внешних ресурсных ограничениях.
Пусть ni — численность организма вида i в сообществе; ![]() =(n
=(n![]() ,n
,n![]() ,...,nw) — вектор численностей; n=
,...,nw) — вектор численностей; n=![]() ni — полная численность организмов; Lk — количество в окружающей среде k-го ресурса; q
ni — полная численность организмов; Lk — количество в окружающей среде k-го ресурса; q![]() — потребность особи вида i в k-ом ресурсе. Очевидно, любое допустимое состояние сообщества полностью характеризуется вектором
— потребность особи вида i в k-ом ресурсе. Очевидно, любое допустимое состояние сообщества полностью характеризуется вектором ![]() . Можно показать [14], что J
. Можно показать [14], что J![]() (A)=
(A)=![]() , где A соответствует
, где A соответствует ![]() . С другой стороны, мы знаем из раздела 3, что J
. С другой стороны, мы знаем из раздела 3, что J![]() (A)=nn. Таким образом, возникает задача на условный экстремум [19]:
(A)=nn. Таким образом, возникает задача на условный экстремум [19]:
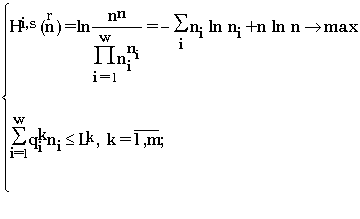
Решение этой задачи дается формулой видовой структуры [19, 20]:
ni =n exp(
-связывающей численности ni видов в экологическом сообществе с ресурсами Lk, от которых зависят n и l k. В работах [20,21,22] продемонстрирована адекватность формулы видовой структуры эмпирическим данным (см. также [23]).
Также показано, что:
решение экстремальной задачи существует и единственно при любых Lk>0 (k=![]() ) и осуществляет максимум функционала (теоремы существования и единственности) [19];
) и осуществляет максимум функционала (теоремы существования и единственности) [19];
пространство потребляемых сообществом ресурсов среды распадается (стратифицируется) на 2m-1 непересекающихся подмножеств, каждому из которых соответствует единственный набор потребляемых полностью ресурсов, и от тех же ресурсов как от аргументов и только от них в этих подмножествах зависит состояние сообщества ![]() (теорема стратификации) [19].
(теорема стратификации) [19].
Относительные численности видов зависят только от отношений количеств ресурсов в среде и принимают наибольшее значение при отношениях ресурсов, равных отношению потребностей в них для данного вида (теорема оптимизации) [24]. Теорема оптимизации порождает результативный метод управления видовой стуктурой экологических сообществ с помощью потоков ресурсных факторов среды [25,26,27].
Литература:
1. N.Rashevsky, “Topology and life. In search of general mathematical principles in biology and sociology”. Bull.Math.Biophys., 16, 1954, pp.317-348.
2. N.Rashevsky, “The geometrization in biology”. Bull.Math.Biophys., 17, 1955, pp.31-56.
3. N.Rashevsky,“Some remarks on topological biology”. Bull.Math.Biophys., 17, 1955, pp.207-218.
4. N.Rashevsky, “Life, information theory and topology”. Bull.Math.Biophys., 17, 1955, pp.229-235.
5. R.Rosen, “A relational theory of biological systems”. Bull.Math.Biophys., 20, 1958, pp.245-260.
6. R.Rosen,“The representation of biological systems from the standpoint of the theory of categories”. Bull.Math.Biophys., 20, 1958, pp.317-342.
7. R.Rosen, “A relational theory of biological systems. II”. Bull.Math.Biophys., 21, 1959, pp.109-127.
8. A.F.Bartholomay, “Molecular set theory. A mathematical representation for chemical reaction mechanisms”. Bull.Math.Biophys., 22, 1960, pp.285-307.
9. A.F.Bartholomay, “Molecular set theory. II. An aspect of biomathematical theory of sets”. Bull.Math.Biophys., 27, 1965, pp.235-251.
10. J. Baianu, M.Marinescu, “Organismic supercategories. I. Proposals for a general unitary theory of systems”. Bull.Math.Biophys., v., 30, 1968, pp.625-635.
11. J.Baianu, “Organismic supercategories. II. On multistable systems”. Bull.Math.Biophys., 32, 1970, pp.539-561.
12. C.A.Leguizamon, “Concept of energy in biological systems. A theory for environmental systems”. Bull.Math.Biol., 37, 1975, pp.565-572, 675-689.
13. C.A.Leguizamon, “The periodic continuous effect in terms of the algebraic relational theory”. Journal of Biological Systems, 1, 1993, pp.1-25.
14. А.П.Левич, “Теория множеств, язык теории категорий и их применение в теоретической биологии”. М.: Изд-во МГУ, 1982.
15. Н.Бурбаки, “Теория множеств”. М.: Мир, 1965
16. И.Букур, А.Деляну, “Введение в теорию категорий и функторов”. М.: Мир, 1972.
17. Р.Голдблатт, “Топосы. Категорный анализ логики”. М.: Мир, 1983.
18. А.П.Левич, “Информация как структура систем”. Семиотика и информатика, N 10, 1978, с.116-132.
19. А.П.Левич, В.Л.Алексеев, В.А.Никулин, “Математические аспекты вариационного моделирования в экологии сообществ”. Математическое моделирование, 1994, Т.6. N 5. С.55-76.
20. А.П.Левич, “Структура экологических сообществ”. М.: Изд-во МГУ, 1980.
21. А.П.Левич, Е.Д.Любимова, Г.Ш.Марташвили, ”Видовая стуктура и потребление субстратно-энергетических факторов в лабораторных альгоценозах”. Экологический прогноз. М.: Изд-во МГУ, 1986. С.69-103.
22. А.П.Левич, Д.Г.Замолодчиков, С.Ю.Рыбакова, “Исследование адекватности теоретико-категорной модели фитопланктонных сообществ”. Проблемы экологического мониторинга и моделирование в экологии. Л.: Гидрометеоиздат, 15., 1993.
23. D.Lurie, J.Valls, J.Vagensberg, “Thermodynamic approach to biomass distribution in ecological systems”. Bull.Math.Biol., 45, No 5, 1983, pp.869-872.
24. А.П.Левич, В.Л.Алексеев, С.Ю.Рыбакова, “Оптимизация структуры экологических сообществ: модельный анализ”. Биофизика, 38, N 5, 1993, с.877-885.
25. А.П.Левич, Н.Г.Булгаков, “О возможности регулирования видовой структуры лабораторного альгоценоза”. Известия РАН, N 4, 1993, с.569-578.
26. А.П.Левич, А.А.Худоян, Н.Г.Булгаков, В.И.Артюхова, “О возможности управления видовой и размерной структурами сообщества в экспериментах с природным фитопланктоном in vitro”. Биологические науки, N 7, 1992, с.17-31.
27. A.P.Levich, N.G.Bulgakov, “Regulation of species and size composition in phytoplankton communities in situ by N:P ratio”. Russian Journal of Aquatic Ecology, No 2, 1992, pp.149-159.