|
Постановка вопроса о "природе времени и сущности жизни" с реляционной точки зрения требует разграничения участвующих здесь категорий, которые отражают разные уровни сложности в едином методологическом подходе. В такой реляционной методологии нет специальных субстанций, отвечающих за течение времени или проявление жизни. Здесь делается попытка построить единую статистическую модель, где в иерархической последовательности воспроизводились бы важнейшие природные проявления, в частности, времени и биологических объектов. Но понятие "время" находится здесь на гораздо более высоком и общем уровне описания (и в силу этого более универсальном и простом), чем понятие "жизнь". Построение моделей времени, в том числе "необратимого" и "неравновесного", само по себе не исчерпывает биологических свойств, хотя и является, быть может, необходимым условием для адекватного описания.
Ранее была предложена статистическая модель времени (Аристов,1989). В этой работе внимание было в основном сосредоточено на изучении метрических свойств времени и построении математической модели часов, из которой следуют уравнения движения механики, но смысл вводимой модели шире. Время здесь не является отвлеченным параметром, но выступает в качестве характеристики самой системы. Поэтому для любого объекта (в том числе и биологического) может рассматриваться свое внутреннее время, и на его основе статистическим образом может строиться характеристика движения – определяться ход внутренних часов. Кратко опишем основные положения модели. Пусть задана система из 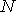 частиц. Будем считать, что имеется декартова система координат (т.е. пространство определено) и есть прибор "фотоаппарат", с помощью которого можно получать данные ("фотографии") о пространственном положении всех частиц системы. Одно мгновение вводимого времени будет теперь характеризоваться не одним параметром, а частиц. Будем считать, что имеется декартова система координат (т.е. пространство определено) и есть прибор "фотоаппарат", с помощью которого можно получать данные ("фотографии") о пространственном положении всех частиц системы. Одно мгновение вводимого времени будет теперь характеризоваться не одним параметром, а 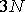 параметрами : точкой в параметрами : точкой в 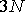 -мерном конфигурационном пространстве -мерном конфигурационном пространстве 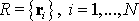 . Имея только одну эту "фотографию", можно ее занумеровать числом 1. Будем считать, что получая еще одну "фотографию", мы увидим отличия в положении некоторых частиц (здесь содержится предположение о движении, но нет предположения о времени или о упорядоченности событий во времени). Присвоим новой фотографии номер 2. Мы получили два момента упорядоченного многопараметрического "времени". Подчеркнем, что указанным образом упорядочивая моменты (хранящийся в памяти имеет меньший номер), мы пытаемся строить "время" в согласии с общепринятым, но неявным образом действий Если бы хранящемуся в памяти образу приписывался больший номер, то была бы построена иная модель времени. Для характеристики величины протекшего "времени" между двумя мгновениями может быть введена та или иная метрика (это будет по сути математической моделью часов). Для получения обратимого времени механики интервал времени между бесконечно близкими событиями вводится так: . Имея только одну эту "фотографию", можно ее занумеровать числом 1. Будем считать, что получая еще одну "фотографию", мы увидим отличия в положении некоторых частиц (здесь содержится предположение о движении, но нет предположения о времени или о упорядоченности событий во времени). Присвоим новой фотографии номер 2. Мы получили два момента упорядоченного многопараметрического "времени". Подчеркнем, что указанным образом упорядочивая моменты (хранящийся в памяти имеет меньший номер), мы пытаемся строить "время" в согласии с общепринятым, но неявным образом действий Если бы хранящемуся в памяти образу приписывался больший номер, то была бы построена иная модель времени. Для характеристики величины протекшего "времени" между двумя мгновениями может быть введена та или иная метрика (это будет по сути математической моделью часов). Для получения обратимого времени механики интервал времени между бесконечно близкими событиями вводится так:
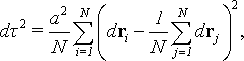 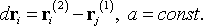 |
(1) |
Отсюда удается получить аналоги законов сохранения и другие положения классической механики. Важно подчеркнуть, что в формуле (1) очень большая информация о состоянии системы сведена к одному временному параметру. Для того чтобы удовлетворить (1), необязательно следить за каждой частицей - важно лишь, чтобы получалась та же самая среднеквадратичная сумма. Но подробное слежение за системой, где считается, что каждая частица (здесь не оговаривается, что понимается под этим понятием) может быть идентифицируема, приводит к понятию необратимого времени. Действительно, если движение частиц происходит сколько-нибудь случайным образом, то чрезвычайно маловероятно, что какая-то "фотография", характеризующаяся множеством параметров, полностью совпадет с другой фотографией. В этом смысле каждый момент так введенного "времени" уникален, и "время" необратимо, оно имеет определенную "стрелу". Но связана ли она непосредственно со "стрелой жизни" (если можно так выразиться) в биологических системах? С точки зрения реляционного подхода, биологическая "стрела" связана с необратимостью процессов, а не с "необратимостью времени" в указанном выше более широком смысле. Можно попытаться усложнить модель возможного времени и часов, сузив область приложения. Можно постараться определить "неравновесное" время, которое совпадало бы с вышеописанным "равновесным" только при тепловом равновесии в системе. Выделим p групп частиц; пусть каждая из этих групп частиц поддерживается в однородных условиях. Определим интервал "неравновесного" времени так:
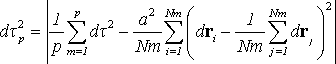 , , 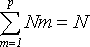 , ,
где d? определяется из (1). Величина  может быть качественно сопоставлена с
может быть качественно сопоставлена с 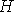 -функцией: в неравновесном состоянии -функцией: в неравновесном состоянии 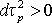 , в равновесии , в равновесии 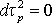 . Но более тонкие определения различных "времен" могут дать только дополнительные необходимые (но не достаточные) условия для описания биологических систем. Представляется, что специфичность биологических объектов должна быть выявлена с помощью более сложных постановок задач для уравнений все более высокого уровня. Таким образом, "время" есть более общее понятие, "на фоне" которого разворачиваются сложные биологические события; в рамках рассматриваемой статистической модели биологический объект оказывается вложенным в систему "времен" все большей общности. Есть и внутреннее время именно этого объекта, но выявление его еще недостаточно, чтобы подчеркнуть специфику живого. . Но более тонкие определения различных "времен" могут дать только дополнительные необходимые (но не достаточные) условия для описания биологических систем. Представляется, что специфичность биологических объектов должна быть выявлена с помощью более сложных постановок задач для уравнений все более высокого уровня. Таким образом, "время" есть более общее понятие, "на фоне" которого разворачиваются сложные биологические события; в рамках рассматриваемой статистической модели биологический объект оказывается вложенным в систему "времен" все большей общности. Есть и внутреннее время именно этого объекта, но выявление его еще недостаточно, чтобы подчеркнуть специфику живого.
Представляется, что в качестве указанного уравнения более высокого уровня может выступать кинетическое уравнение Больцмана (известен интерес к нему, поскольку в этом уравнении принцип энтропии выводится как теорема), но математическая сложность долго не позволяла решать его. Оно имеет вид:
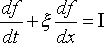 , ,
С целью построить простую модель сильно неравновесной открытой системы, "питающейся отрицательной энтропией" (что является важнейшим признаком живого по Бауэру и Шредингеру), для этого необратимого во времени уравнения была поставлена одномерная задача стационарной неоднородной релаксации (Aristov, 1991). Слева на границе полубесконечной области 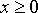 задается стационарная неравновесная функция распределения для втекающих в область частиц (для отрицательных скоростей функция распределения мала). При сносе в положительном направлении происходит релаксация, образуется неоднородная стационарная структура макропараметров, особый интерес представляет энтропия. От сильно неравновесной граничной функции энтропия (
задается стационарная неравновесная функция распределения для втекающих в область частиц (для отрицательных скоростей функция распределения мала). При сносе в положительном направлении происходит релаксация, образуется неоднородная стационарная структура макропараметров, особый интерес представляет энтропия. От сильно неравновесной граничной функции энтропия (  ) растет до равновесного значения. Интеграл по пространству от полученной неравновесной энтропии меньше, чем если бы в каждой точке было локальное равновесие. Тем самым может быть придан смысл утверждению о "низкоэнтропийности" биосистем, которое подвергается сомнению в работах различных авторов (Блюменфельд, 1977). Но был также обнаружен следующий существенный факт: при некоторых граничных условиях профиль энтропии имеет максимум и, если ставить граничное условие в точке максимума, то ниже по течению энтропия будет только уменьшаться. Естественно, это не противоречит Н-теореме. В обозначениях (Пригожин, 1986) имеем для стационарной открытой системы: ) растет до равновесного значения. Интеграл по пространству от полученной неравновесной энтропии меньше, чем если бы в каждой точке было локальное равновесие. Тем самым может быть придан смысл утверждению о "низкоэнтропийности" биосистем, которое подвергается сомнению в работах различных авторов (Блюменфельд, 1977). Но был также обнаружен следующий существенный факт: при некоторых граничных условиях профиль энтропии имеет максимум и, если ставить граничное условие в точке максимума, то ниже по течению энтропия будет только уменьшаться. Естественно, это не противоречит Н-теореме. В обозначениях (Пригожин, 1986) имеем для стационарной открытой системы:
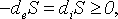 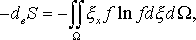 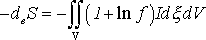
Это равенство является следствием уравнения Больцмана. Поток энтропии 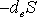 вовне положителен, но сама энтропия на выходе может оказаться меньше, чем на входе, как показал указанный пример. Т.е. открытая система может быть источником (вовне) отрицательной энтропии (правда, эта величина в построенном примере не превышала нескольких процентов). Описанная простая модель позволяет сделать выводы о допустимых размерах живой системы, некоторые утверждения качественно соотносятся с экспериментальными данными (Шмидт-Ниельсен, 1987). Эта модель также позволяет сделать вывод о характерном времени "старения" данной системы, которое значительно больше времени релаксации. Делается вывод о том, что "старение" — это проявление изолированности системы на большом масштабе времени. Для того чтобы "управлять" этим характерным временем, надо сделать систему более открытой — гипотетически можно представить кооперацию живых организмов, замену клеток на более молодые и т.д.
вовне положителен, но сама энтропия на выходе может оказаться меньше, чем на входе, как показал указанный пример. Т.е. открытая система может быть источником (вовне) отрицательной энтропии (правда, эта величина в построенном примере не превышала нескольких процентов). Описанная простая модель позволяет сделать выводы о допустимых размерах живой системы, некоторые утверждения качественно соотносятся с экспериментальными данными (Шмидт-Ниельсен, 1987). Эта модель также позволяет сделать вывод о характерном времени "старения" данной системы, которое значительно больше времени релаксации. Делается вывод о том, что "старение" — это проявление изолированности системы на большом масштабе времени. Для того чтобы "управлять" этим характерным временем, надо сделать систему более открытой — гипотетически можно представить кооперацию живых организмов, замену клеток на более молодые и т.д.
Литература
- АРИСТОВ В.В. Время, связанное со статистической моделью часов. Рукопись депонирована в ВИНИТИ. №7596-В89 от 19.12.89. M. 1989. 28с.
- БЛЮМЕНФЕЛЬД Л.А. Проблемы биологической физики. М.: Наука.1978. 336 с.
- ПРИГОЖИН И. От существующего к возникающему. М.: Наука.1985.327с.
- ШМИДТ-НИЕЛЬСЕН К. Размеры животных: почему они так важны? M.: Мир. 1987. 259с.
- ARISTOV V. Development of the regular method of solution of the Boltzmann equation and nonuniform relaxation problems // Proceed 17-th Internat. Symp. On Rarefied Gas Dynamics (Aachen 1990). Weinheim, ed. A. Beylich. 1991. P. 879-885.
|
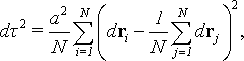
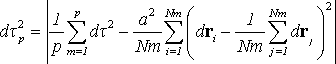 ,
,